Difference between revisions of "Aufgaben:Exercise 4.2: Mismatched Line"
| Line 66: | Line 66: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | '''(1)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | ||
| − | *Der Wellenwiderstand $Z_{\rm W}$ ist definiert als der Quotient von Spannung und Strom der sich entlang der Leitung ausbreitenden Welle | + | *Der Wellenwiderstand $Z_{\rm W}$ ist definiert als der Quotient von Spannung und Strom der sich entlang der Leitung ausbreitenden Welle. |
| + | *Der Wellenwiderstand $Z_{\rm W}$ unabhängig vom Ort. | ||
*Deshalb ist $Z_{\rm W}$ auch unabhängig von der Leitungslänge $l$ und wird allein durch die Leitungsbeläge $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.05cm}'$ und $C\hspace{0.05cm}'$ bestimmt. | *Deshalb ist $Z_{\rm W}$ auch unabhängig von der Leitungslänge $l$ und wird allein durch die Leitungsbeläge $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.05cm}'$ und $C\hspace{0.05cm}'$ bestimmt. | ||
*Die im Theorieteil angegebene Gleichung | *Die im Theorieteil angegebene Gleichung | ||
| Line 73: | Line 74: | ||
macht deutlich, dass der Wellenwiderstand durchaus von der Frequenz abhängt und im allgemeinen auch komplexwertig ist. | macht deutlich, dass der Wellenwiderstand durchaus von der Frequenz abhängt und im allgemeinen auch komplexwertig ist. | ||
| − | + | Anzumerken ist, dass der Wellenwiderstand kein Widerstand im Sinne eines Verbrauchers ist: | |
*Der Wellenwiderstand charakterisiert die Leitung nicht als verlustbehaftetes Element. | *Der Wellenwiderstand charakterisiert die Leitung nicht als verlustbehaftetes Element. | ||
| − | *Auch eine verlustlose Leitung besitzt einen Wellenwiderstand | + | *Auch eine verlustlose Leitung besitzt einen Wellenwiderstand. |
| + | *Ebenso ist bei der Ausbreitung einer elektromagnetischen Welle stets ein Wellenwiderstand definiert. | ||
| + | |||
| Line 85: | Line 88: | ||
Z_{\rm W}(f) \hspace{0.05cm}.$$ | Z_{\rm W}(f) \hspace{0.05cm}.$$ | ||
Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u>: | Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u>: | ||
| − | *Da in der Aufgabenstellung $Z_{\rm W}(f) = Z_{\rm W}$ als frequenzunabhängig vorausgesetzt wurde, ist | + | *Da in der Aufgabenstellung $Z_{\rm W}(f) = Z_{\rm W}$ als frequenzunabhängig vorausgesetzt wurde, ist auch der Eingangswiderstand $Z_{\rm E}(f) = Z_{\rm E}$ frequenzunabhängig. |
| − | *Dagegen können bei frequenzabhängigem Wellenwiderstand mit reellem Abschluss | + | *Dagegen können bei frequenzabhängigem Wellenwiderstand mit reellem Abschluss nicht für alle Frequenzen Reflexionen vermieden werden. |
| − | *Die Beschaltung $R_1 = R_2 =Z_{\rm W}$ ⇒ $R_1 =Z_{\rm E}$ ist | + | *Die Beschaltung $R_1 = R_2 =Z_{\rm W}$ ⇒ $R_1 =Z_{\rm E}$ ist anzustreben, da dann von der Quelle die maximale Leistung abgegeben wird. |
| + | |||
| Line 106: | Line 110: | ||
Das heißt: | Das heißt: | ||
*Bei der Frequenz $f_{\rm O} = 40\ {\rm MHz}$ genügt bereits die Leitungslänge $l= 2.65 \ \rm km$, um Reflexionen weitgehend zu unterdrücken. | *Bei der Frequenz $f_{\rm O} = 40\ {\rm MHz}$ genügt bereits die Leitungslänge $l= 2.65 \ \rm km$, um Reflexionen weitgehend zu unterdrücken. | ||
| − | *Bei | + | *Bei niedrigerer Frequenz $f_{\rm U} = 10\ {\rm MHz}$ ist wegen des geringeren Dämpfungsmaßes eine größere Kabellänge erforderlich. |
*Diese Aussagen beziehen sich natürlich nur auf das Vermeiden von Reflexionen. | *Diese Aussagen beziehen sich natürlich nur auf das Vermeiden von Reflexionen. | ||
*Insgesamt ist natürlich die niedrigere Signalfrequenz günstiger als die höhere. | *Insgesamt ist natürlich die niedrigere Signalfrequenz günstiger als die höhere. | ||
| + | |||
| Line 114: | Line 119: | ||
:$$\frac{Z_{\rm E}(f)}{Z_{\rm W}} = \frac{1}{{\rm tanh}(x)} | :$$\frac{Z_{\rm E}(f)}{Z_{\rm W}} = \frac{1}{{\rm tanh}(x)} | ||
= \frac {{\rm e}^{2x}+1}{{\rm e}^{2x}-1}\hspace{0.05cm}.$$ | = \frac {{\rm e}^{2x}+1}{{\rm e}^{2x}-1}\hspace{0.05cm}.$$ | ||
| − | Im Gegensatz zum Kurzschluss–Fall ergibt sich für den Quotienten $Z_{\rm E}/Z_{\rm W}$ | + | Im Gegensatz zum Kurzschluss–Fall ergibt sich nun für den Quotienten $Z_{\rm E}/Z_{\rm W} > 1$: |
:$${Z_{\rm E}(f)}/{Z_{\rm W}} = 1.01 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$${Z_{\rm E}(f)}/{Z_{\rm W}} = 1.01 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
{\rm e}^{2x} = 201\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | {\rm e}^{2x} = 201\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 120: | Line 125: | ||
Näherungsweise erhält man hier das gleiche Ergebnis wie bei Teilaufgabe (3): | Näherungsweise erhält man hier das gleiche Ergebnis wie bei Teilaufgabe (3): | ||
*Bei der Frequenz $f_{\rm O} = 40\ {\rm MHz}$ genügt bereits die Leitungslänge $l= 2.65 \ \rm km$, um Reflexionen weitgehend zu unterdrücken. | *Bei der Frequenz $f_{\rm O} = 40\ {\rm MHz}$ genügt bereits die Leitungslänge $l= 2.65 \ \rm km$, um Reflexionen weitgehend zu unterdrücken. | ||
| − | *Bei der niedrigeren Frequenz $f_{\rm U} = 10\ {\rm MHz}$ ist wegen des geringeren Dämpfungsmaßes | + | *Bei der niedrigeren Frequenz $f_{\rm U} = 10\ {\rm MHz}$ ist wegen des geringeren Dämpfungsmaßes eine größere Kabellänge erforderlich. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 16:25, 28 November 2018
Ein Übertragungssystem belege den Bereich von $f_{\rm U} = 10 \ \rm MHz$ bis $f_{\rm O} = 400 \ \rm MHz$.
Die verwendete Übertragungsleitung besitze zudem einen konstanten Wellenwiderstand $Z_{\rm W} = 100 \ \rm \Omega$ (reell), was nicht ganz der Realität entspricht, da der Wellenwiderstand meist mit der Frequenz leicht abnimmt und oft auch noch ein (meist kleinerer) Imaginärteil zu berücksichtigen ist.
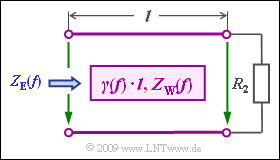
Die Leitung wird mit einer Spannungsquelle mit dem Innenwiderstand $R_{\rm 1} = 100 \ \rm \Omega$ gespeist und ist mit dem Widerstand $R_{\rm 2}$ abgeschlossen. Der Eingangswiderstand der Leitung ergibt sich zu
- $$Z_{\rm E}(f) = Z_{\rm W}\cdot \frac {R_2 + Z_{\rm W} \cdot {\rm tanh}(\gamma(f) \cdot l)} {Z_{\rm W}+ R_2 \cdot {\rm tanh}(\gamma(f) \cdot l)} \hspace{0.05cm},\hspace{0.3cm}{\rm tanh}(x) = \frac {{\rm e}^{x}-{\rm e}^{-x}}{{\rm e}^{x}+{\rm e}^{-x}}\hspace{0.05cm}, \hspace{0.3cm}x \in {\cal C} \hspace{0.05cm}.$$
Das Übertragungsmaß soll – wieder sehr vereinfacht – durch eine reelle Funktion angenähert werden:
- $$\frac {\gamma(f)}{1\,{\rm Np/km}} = \frac {\alpha(f)}{1\,{\rm Np/km}} = \sqrt{f/f_{\rm O}} \hspace{0.05cm}, \hspace{0.3cm}f_{\rm O} = 40\,{\rm MHz}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Ergebnisse der Leitungstheorie.
- Insbesondere soll untersucht werden, ob es zu Reflexionen kommt.
Fragebogen
Musterlösung
- Der Wellenwiderstand $Z_{\rm W}$ ist definiert als der Quotient von Spannung und Strom der sich entlang der Leitung ausbreitenden Welle.
- Der Wellenwiderstand $Z_{\rm W}$ unabhängig vom Ort.
- Deshalb ist $Z_{\rm W}$ auch unabhängig von der Leitungslänge $l$ und wird allein durch die Leitungsbeläge $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.05cm}'$ und $C\hspace{0.05cm}'$ bestimmt.
- Die im Theorieteil angegebene Gleichung
- $$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.05cm}' + {\rm j} \cdot \omega L\hspace{0.05cm}'}{G\hspace{0.05cm}' + {\rm j} \cdot \omega C\hspace{0.05cm}'}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm} \omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}$$
macht deutlich, dass der Wellenwiderstand durchaus von der Frequenz abhängt und im allgemeinen auch komplexwertig ist.
Anzumerken ist, dass der Wellenwiderstand kein Widerstand im Sinne eines Verbrauchers ist:
- Der Wellenwiderstand charakterisiert die Leitung nicht als verlustbehaftetes Element.
- Auch eine verlustlose Leitung besitzt einen Wellenwiderstand.
- Ebenso ist bei der Ausbreitung einer elektromagnetischen Welle stets ein Wellenwiderstand definiert.
(2) Mit dem Abschlusswiderstand $Z_{\rm 2}(f) = Z_{\rm W}(f)$ ist auch der an den Leitungsanfang transformierte Widerstandswert gleich dem Wellenwiderstand, und zwar unabhängig von der Leitungslänge:
- $$Z_{\rm E}(f) = Z_{\rm W}(f)\cdot \frac {Z_{\rm 2}(f) + Z_{\rm W}(f) \cdot {\rm tanh}(\gamma(f) \cdot l)} {Z_{\rm W}(f)+ Z_{\rm 2}(f) \cdot {\rm tanh}(\gamma(f) \cdot l)}= Z_{\rm W}(f)\cdot \frac {Z_{\rm W}(f) + Z_{\rm W}(f) \cdot {\rm tanh}(\gamma(f) \cdot l)} {Z_{\rm W}(f)+ Z_{\rm W}(f) \cdot {\rm tanh}(\gamma(f) \cdot l)}= Z_{\rm W}(f) \hspace{0.05cm}.$$
Richtig sind die Lösungsvorschläge 1, 2 und 4:
- Da in der Aufgabenstellung $Z_{\rm W}(f) = Z_{\rm W}$ als frequenzunabhängig vorausgesetzt wurde, ist auch der Eingangswiderstand $Z_{\rm E}(f) = Z_{\rm E}$ frequenzunabhängig.
- Dagegen können bei frequenzabhängigem Wellenwiderstand mit reellem Abschluss nicht für alle Frequenzen Reflexionen vermieden werden.
- Die Beschaltung $R_1 = R_2 =Z_{\rm W}$ ⇒ $R_1 =Z_{\rm E}$ ist anzustreben, da dann von der Quelle die maximale Leistung abgegeben wird.
(3) Mit dem Abschlusswiderstand $R_{\rm 2} = 0$ ⇒ Kurzschluss folgt aus der angegebenen Gleichung mit reellem $x = \gamma (f) \cdot l$:
- $$\frac{Z_{\rm E}(f)}{Z_{\rm W}} = {\rm tanh}(x) = \frac {{\rm e}^{x}-{\rm e}^{-x}}{{\rm e}^{x}+{\rm e}^{-x}}= \frac {{\rm e}^{2x}-1}{{\rm e}^{2x}+1}.$$
Insbesondere gilt:
- $${Z_{\rm E}(f)}/{Z_{\rm W}} = 0.99 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm e}^{2x} = 199\hspace{0.3cm}\Rightarrow \hspace{0.3cm} x ={1}/{2}\cdot {\rm ln}\hspace{0.1cm}(199) \approx 2.65\,{\rm Np}\hspace{0.05cm}.$$
- $$f_{\rm U} = 10\,\text {MHz:}\hspace{0.2cm}\alpha(f_{\rm U})= 0.5\,{\rm Np/km}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}l_{\rm min}= \frac{2.65\,{\rm Np}}{0.5\,{\rm Np/km}}\hspace{0.15cm}\underline{= 5.3\,{\rm km}} \hspace{0.05cm},$$
- $$ f_{\rm O} = 40\,\text {MHz:}\hspace{0.2cm}\alpha(f_{\rm U})= 1.0\,{\rm Np/km}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}l_{\rm min}= \frac{2.65\,{\rm Np}}{1.0\,{\rm Np/km}}\hspace{0.15cm}\underline{= 2.65\,{\rm km}} \hspace{0.05cm}.$$
Das heißt:
- Bei der Frequenz $f_{\rm O} = 40\ {\rm MHz}$ genügt bereits die Leitungslänge $l= 2.65 \ \rm km$, um Reflexionen weitgehend zu unterdrücken.
- Bei niedrigerer Frequenz $f_{\rm U} = 10\ {\rm MHz}$ ist wegen des geringeren Dämpfungsmaßes eine größere Kabellänge erforderlich.
- Diese Aussagen beziehen sich natürlich nur auf das Vermeiden von Reflexionen.
- Insgesamt ist natürlich die niedrigere Signalfrequenz günstiger als die höhere.
(4) In gleicher Weise erhält man für $R_2 → ∞$ ⇒ Leerlauf die Gleichung
- $$\frac{Z_{\rm E}(f)}{Z_{\rm W}} = \frac{1}{{\rm tanh}(x)} = \frac {{\rm e}^{2x}+1}{{\rm e}^{2x}-1}\hspace{0.05cm}.$$
Im Gegensatz zum Kurzschluss–Fall ergibt sich nun für den Quotienten $Z_{\rm E}/Z_{\rm W} > 1$:
- $${Z_{\rm E}(f)}/{Z_{\rm W}} = 1.01 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm e}^{2x} = 201\hspace{0.3cm}\Rightarrow \hspace{0.3cm} x ={1}/{2}\cdot{\rm ln}\hspace{0.1cm}(201) \approx 2.65\,{\rm Np}\hspace{0.05cm}.$$
Näherungsweise erhält man hier das gleiche Ergebnis wie bei Teilaufgabe (3):
- Bei der Frequenz $f_{\rm O} = 40\ {\rm MHz}$ genügt bereits die Leitungslänge $l= 2.65 \ \rm km$, um Reflexionen weitgehend zu unterdrücken.
- Bei der niedrigeren Frequenz $f_{\rm U} = 10\ {\rm MHz}$ ist wegen des geringeren Dämpfungsmaßes eine größere Kabellänge erforderlich.