Difference between revisions of "Aufgaben:Exercise 1.3: Rectangular Functions for Transmitter and Receiver"
| Line 2: | Line 2: | ||
}} | }} | ||
| − | [[File: P_ID1267__Dig_A_1_3.png|right|frame| | + | [[File: P_ID1267__Dig_A_1_3.png|right|frame|Drei verschiedene Systemkonzepte]] |
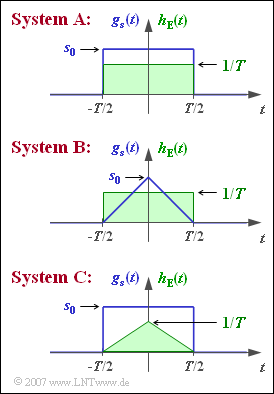
Wir betrachten hier drei Varianten eines binären bipolaren AWGN–Übertragungssystems, die sich hinsichtlich des Sendegrundimpulses $g_{s}(t)$ sowie der Impulsantwort $h_{\rm E}(t)$ des Empfangsfilters unterscheiden: | Wir betrachten hier drei Varianten eines binären bipolaren AWGN–Übertragungssystems, die sich hinsichtlich des Sendegrundimpulses $g_{s}(t)$ sowie der Impulsantwort $h_{\rm E}(t)$ des Empfangsfilters unterscheiden: | ||
*Beim $\text{System A}$ sind sowohl $g_{s}(t)$ als auch $h_{\rm E}(t)$ rechteckförmig, lediglich die Impulshöhen $(s_{\rm 0}$ bzw. $1/T)$ sind unterschiedlich. | *Beim $\text{System A}$ sind sowohl $g_{s}(t)$ als auch $h_{\rm E}(t)$ rechteckförmig, lediglich die Impulshöhen $(s_{\rm 0}$ bzw. $1/T)$ sind unterschiedlich. | ||
| Line 31: | Line 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie für | + | {Berechnen Sie für $\text{System A}$ den Detektionsgrundimpuls $g_{d}(t) = g_{ s}(t) \star h_{\rm E}(t)$. <br>Welcher Wert $g_0 = g_{d}(t=0)$ ergibt sich zum Zeitpunkt $t = 0$? |
|type="{}"} | |type="{}"} | ||
$g_0 \hspace{0.28cm} = \ $ { 6 3% } $\ \rm W^{1/2}$ | $g_0 \hspace{0.28cm} = \ $ { 6 3% } $\ \rm W^{1/2}$ | ||
| − | {Berechnen Sie daraus die Detektionsstörleistung $σ_{ | + | {Berechnen Sie daraus die Detektionsstörleistung $σ_{d}^2$. |
|type="{}"} | |type="{}"} | ||
$σ_{d}^{\hspace{0.02cm}2} \hspace{0.2cm} = \ $ { 1 3% } $\ \rm W$ | $σ_{d}^{\hspace{0.02cm}2} \hspace{0.2cm} = \ $ { 1 3% } $\ \rm W$ | ||
| − | {Welche Bitfehlerwahrscheinlichkeit $p_{\rm B}$ ergibt sich somit für das System A? | + | {Welche Bitfehlerwahrscheinlichkeit $p_{\rm B}$ ergibt sich somit für das $\text{System A}$? |
|type="{}"} | |type="{}"} | ||
$p_{\rm B} \hspace{0.2cm} = \ $ { 0.987 10% } $\ \cdot 10^{-9}$ | $p_{\rm B} \hspace{0.2cm} = \ $ { 0.987 10% } $\ \cdot 10^{-9}$ | ||
| − | {Ermitteln Sie die entsprechenden Größen für | + | {Ermitteln Sie die entsprechenden Größen für das $\text{System B}$ . |
|type="{}"} | |type="{}"} | ||
$g_0 \hspace{0.28cm} = \ $ { 3 3% } $\ \rm W^{1/2}$ | $g_0 \hspace{0.28cm} = \ $ { 3 3% } $\ \rm W^{1/2}$ | ||
| Line 49: | Line 49: | ||
$p_{\rm B} \hspace{0.2cm} = \ $ { 0.135 10% } $\ \cdot 10^{-2}$ | $p_{\rm B} \hspace{0.2cm} = \ $ { 0.135 10% } $\ \cdot 10^{-2}$ | ||
| − | {Wie lauten die Kenngrößen für das | + | {Wie lauten die Kenngrößen für das $\text{System C}$ ? |
|type="{}"} | |type="{}"} | ||
$g_0 \hspace{0.28cm} = \ $ { 3 3% } $\ \rm W^{1/2}$ | $g_0 \hspace{0.28cm} = \ $ { 3 3% } $\ \rm W^{1/2}$ | ||
Revision as of 12:51, 30 January 2019
Wir betrachten hier drei Varianten eines binären bipolaren AWGN–Übertragungssystems, die sich hinsichtlich des Sendegrundimpulses $g_{s}(t)$ sowie der Impulsantwort $h_{\rm E}(t)$ des Empfangsfilters unterscheiden:
- Beim $\text{System A}$ sind sowohl $g_{s}(t)$ als auch $h_{\rm E}(t)$ rechteckförmig, lediglich die Impulshöhen $(s_{\rm 0}$ bzw. $1/T)$ sind unterschiedlich.
- Das $\text{System B}$ unterscheidet sich vom $\text{System A}$ durch einen dreieckförmigen Sendegrundimpuls mit $g_{s}(t=0) = s_{\rm 0}$.
- Das $\text{System C}$ hat den gleichen Sendegrundimpuls wie $\text{System A}$, während die Impulsantwort mit $h_{\rm E}(t=0) = 1/T$ dreieckförmig verläuft.
Die absolute Breite der hier betrachteten Rechteck– und Dreieckfunktionen beträgt jeweils $T = 10 \ \rm µ s$. Die Bitrate ist $R = 100 \ \rm kbit/s$. Die weiteren Systemparameter sind wie folgt gegeben:
- $$s_0 = 6 \,\,\sqrt{W}\hspace{0.05cm},\hspace{0.3cm} N_{\rm 0} = 2 \cdot 10^{-5} \,\,{\rm W/Hz}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Fehlerwahrscheinlichkeit bei Basisbandübertragung.
- Zur Bestimmung von Fehlerwahrscheinlichkeiten können Sie das interaktive Applet Komplementäre Gaußsche Fehlerfunktionen verwenden.
- Berücksichtigen Sie bei der Berechnung der Detektionsstörleistung das Theorem von Wiener–Chintchine:
- $$ \sigma _d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H_{\rm E}( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {h_{\rm E}( t )} \right|^2 \hspace{0.1cm}{\rm{d}}t}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$g_d (t = 0) = \int_{ - T/2}^{ + T/2} { g_s(t) \cdot h_{\rm E}( t )} \hspace{0.1cm}{\rm{d}}t =s_0 \cdot \frac{1 }{T} \cdot T = s_0 \hspace{0.1cm}\underline { = 6 \,\,\sqrt{{\rm W}}}\hspace{0.05cm}.$$
Es gibt keine Impulsinterferenzen, da für $| t |\ge T$ der Detektionsimpuls $g_{d}(t) = 0$ ist.
2. Die Varianz des Detektionsstörsignals – hier als Detektionsstörleistung bezeichnet – kann sowohl im Zeit– als auch im Frequenzbereich berechnet werden. Bei der vorliegenden Rechteckform führt die Berechnung im Zeitbereich schneller zum Ergebnis:
- $$\sigma _d ^2 \ = \ \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {h_{\rm E}( t )} \right|^2 \hspace{0.1cm}{\rm{d}}t} =\frac{N_0 }{2} \cdot \int_{ - T/2 }^{ + T/2 } {\left| {h_{\rm E}( t )} \right|^2 \hspace{0.1cm}{\rm{d}}t} = \ \frac{N_0 }{2} \cdot\frac{1 }{T^2} \cdot T = \frac{N_0 }{2T} = \frac{2 \cdot 10^{-5} \,\,{\rm W/Hz}}{2 \cdot 10^{-5} \,\,{\rm s}} \hspace{0.1cm}\underline {= 1\,{\rm W}}\hspace{0.05cm}.$$
Die Frequenzbereichsberechnung würde mit $H_{\rm E}(f) = {\rm si}(πfT)$ wie folgt aussehen:
- $$\sigma _d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H_{\rm E}( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = \frac{N_0 }{2} \cdot \int_{- \infty }^{ \infty } {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm{d}}f = \frac{N_0 }{2T} \hspace{0.05cm}.$$
3. Aufgrund der zeitlich begrenzten Impulsform (das bedeutet: keine Impulsinterferenzen!) ergibt sich bei der hier vorausgesetzten bipolaren Betrachtungsweise:
- $$p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)= {\rm Q} \left( \frac{ 6 \,\sqrt{\rm W}}{1 \,\sqrt{\rm W}}\right) = {\rm Q}(6) \hspace{0.1cm}\underline {= 0.987 \cdot 10^{-9}} \hspace{0.05cm}.$$
System A stellt die Matched–Filter–Realisierung des optimalen Binärempfängers dar, so dass auch folgende Gleichungen anwendbar wären:
- $$E_{\rm B} = s_0^2 \cdot T = 36\, {\rm W} \cdot 10^{-5} {\rm s}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0}}\right) ={\rm Q} \left( \sqrt{\frac{2 \cdot 36 \cdot 10^{-5}\,\, {\rm Ws}}{2 \cdot 10^{-5} \,\, {\rm Ws}}}\right)={\rm Q}(6) \hspace{0.05cm}.$$
4. Da bei System B das gleiche Empfangsfilter wie bei System A verwendet wird, erhält man auch die gleiche Detektionsstörleistung $σ_{d}^2 = 1 \ \rm W$. Der Detektionsgrundimpuls ist nun aber nicht mehr dreieckförmig, sondern weist eine spitzere Form auf. Zum Zeitpunkt $t = 0$ gilt:
- $$g_d (t = 0) = \frac{1}{T} \cdot \int_{ - T/2}^{ + T/2} { g_s(t) } \hspace{0.1cm}{\rm{d}}t = \frac{1}{T} \cdot \frac{s_0 }{2} \cdot T = \frac{s_0 }{2}\hspace{0.1cm}\underline {= 3 \,\,\sqrt{\rm W}}\hspace{0.05cm}.$$
Auch das System B ist impulsinterferenzfrei. Man erhält deshalb für die Bitfehlerwahrscheinlichkeit:
- $$p_{\rm B} = {\rm Q} \left( \frac{g_d (t = 0)}{\sigma_d}\right)= {\rm Q} \left( \frac{ 3 \,\sqrt{\rm W}}{1 \,\sqrt{\rm W}}\right) = {\rm Q}(3) \hspace{0.1cm}\underline {= 0.135 \cdot 10^{-2}} \hspace{0.05cm}.$$
Nicht anwendbar ist dagegen hier der folgende Rechengang:
- $$E_{\rm B} = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t = 2\cdot s_0^2 \cdot \int ^{+T/2} _{0} \left( 1- \frac{2t}{T}\right)^2\,{\rm d}t = \frac{s_0^2 \cdot T }{3} = 12 \cdot 10^{-5} \,{\rm Ws}$$
- $$\Rightarrow \hspace{0.3cm} p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0}}\right) ={\rm Q} \left( \sqrt{12}\right)={\rm Q}(3.464) \approx 3 \cdot 10^{-4} \hspace{0.05cm}.$$
Man würde so eine zu niedrige Bitfehlerwahrscheinlichkeit berechnen, da die implizit getroffene Annahme eines angepassten Filters nicht zutrifft.
5. Bei rechteckförmigem Sendegrundimpuls und dreieckförmiger Impulsantwort ⇒ System C erhält man den gleichen Detektionsgrundimpuls wie bei dreieckförmigem $g_{\rm s}(t)$ und rechteckförmigem $h_{\rm E}(t)$. Wie beim System B gilt deshalb:
- $$g_d (t = 0) = \frac{s_0}{2}\hspace{0.1cm}\underline {= 3 \,\,\sqrt{\rm W}}\hspace{0.05cm}.$$
Dagegen ist nun die Detektionsstörleistung kleiner als bei den Systemen A und B:
- $$\sigma _d ^2 = \frac{N_0}{2} \cdot \frac{1}{T^2} \cdot \int^{+T/2} _{-T/2} \left( 1- \frac{2t}{T}\right)^2\,{\rm d}t = \frac{N_0}{6T}\hspace{0.1cm}\underline { = 0.333 \,{\rm W}}.$$
Damit erhält man nun für die Bitfehlerwahrscheinlichkeit:
- $$p_{\rm B} = {\rm Q} \left( \frac{ 3 \,\sqrt{\rm W}}{0.577 \,\sqrt{\rm W}}\right) \approx {\rm Q}(5.2)\hspace{0.1cm}\underline { \approx 10^{-7} } \hspace{0.05cm}.$$
Der gegenüber Teilfrage (3) erkennbare Anstieg der Fehlerwahrscheinlichkeit um etwa den Faktor $100$ ist auf die gravierende Fehlanpassung gegenüber dem Matched–Filter zurückzuführen. Die Verbesserung gegenüber Teilaufgabe (4) geht auf die höhere Signalenergie zurück.