Difference between revisions of "Digital Signal Transmission/Error Probability with Intersymbol Interference"
| Line 182: | Line 182: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Als eine sehr einfache Näherung für die tatsächliche Fehlerwahrscheinlichkeit $p_{\rm S}$ | + | $\text{Definition:}$ Als eine sehr einfache Näherung für die tatsächliche Fehlerwahrscheinlichkeit $p_{\rm S}$ |
| − | verwendet man häufig die '''ungünstigste Fehlerwahrscheinlichkeit''' (englisch: <i>Worst-Case Error Probability</i>) | + | verwendet man häufig die '''ungünstigste Fehlerwahrscheinlichkeit''' (englisch: <i>Worst-Case Error Probability</i>) |
[[File:P ID1379 Dig T 3 2 S4 version1.png|right|frame|Zusammenhang zwischen mittlerer und ungünstigster Fehlerwahrscheinlichkeit|class=fit]] | [[File:P ID1379 Dig T 3 2 S4 version1.png|right|frame|Zusammenhang zwischen mittlerer und ungünstigster Fehlerwahrscheinlichkeit|class=fit]] | ||
:$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} | :$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} | ||
\right) \hspace{0.05cm}.$$ | \right) \hspace{0.05cm}.$$ | ||
| − | + | Für deren Berechnung wird stets von den ungünstigsten Symbolfolgen ausgegangen. Das bedeutet: | |
| + | *Die tatsächliche WDF der Nutzabtastwerte (linke Grafik: sechs rote Diracs) wird durch eine vereinfachte WDF mit nur den inneren Diracfunktionen (rechte Grafik: zwei grüne Diracs) ersetzt.<br> | ||
| − | + | *Für die halbe vertikale Augenöffnung gilt mit den Grundimpulswerten $g_\nu = g_d( T_{\rm D}+ \nu \cdot T)$ allgemein: | |
| − | |||
| − | |||
| − | *Für die halbe vertikale Augenöffnung gilt mit den Grundimpulswerten $g_\nu = g_d( T_{\rm D}+ \nu \cdot T)$ allgemein: | ||
:$$\ddot{o}(T_{\rm D})/{ 2}= g_0 - \sum_{\nu = 1}^{n} \vert g_{\nu} \vert- \sum_{\nu = 1}^{v} \vert g_{-\nu} \vert \hspace{0.05cm}.$$}} | :$$\ddot{o}(T_{\rm D})/{ 2}= g_0 - \sum_{\nu = 1}^{n} \vert g_{\nu} \vert- \sum_{\nu = 1}^{v} \vert g_{-\nu} \vert \hspace{0.05cm}.$$}} | ||
Diese Gleichung kann wie folgt interpretiert werden: | Diese Gleichung kann wie folgt interpretiert werden: | ||
| − | *$g_0 = g_d( T_{\rm D})$ ist der so genannte ''Hauptwert'' des Grundimpulses. Bei Nyquistsystemen gilt stets $\ddot{o}(T_{\rm D})/{ 2}= g_0$. Im Folgenden wird (meist) $T_{\rm D}= 0$ gesetzt.<br> | + | *$g_0 = g_d( T_{\rm D})$ ist der so genannte ''Hauptwert'' des Grundimpulses. Bei Nyquistsystemen gilt stets $\ddot{o}(T_{\rm D})/{ 2}= g_0$. Im Folgenden wird (meist) $T_{\rm D}= 0$ gesetzt.<br> |
| − | *Die erste Summe beschreibt die Impulsinterferenzen der $n$ ''Nachläufer'' vorangegangener Impulse. Stillschweigend vorausgesetzt wird $g_\nu = 0$ für $\nu \gt n$.<br> | + | *Die erste Summe beschreibt die Impulsinterferenzen der $n$ ''Nachläufer'' vorangegangener Impulse. Stillschweigend vorausgesetzt wird $g_\nu = 0$ für $\nu \gt n$.<br> |
| − | *Die zweite Summe berücksichtigt den Einfluss der $v$ ''Vorläufer'' nachfolgender Impulse unter der Voraussetzung $g_{-\nu} = 0$ für $\nu \gt v$.<br> | + | *Die zweite Summe berücksichtigt den Einfluss der $v$ ''Vorläufer'' nachfolgender Impulse unter der Voraussetzung $g_{-\nu} = 0$ für $\nu \gt v$.<br> |
| − | *Sind alle Impulsvor– und –nachläufer positiv, so lauten die beiden ungünstigsten Symbolfolgen „$\text{...}\hspace{0.05cm} -\hspace{-0.1cm}1,\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} -\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$” und „$\text{...}\hspace{0.05cm} +\hspace{-0.1cm}1,\hspace{0.05cm} +\hspace{-0.05cm}1,\hspace{0.05cm} {\it -\hspace{-0.05cm}1},\hspace{0.05cm} +\hspace{-0.05cm}1,\hspace{0.05cm} +\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$” (Koeffizient $a_{\nu = 0}$ kursiv). | + | *Sind alle Impulsvor– und –nachläufer positiv, so lauten die beiden ungünstigsten Symbolfolgen „$\text{...}\hspace{0.05cm} -\hspace{-0.1cm}1,\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} -\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$” und „$\text{...}\hspace{0.05cm} +\hspace{-0.1cm}1,\hspace{0.05cm} +\hspace{-0.05cm}1,\hspace{0.05cm} {\it -\hspace{-0.05cm}1},\hspace{0.05cm} +\hspace{-0.05cm}1,\hspace{0.05cm} +\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$” (der Koeffizient $a_{\nu = 0}$ ist jeweils kursiv). Diese Angaben treffen zum Beispiel für das hier betrachtete gaußförmige Empfangsfilter zu.<br> |
*Sind einige Grundimpulswerte negativ, so wird dies in obiger Gleichung durch die Betragsbildung berücksichtigt. Es ergeben sich dann andere „Worst–Case”–Folgen als gerade genannt.<br> | *Sind einige Grundimpulswerte negativ, so wird dies in obiger Gleichung durch die Betragsbildung berücksichtigt. Es ergeben sich dann andere „Worst–Case”–Folgen als gerade genannt.<br> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 5:}$ Die Grafik zeigt die Fehlerwahrscheinlichkeiten des AWGN–Kanals in Abhängigkeit des Quotienten $E_{\rm B}/N_0$, nämlich | + | $\text{Beispiel 5:}$ Die Grafik zeigt die Fehlerwahrscheinlichkeiten des AWGN–Kanals in Abhängigkeit des (logarithmierten) Quotienten $E_{\rm B}/N_0$, nämlich |
| − | *die mittlere Fehlerwahrscheinlichkeit $p_{\rm S}$ bei gaußförmigem Empfangsfilter (blaue Kreise),<br> | + | *die mittlere Fehlerwahrscheinlichkeit $p_{\rm S}$ bei gaußförmigem Empfangsfilter (blaue Kreise),<br> |
| − | *die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ bei gaußförmigem Empfangsfilter (blaue Rechtecke),<br> | + | *die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ bei gaußförmigem Empfangsfilter (blaue Rechtecke),<br> |
| − | *die kleinstmögliche Fehlerwahrscheinlichkeit gemäß der Seite [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Optimaler_Bin.C3.A4rempf.C3.A4nger_-_Realisierung_mit_Matched-Filter| Optimaler Binärempfänger]] (rote Kurve).<br><br> | + | *die kleinstmögliche Fehlerwahrscheinlichkeit gemäß der Seite [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Optimaler_Bin.C3.A4rempf.C3.A4nger_-_Realisierung_mit_Matched-Filter| Optimaler Binärempfänger]] (rote Kurve).<br><br> |
| − | Die Energie pro Bit ist dabei gleich $E_{\rm B} = s_0^2 \cdot T$ (NRZ–Rechteck–Sendeimpulse).<br> | + | Die Energie pro Bit ist dabei gleich $E_{\rm B} = s_0^2 \cdot T$ (NRZ–Rechteck–Sendeimpulse).<br> |
| − | [[File:P ID1385 Dig T 3 2 S4b version2.png|center|frame|Mittlere und ungünstigste Fehlerwahrscheinlichkeit vs. | + | [[File:P ID1385 Dig T 3 2 S4b version2.png|center|frame|Mittlere und ungünstigste Fehlerwahrscheinlichkeit vs. $E_{\rm B}/N-0$|class=fit]]<br> |
| − | Die linke Grafik gilt für die (normierte) Grenzfrequenz $f_{\rm G} \cdot T = 0.4$, die rechte für ein breitbandigeres Empfangsfilter mit $f_{\rm G} \cdot T = 0.8$. | + | Die linke Grafik gilt für die (normierte) Grenzfrequenz $f_{\rm G} \cdot T = 0.4$, die rechte für ein breitbandigeres Empfangsfilter mit $f_{\rm G} \cdot T = 0.8$. Die Ergebnisse können wie folgt interpretiert werden: |
| − | *Die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ ist stets eine obere Schranke für die tatsächliche Symbolfehlerwahrscheinlichkeit $p_{\rm S}$. Je kleiner der Einfluss der Impulsinterferenzen ist (große Grenzfrequenz), um so näher liegen $p_{\rm S}$ und $p_{\rm U}$ zusammen. Beim Optimalempfänger gilt $p_{\rm S} = p_{\rm U}.$ | + | *Die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ ist stets eine obere Schranke für die tatsächliche Symbolfehlerwahrscheinlichkeit $p_{\rm S}$. Je kleiner der Einfluss der Impulsinterferenzen ist (große Grenzfrequenz), um so näher liegen $p_{\rm S}$ und $p_{\rm U}$ zusammen. Beim Optimalempfänger gilt $p_{\rm S} = p_{\rm U}.$ |
| − | *Bei gaußförmigem Empfangsfilter mit $f_{\rm G} \cdot T \ge 0.3$ werden die Impulsinterferenzen allein durch die Nachbarimpulse hervorgerufen $(g_2 = g_3 = \text{...} \approx 0)$, so dass für $p_{\rm S}$ auch eine untere Schranke angegeben werden kann: | + | *Bei gaußförmigem Empfangsfilter mit $f_{\rm G} \cdot T \ge 0.3$ werden die Impulsinterferenzen allein durch die Nachbarimpulse hervorgerufen $(g_2 = g_3 = \text{...} \approx 0)$, so dass für $p_{\rm S}$ auch eine untere Schranke angegeben werden kann: |
:$${p_{\rm U} }/{ 4} \le p_{\rm S} \le p_{\rm U} | :$${p_{\rm U} }/{ 4} \le p_{\rm S} \le p_{\rm U} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Die starken Impulsinterferenzen eines gaußförmigen Empfangsfilters mit $f_{\rm G} \cdot T = 0.4$ führen dazu, dass gegenüber dem Optimalempfänger ein um $6 \ \rm dB$ größeres $E_{\rm B}/N_0$ aufgewendet werden muss (vierfache Leistung), damit die Fehlerwahrscheinlichkeit den Wert $10^{-8}$ nicht überschreitet.<br> | + | *Die starken Impulsinterferenzen eines gaußförmigen Empfangsfilters mit $f_{\rm G} \cdot T = 0.4$ führen dazu, dass gegenüber dem Optimalempfänger ein um $6 \ \rm dB$ größeres $E_{\rm B}/N_0$ aufgewendet werden muss (vierfache Leistung), damit die Fehlerwahrscheinlichkeit den Wert $10^{-8}$ nicht überschreitet.<br> |
| − | *Der horizontale Abstand zwischen der blauen $p_{\rm S}$–Kurve (markiert durch Kreise) und der roten Vergleichskurve ist aber nicht konstant. Bei $p_{\rm S} = 10^{-2}$ beträgt der Abstand nur $4 \ \rm dB$.<br> | + | *Der horizontale Abstand zwischen der blauen $p_{\rm S}$–Kurve (markiert durch Kreise) und der roten Vergleichskurve ist aber nicht konstant. Bei $p_{\rm S} = 10^{-2}$ beträgt der Abstand nur $4 \ \rm dB$.<br> |
| − | *Die rechte Grafik zeigt, dass mit $f_{\rm G} \cdot T = 0.8$ der Abstand zum Vergleichssystem weniger als $1 \ \rm dB$ beträgt. Auf der nächsten Seite wird gezeigt, dass bei einem gaußförmigen Empfangsfilter die (normierte) Grenzfrequenz $f_{\rm G} \cdot T \approx 0.8$ das Optimum darstellt.}}<br> | + | *Die rechte Grafik zeigt, dass mit $f_{\rm G} \cdot T = 0.8$ der Abstand zum Vergleichssystem weniger als $1 \ \rm dB$ beträgt. Auf der nächsten Seite wird gezeigt, dass bei einem gaußförmigen Empfangsfilter die (normierte) Grenzfrequenz $f_{\rm G} \cdot T \approx 0.8$ das Optimum darstellt.}}<br> |
== Optimierung der Grenzfrequenz== | == Optimierung der Grenzfrequenz== | ||
| Line 229: | Line 227: | ||
[[File:P ID1380 Dig T 3 2 S5 version1.png|right|frame|SNR in Abhängigkeit der Grenzfrequenz eines Gaußtiefpasses|class=fit]] | [[File:P ID1380 Dig T 3 2 S5 version1.png|right|frame|SNR in Abhängigkeit der Grenzfrequenz eines Gaußtiefpasses|class=fit]] | ||
Für die Systemoptimierung und den Systemvergleich erweist es sich als zweckmäßig, | Für die Systemoptimierung und den Systemvergleich erweist es sich als zweckmäßig, | ||
| − | *anstelle der ''ungünstigsten Fehlerwahrscheinlichkeit'' $p_{\rm U}$ | + | *anstelle der ''ungünstigsten Fehlerwahrscheinlichkeit'' $p_{\rm U}$ |
| − | *das ''ungünstigste Signal–zu–Rausch–Leistungsverhältnis'' (S/N-Verhältnis) zu verwenden: | + | *das ''ungünstigste Signal–zu–Rausch–Leistungsverhältnis'' (S/N-Verhältnis) zu verwenden: |
:$$\rho_{\rm U} = [\ddot{o}(T_{\rm D})]^2/ \sigma_d^2.$$ | :$$\rho_{\rm U} = [\ddot{o}(T_{\rm D})]^2/ \sigma_d^2.$$ | ||
| Line 237: | Line 235: | ||
\right) \hspace{0.05cm}.$$ | \right) \hspace{0.05cm}.$$ | ||
| − | Die mittlere Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ kann formal über die Q–Funktion ebenfalls durch ein S/N–Verhältnis ausgedrückt werden: | + | Die mittlere Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ kann formal über die Q–Funktion ebenfalls durch ein S/N–Verhältnis ausgedrückt werden: |
:$$\rho_d = \left[{\rm Q}^{-1} \left( p_{\rm S} | :$$\rho_d = \left[{\rm Q}^{-1} \left( p_{\rm S} | ||
| Line 243: | Line 241: | ||
| − | Die Grafik zeigt die beiden Größen $\rho_d$ und $\rho_{\rm U}$ in logarithmischer Form abhängig von der normierten Grenzfrequenz $f_{\rm G} \cdot T | + | Die Grafik zeigt die beiden Größen $\rho_d$ und $\rho_{\rm U}$ in logarithmischer Form abhängig von der normierten Grenzfrequenz $f_{\rm G} \cdot T$ eines gaußförmigen Empfangsfilters, wobei $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 13 \ \rm dB$ zugrunde liegt. |
| − | *Die blau umrandeten Kreise gelten für $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d$ ⇒ „mittleres” Detektions–SNR,<br> | + | *Die blau umrandeten Kreise gelten für $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d$ ⇒ „mittleres” Detektions–SNR,<br> |
| − | *Die blau umrandeten Quadrate markieren $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U}$ ⇒ „ungünstigstes” SNR. | + | *Die blau umrandeten Quadrate markieren $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U}$ ⇒ „ungünstigstes” SNR. |
| − | Zum Vergleich ist als rote horizontale Linie auch das Ergebnis für den [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Optimaler_Bin.C3.A4rempf.C3.A4nger_-_Realisierung_mit_Matched-Filter| optimalen Binärempfänger]] eingezeichnet. Für diesen gilt: | + | Zum Vergleich ist als rote horizontale Linie auch das Ergebnis für den [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Optimaler_Bin.C3.A4rempf.C3.A4nger_-_Realisierung_mit_Matched-Filter| optimalen Binärempfänger]] eingezeichnet. Für diesen gilt: |
:$$\rho_d = \rho_{\rm U} = {2 \cdot E_{\rm B}}/{ N_0}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$\rho_d = \rho_{\rm U} = {2 \cdot E_{\rm B}}/{ N_0}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
10 \cdot {\rm lg}\hspace{0.1cm} \rho_d = 10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx 16\,{\rm dB} | 10 \cdot {\rm lg}\hspace{0.1cm} \rho_d = 10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx 16\,{\rm dB} | ||
| Line 254: | Line 252: | ||
Man erkennt aus der Darstellung: | Man erkennt aus der Darstellung: | ||
| − | *Das Optimierungskriterium $\rho_d$ führt zur optimalen Grenzfrequenz $f_\text{G, opt} \cdot T = 0.8$. Eine kleinere Grenzfrequenz hat stärkere Impulsinterferenzen zur Folge (kleinere Augenöffnung), eine größere Grenzfrequenz bewirkt einen größeren Rauscheffektivwert $\sigma_d$.<br> | + | *Das Optimierungskriterium $\rho_d$ führt zur optimalen Grenzfrequenz $f_\text{G, opt} \cdot T = 0.8$. Eine kleinere Grenzfrequenz hat stärkere Impulsinterferenzen zur Folge (kleinere Augenöffnung), eine größere Grenzfrequenz bewirkt einen größeren Rauscheffektivwert $\sigma_d$.<br> |
| − | *Ein solches gaußförmiges Empfangsfilter mit $f_\text{G, opt} \cdot T \approx 0.8$ führt zum Störabstand $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d \approx 15 \ \rm dB$ und damit zur Fehlerwahrscheinlichkeit $p_{\rm S} \approx 10^{-8}$. Zum Vergleich: Für den optimalen Empfänger (an den Sender angepasste Impulsantwort) ergeben sich $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d \approx 16 \ \rm dB$ und $p_{\rm S} \approx 10^{-10}$.<br> | + | *Ein solches gaußförmiges Empfangsfilter mit $f_\text{G, opt} \cdot T \approx 0.8$ führt zum Störabstand $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d \approx 15 \ \rm dB$ und damit zur Fehlerwahrscheinlichkeit $p_{\rm S} \approx 10^{-8}$. Zum Vergleich: Für den optimalen Empfänger (an den Sender angepasste Impulsantwort) ergeben sich $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d \approx 16 \ \rm dB$ und $p_{\rm S} \approx 10^{-10}$.<br> |
| − | *Die Grafik zeigt aber auch, dass das sehr viel einfachere Optimierungskriterien $ \rho_{\rm U}$ (bzw. $ p_{\rm U}$ | + | *Die Grafik zeigt aber auch, dass das sehr viel einfachere Optimierungskriterien $ \rho_{\rm U}$ $($bzw. $ p_{\rm U})$ näherungsweise zur gleichen optimalen Grenzfrequenz $f_\text{G, opt} \cdot T = 0.8$ führt. Für diese Grenzfrequenz erhält man $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx 14.7 \ \rm dB$ sowie die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} \approx 3 \cdot 10^{-8}$.<br> |
| − | *Ist die Grenzfrequenz $f_\text{G} \cdot T < 0.27$, so ergibt sich für die vertikale Augenöffnung immer $\ddot{o}(T_{\rm D}) = 0$. Man spricht von einem <i>geschlossenen Auge</i>. Dies hat zur Folge, dass einige ungünstige Impulsfolgen auch ohne Rauschen immer falsch entschieden würden. Es tritt ein systematischer Fehler auf.<br> | + | *Ist die Grenzfrequenz $f_\text{G} \cdot T < 0.27$, so ergibt sich für die vertikale Augenöffnung immer $\ddot{o}(T_{\rm D}) = 0$. Man spricht von einem <i>geschlossenen Auge</i>. Dies hat zur Folge, dass einige ungünstige Impulsfolgen auch ohne Rauschen immer falsch entschieden würden. Es tritt ein systematischer Fehler auf.<br> |
| − | *Weitere Untersuchungen haben gezeigt, dass das Optimierungskriterium $ \rho_{\rm U}$ auch bei kleinerem $E_{\rm B}/N_0$ ausreichend ist. Bei einem verzerrungsfreien Kanal ⇒ $H_{\rm K}(f) = 1$, ergibt sich somit die optimale Grenzfrequenz des Gaußtiefpasses stets zu $f_\text{G, opt} \cdot T \approx 0.8$, zumindest bei realitätsnaher Betrachtungsweise.<br><br> | + | *Weitere Untersuchungen haben gezeigt, dass das Optimierungskriterium $ \rho_{\rm U}$ auch bei kleinerem $E_{\rm B}/N_0$ ausreichend ist. Bei einem verzerrungsfreien Kanal ⇒ $H_{\rm K}(f) = 1$, ergibt sich somit die optimale Grenzfrequenz des Gaußtiefpasses stets zu $f_\text{G, opt} \cdot T \approx 0.8$, zumindest bei realitätsnaher Betrachtungsweise.<br><br> |
Alle Aussagen dieses Kapitels können mit dem interaktiven Applet [[Applets:Augendiagramm|Augendiagramm und Augenöffnung]] nachvollzogen werden. | Alle Aussagen dieses Kapitels können mit dem interaktiven Applet [[Applets:Augendiagramm|Augendiagramm und Augenöffnung]] nachvollzogen werden. | ||
Revision as of 17:52, 18 February 2019
Contents
Gaußförmiges Empfangsfilter
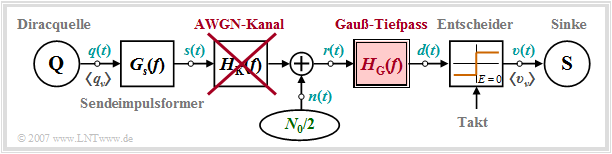
Wir gehen von dem skizzierten Blockschaltbild aus. Zur quantitativen Berücksichtigung der Impulsinterferenzen wird folgende Konfiguration angenommen:
- Rechteckförmiger NRZ–Sendegrundimpuls $g_s(t)$ mit der Höhe $s_0$ und der Dauer $T$,
- Gaußförmiges Empfangsfilter mit der Grenzfrequenz $f_{\rm G}$ (Hinweis: In diesem Abschnitt bezeichnen wir die Exponentialfunktion oft auch mit $\rm exp [ . ]$):
- $$H_{\rm E}(f) = H_{\rm G}(f) = {\rm exp}\left [- \frac{\pi \cdot f^2}{(2f_{\rm G})^2} \right ] \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.2cm}h_{\rm E}(t) = h_{\rm G}(t) = {\rm exp}\left [- \pi \cdot (2 f_{\rm G} t)^2\right ] \hspace{0.05cm}.$$
- AWGN–Kanal, das heißt, es gilt $H_{\rm K}(f) = 1 $ und ${\it \Phi}_n(f) = N_0/2$.
Aufgrund der hier getroffenen Voraussetzungen gilt für den Detektionsgrundimpuls:
- $$g_d(t) = g_s(t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot s_0 \cdot \int_{t-T/2}^{t+T/2} {\rm e}^{- \pi \hspace{0.05cm}\cdot\hspace{0.05cm} (2 \hspace{0.05cm}\cdot\hspace{0.05cm} f_{\rm G}\hspace{0.05cm}\cdot\hspace{0.05cm} \tau )^2} \,{\rm d} \tau \hspace{0.05cm}.$$
Die Integration führt zu folgenden äquivalenten Ergebnissen:
- $$g_d(t) = s_0 \cdot \big [ {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \big ],$$
- $$g_d(t) = s_0 \cdot\big [ {\rm erfc} \left ( 2 \cdot \sqrt {\pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm erfc} \left ( 2 \cdot \sqrt {\pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \big ]\hspace{0.05cm}.$$
Hierbei sind zwei Varianten der komplementären Gaußschen Fehlerfunktion verwendet, nämlich
- $${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d {\it u} \hspace{0.05cm},\hspace{0.5cm} {\rm erfc} (\it x) = \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.$$
Das Modul Komplementäre Gaußsche Fehlerfunktionen liefert die Zahlenwerte von ${\rm Q} (x)$ und $0.5 \cdot {\rm erfc} (x)$.
Die Rauschleistung am Ausgang des gaußförmigen Empfangsfilters $H_{\rm G}(f)$ ist gleich
- $$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0\cdot f_{\rm G}}{\sqrt{2}}\hspace{0.05cm}.$$
Aus diesen beiden Gleichungen erkennt man bereits:
- Je kleiner die Grenzfrequenz $f_{\rm G}$ des Gauß–Tiefpasses ist, desto kleiner ist der Rauscheffektivwert $\sigma_d$ und umso besser ist demzufolge das Rauschverhalten.
- Eine kleine Grenzfrequenz führt aber zu einer starken Abweichung des Detektionsgrundimpulses $g_d(t)$ von der Rechteckform und damit zu Impulsinterferenzen.
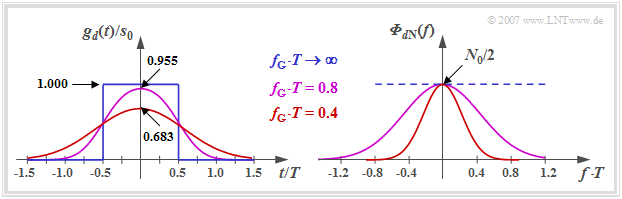
$\text{Beispiel 1:}$ Die linke Grafik zeigt den Detektionsgrundimpuls $g_d(t)$ am Ausgang eines Gaußtiefpasses $H_{\rm G}(f)$ mit der Grenzfrequenz $f_{\rm G}$, wenn am Eingang ein NRZ–Rechteckimpuls (blauer Kurvenverlauf) anliegt.
Man erkennt aus dieser Darstellung:
- Der Gaußtiefpass $H_{\rm G}(f)$ bewirkt, dass der Dektionsimpuls $g_d(t)$ gegenüber dem Sendeimpuls $g_s(t)$ verkleinert und verbreitert wird ⇒ Zeitdispersion.
- Diese Impulsverformung ist umso stärker, je kleiner die Grenzfrequenz $f_{\rm G}$ ist. Beispielsweise wird mit $f_{\rm G} \cdot T = 0.4$ (rote Kurve) das Impulsmaximum bereits auf etwa $68\%$ herabgesetzt.
- Im Grenzfall $f_{\rm G} \to \infty$ hat der Gaußtiefpass keine Wirkung ⇒ $g_d(t) = g_s(t)$. Allerdings ist in diesem Fall keinerlei Rauschbegrenzung wirksam, wie aus dem rechten Bild hervorgeht.
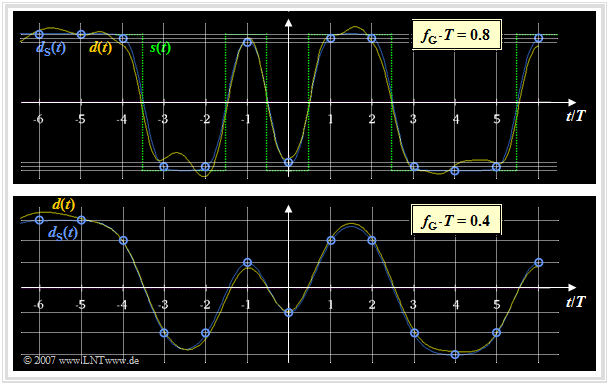
$\text{Beispiel 2:}$ Es gelten die gleichen Vorausetzungen wie für das letzte Beispiel. Die Grafik zeigt das Detektionssignal $d(t)$ nach dem Gaußtiefpass (vor dem Entscheider) für zwei verschiedene Grenzfrequenzen, nämlich $f_{\rm G} \cdot T = 0.8$ und $f_{\rm G} \cdot T = 0.4$
Dargestellt sind in beiden Diagrammen gleichermaßen (aber als Bildschirmabzug zugegebenermaßen schwer zu erkennen):
- der Anteil $d_{\rm S}(\nu \cdot T)$ ohne Berücksichtigung des Rauschens (blaue Kreise bei den Detektionszeitpunkten),
- das gesamte Detektionssignal $d(t)$ inklusive der Rauschkomponente (gelb),
- das Sendesignal $s(t)$ als Referenzsignal (grün gepunktet in der oberen Grafik; gleichermaßen gültig für die untere Grafik).
Durch einen Vergleich dieser Bilder lassen sich folgende Aussagen verifizieren:
- Mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.8$ (obere Grafik) ergeben sich zu den Detektionszeitpunkten $($bei Vielfachen von $T)$ nur geringfügige Impulsinterferenzen. Durch den Gaußtiefpass werden hier in erster Linie die Ecken des Sendesignals $s(t)$ abgerundet.
- Dagegen sind im unteren Bild $(f_{\rm G} \cdot T = 0.4)$ die Auswirkungen der Impulsinterferenzen deutlich zu erkennen. Zu den Detektionszeitpunkten $(\nu \cdot T)$ kann das blau dargestellte Detektionsnutzsignal $d_{\rm S}(\nu \cdot T)$ sechs verschiedene Werte annehmen (eingezeichnete Rasterlinien).
- Der Rauschanteil $d_{\rm N}(t)$ – erkennbar als Differenz zwischen der gelben Kurve und den blauen Kreisen – ist mit $f_{\rm G} \cdot T = 0.8$ im statistischen Mittel größer als mit $f_{\rm G} \cdot T = 0.4$.
- Dieses Ergebnis kann mit der der rechten Grafik von $\text{Beispiel 1}$ erklärt werden, die das Leistungsdichtespektrum der Rauschkomponente $d_{\rm N}(t)$ zeigt:
- $${\it \Phi}_{d{\rm N} }(f) = {N_0}/{2} \cdot \vert H_{\rm G}(f) \vert^2 = {N_0}/{2} \cdot {\rm exp}\left [- \frac{2\pi f^2}{(2f_{\rm G})^2} \right ] .$$
- Das Integral über ${\it \Phi}_{d{\rm N} }(f)$ – also die Rauschleistung $\sigma_d^2$ – ist für $f_{\rm G} \cdot T = 0.8$ (violette Kurve) doppelt so groß als mit $f_{\rm G} \cdot T = 0.4$ (rote Kurve).
Definition und Aussagen des Augendiagramms
Der oben dargelegte Sachverhalt lässt sich auch am Augendiagramm erklären.
$\text{Definition:}$ Unter dem Augendiagramm (Englisch: Eye Pattern) versteht man die Summe aller übereinander gezeichneten Ausschnitte des Detektionssignals, deren Dauer ein ganzzahliges Vielfaches der Symboldauer $T$ ist.
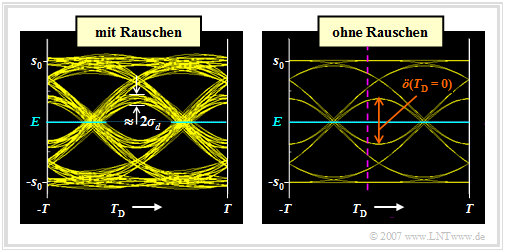
$\text{Beispiel 3:}$ Wir gehen von einem redundanzfreien binären bipolaren NRZ–Rechtecksignal $s(t)$ und dem Gaußtiefpass mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.4$ aus.
Dargestellt sind die Augendiagramme nach dem Gaußtiefpass,
- links mit Berücksichtigung des Rauschens ⇒ Signal $d(t)$,
- rechts ohne Berücksichtigung des Rauschens ⇒ Signal $d_{\rm S}(t)$.
Dieses Diagramm hat eine gewisse Ähnlichkeit mit einem Auge, was zu seiner Namensgebung geführt hat.
Diese Darstellung erlaubt wichtige Aussagen über die Qualität eines digitalen Übertragungssystems:
- Nur das Augendiagramm des Signals $d(t)$ kann messtechnisch auf einem Oszilloskop dargestellt werden, das mit dem Taktsignal getriggert wird. Aus diesem Augendiagramm (linke Grafik) kann beispielsweise der Rauscheffektivwert $\sigma_d$ abgelesen – besser gesagt: abgeschätzt – werden.
- Das Augendiagramm ohne Rauschen (rechte Grafik) bezieht sich auf das Detektionsnutzsignal $d_{\rm S}(t)$ und kann nur mittels einer Rechnersimulation ermittelt werden. Für ein realisiertes System ist dieses Augendiagramm nicht darstellbar, da der Rauschanteil $d_{\rm N}(t)$ nicht eliminiert werden kann.
- Bei beiden Diagrammen wurden jeweils $2048$ Augenlinien gezeichnet. In der rechten Grafik sind jedoch nur $2^5 = 32$ Augenlinien unterscheidbar, da der vorliegende Detektionsgrundimpuls $g_d(t)$ auf den Zeitbereich $\vert t\vert \le 2T$ beschränkt ist (siehe Grafik im $\text{Beispiel 1}$ mit $f_{\rm G} \cdot T = 0.4$, rote Kurve).
- Die inneren Augenlinien bestimmen die vertikale Augenöffnung $\ddot{o}(T_{\rm D})$. Je kleiner diese ist, desto größer ist der Einfluss von Impulsinterferenzen. Bei einem (impulsinterferenzfreien) Nyquistsystem ist die vertikale Augenöffnung maximal. Normiert auf die Sendeamplitude gilt dann $\ddot{o}(T_{\rm D})/s_0 = 2$.
- Bei symmetrischem Grundimpuls ist der Detektionszeitpunkt $T_{\rm D} = 0$ optimal. Mit einem anderen Wert $($zum Beispiel $T_{\rm D} = T/10) $ wäre $\ddot{o}(T_{\rm D})$ etwas kleiner und damit die Fehlerwahrscheinlichkeit deutlich größer. Dieser Fall ist in der rechten Grafik durch die violett–gestrichelte Vertikale angedeutet.
Mittlere Fehlerwahrscheinlichkeit
Wir gehen wie bei den bisherigen Grafiken in diesem Kapitel von folgenden Voraussetzungen aus:
- NRZ–Rechtecke mit Amplitude $s_0$, AWGN–Rauschen mit $N_0$, wobei
- $$10 \cdot {\rm lg}\hspace{0.1cm} \frac{s_0^2 \cdot T}{N_0}\approx 13\,{\rm dB}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{N_0}{s_0^2 \cdot T} = 0.05\hspace{0.05cm}.$$
- Gaußförmiges Empfangsfilter mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.4$:
- $$\sigma_d^2 = \frac{(N_0 /T)\cdot (f_{\rm G}\cdot T)}{\sqrt{2}}= \frac{0.05 \cdot s_0^2\cdot0.4}{\sqrt{2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma_d = \sqrt{0.0141}\cdot s_0 \approx 0.119 \cdot s_0 \hspace{0.05cm}.$$
- Es gelte $g_d(\nu \cdot T) \approx 0$ für $|\nu| \ge 2$. Die anderen Detektionsgrundimpulswerte sind wie folgt gegeben:
- $$g_0 = g_d(t=0) \approx 0.68 \cdot s_0, \hspace{0.5cm}g_1 = g_d(t=T) \approx 0.16 \cdot s_0, \hspace{0.2cm} g_{-1} = g_d(t=-T) \approx 0.16 \cdot s_0\hspace{0.05cm}.$$
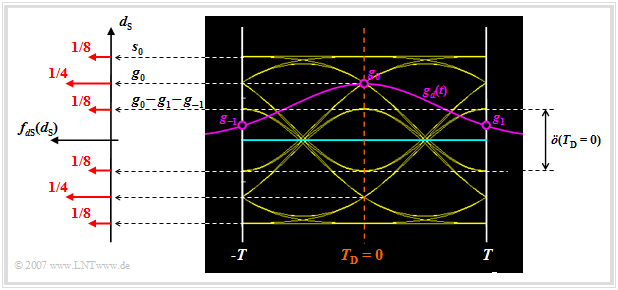
Analysieren wir nun die möglichen Werte für das Detektionsnutzsignal $d_{\rm S}(t)$ zu den Detektionszeitpunkten:
- Von den insgesamt $32$ Augenlinien schneiden vier Linien die Ordinate $(t = 0)$ bei $g_0 + 2 \cdot g_1 = s_0$. Diese Linien gehören zu den Amplitudenkoeffizienten „$\text{...}\hspace{0.05cm} +\hspace{-0.1cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} +\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$”. Kursiv hervorgehoben ist hierbei der „mittlere” Koeffizient $a_{\nu = 0}$.
- Die vier Augenlinien, die jeweils die Koeffizienten „$\text{...}\hspace{0.05cm} -\hspace{-0.1cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} \text{...}$” repräsentieren, ergeben den Nutzabtastwert $d_{\rm S}(T_{\rm D} = 0) =g_0 - 2 \cdot g_1 = 0.36 \cdot s_0$.
- Dagegen tritt der Nutzabtastwert $d_{\rm S}(T_{\rm D} = 0) =g_0 = 0.68 \cdot s_0$ doppelt so häufig auf. Dieser geht entweder auf die Koeffizienten „$\text{...}\hspace{0.05cm} +\hspace{-0.1cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$” oder auf „$\text{...}\hspace{0.05cm} -\hspace{-0.1cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} +\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$” zurück.
- Für die $16$ Augenlinien, welche die Ordinate $T_{\rm D} = 0$ unterhalb der Entscheiderschwelle $E = 0$ schneiden, ergeben sich genau spiegelbildliche Verhältnisse.
Die möglichen Werte $d_{\rm S}(T_{\rm D})$ und deren Auftrittswahrscheinlichkeiten findet man in obiger Grafik auf der linken Seite in der Wahrscheinlichkeitsdichtefunktion (WDF) der Detektionsnutzabtastwerte wieder:
- $$f_{d{\rm S}}(d_{\rm S}) = {1}/{8} \cdot \delta (d_{\rm S} - s_0)+ {1}/{4} \cdot \delta (d_{\rm S} - 0.68 \cdot s_0)+ {1}/{8} \cdot \delta (d_{\rm S} - 0.36 \cdot s_0)+ $$
$$\hspace{2.15cm} + \hspace{0.2cm} {1}/{8} \cdot \delta (d_{\rm S} + s_0)+{1}/{4} \cdot \delta (d_{\rm S} + 0.68 \cdot s_0)+{1}/{8} \cdot \delta (d_{\rm S} + 0.36 \cdot s_0)\hspace{0.05cm}.$$
Damit kann die (mittlere) Symbolfehlerwahrscheinlichkeit des impulsinterferenzbehafteten Systems angegeben werden. Unter Ausnutzung der Symmetrie erhält man mit $\sigma_d/s_0 = 0.119$:
- $$p_{\rm S} = {1}/{4} \cdot {\rm Q} \left( \frac{s_0}{ \sigma_d} \right)+ {1}/{2} \cdot {\rm Q} \left( \frac{0.68 \cdot s_0}{ \sigma_d} \right)+{1}/{4} \cdot {\rm Q} \left( \frac{0.36 \cdot s_0}{ \sigma_d} \right)$$
- $$\Rightarrow \hspace{0.3cm}p_{\rm S} \approx {1}/{4} \cdot {\rm Q}(8.40) +{1}/{2} \cdot {\rm Q}(5.71)+ {1}/{4} \cdot {\rm Q}(3.02)\approx {1}/{4} \cdot 2.20 \cdot 10^{-17}+ {1}/{2} \cdot 1.65 \cdot 10^{-9}+ {1}/{4} \cdot 1.26 \cdot 10^{-3} \approx 3.14 \cdot 10^{-4} \hspace{0.05cm}.$$
$\text{Fazit:}$ Anhand dieses Zahlenbeispiels erkennt man:
- Bei Vorhandensein von Impulsinterferenzen wird die (mittlere) Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ im Wesentlichen durch die inneren Augenlinien bestimmt.
- Der Rechenaufwand zur Bestimmung der Fehlerwahrscheinlichkeit $p_{\rm S}$ kann sehr groß werden, insbesondere dann, wenn die Impulsinterferenzen von sehr vielen Grundimpulswerten $g_\nu$ herrühren.
$\text{Beispiel 4:}$
- Sind die Grundimpulswerte $g_{-5}, \text{...} \ , g_{+5}$ von Null verschieden und $E \ne 0$, so ist zur Bestimmung der Fehlerwahrscheinlichkeit $p_{\rm S}$ eine Mittelung über $2^{11} = 2048$ Augenlinien erforderlich.
- Sind dagegen nur die Grundimpulswerte $g_{-1}, \ g_0, \ g_{+1}$ von Null verschieden und wird zudem die Symmetrie bezüglich der Schwelle $E = 0$ berücksichtigt, so reduziert sich der Aufwand auf die Mittelung über vier Terme.
- Gilt zusätzlich die Symmetrie $g_{-1} = g_{+1}$ wie bei den obigen Zahlenwerten, so kann auch die Symmetrie bezüglich $T_{\rm D}$ ausgenutzt werden und es genügt die Mittelung über drei Terme.
Ungünstigste Fehlerwahrscheinlichkeit
In der Vergangenheit wurden eine Vielzahl von Näherungen für die mittlere Fehlerwahrscheinlichkeit angegeben, unter Anderem:
$\text{Definition:}$ Als eine sehr einfache Näherung für die tatsächliche Fehlerwahrscheinlichkeit $p_{\rm S}$ verwendet man häufig die ungünstigste Fehlerwahrscheinlichkeit (englisch: Worst-Case Error Probability)
- $$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} \right) \hspace{0.05cm}.$$
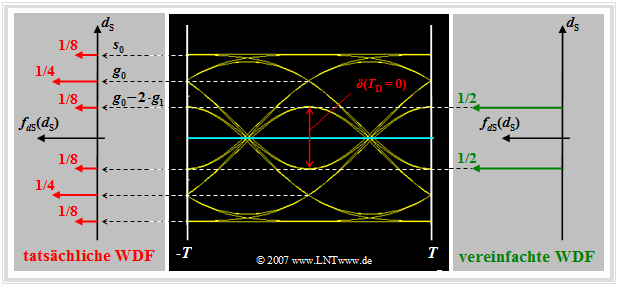
Für deren Berechnung wird stets von den ungünstigsten Symbolfolgen ausgegangen. Das bedeutet:
- Die tatsächliche WDF der Nutzabtastwerte (linke Grafik: sechs rote Diracs) wird durch eine vereinfachte WDF mit nur den inneren Diracfunktionen (rechte Grafik: zwei grüne Diracs) ersetzt.
- Für die halbe vertikale Augenöffnung gilt mit den Grundimpulswerten $g_\nu = g_d( T_{\rm D}+ \nu \cdot T)$ allgemein:
- $$\ddot{o}(T_{\rm D})/{ 2}= g_0 - \sum_{\nu = 1}^{n} \vert g_{\nu} \vert- \sum_{\nu = 1}^{v} \vert g_{-\nu} \vert \hspace{0.05cm}.$$
Diese Gleichung kann wie folgt interpretiert werden:
- $g_0 = g_d( T_{\rm D})$ ist der so genannte Hauptwert des Grundimpulses. Bei Nyquistsystemen gilt stets $\ddot{o}(T_{\rm D})/{ 2}= g_0$. Im Folgenden wird (meist) $T_{\rm D}= 0$ gesetzt.
- Die erste Summe beschreibt die Impulsinterferenzen der $n$ Nachläufer vorangegangener Impulse. Stillschweigend vorausgesetzt wird $g_\nu = 0$ für $\nu \gt n$.
- Die zweite Summe berücksichtigt den Einfluss der $v$ Vorläufer nachfolgender Impulse unter der Voraussetzung $g_{-\nu} = 0$ für $\nu \gt v$.
- Sind alle Impulsvor– und –nachläufer positiv, so lauten die beiden ungünstigsten Symbolfolgen „$\text{...}\hspace{0.05cm} -\hspace{-0.1cm}1,\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} -\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$” und „$\text{...}\hspace{0.05cm} +\hspace{-0.1cm}1,\hspace{0.05cm} +\hspace{-0.05cm}1,\hspace{0.05cm} {\it -\hspace{-0.05cm}1},\hspace{0.05cm} +\hspace{-0.05cm}1,\hspace{0.05cm} +\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$” (der Koeffizient $a_{\nu = 0}$ ist jeweils kursiv). Diese Angaben treffen zum Beispiel für das hier betrachtete gaußförmige Empfangsfilter zu.
- Sind einige Grundimpulswerte negativ, so wird dies in obiger Gleichung durch die Betragsbildung berücksichtigt. Es ergeben sich dann andere „Worst–Case”–Folgen als gerade genannt.
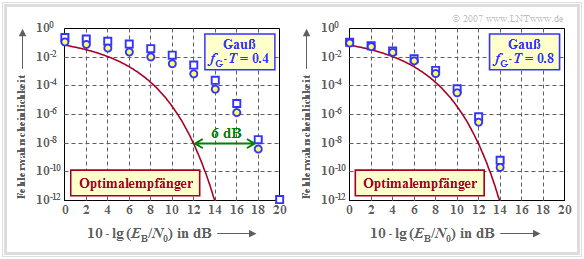
$\text{Beispiel 5:}$ Die Grafik zeigt die Fehlerwahrscheinlichkeiten des AWGN–Kanals in Abhängigkeit des (logarithmierten) Quotienten $E_{\rm B}/N_0$, nämlich
- die mittlere Fehlerwahrscheinlichkeit $p_{\rm S}$ bei gaußförmigem Empfangsfilter (blaue Kreise),
- die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ bei gaußförmigem Empfangsfilter (blaue Rechtecke),
- die kleinstmögliche Fehlerwahrscheinlichkeit gemäß der Seite Optimaler Binärempfänger (rote Kurve).
Die Energie pro Bit ist dabei gleich $E_{\rm B} = s_0^2 \cdot T$ (NRZ–Rechteck–Sendeimpulse).
Die linke Grafik gilt für die (normierte) Grenzfrequenz $f_{\rm G} \cdot T = 0.4$, die rechte für ein breitbandigeres Empfangsfilter mit $f_{\rm G} \cdot T = 0.8$. Die Ergebnisse können wie folgt interpretiert werden:
- Die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ ist stets eine obere Schranke für die tatsächliche Symbolfehlerwahrscheinlichkeit $p_{\rm S}$. Je kleiner der Einfluss der Impulsinterferenzen ist (große Grenzfrequenz), um so näher liegen $p_{\rm S}$ und $p_{\rm U}$ zusammen. Beim Optimalempfänger gilt $p_{\rm S} = p_{\rm U}.$
- Bei gaußförmigem Empfangsfilter mit $f_{\rm G} \cdot T \ge 0.3$ werden die Impulsinterferenzen allein durch die Nachbarimpulse hervorgerufen $(g_2 = g_3 = \text{...} \approx 0)$, so dass für $p_{\rm S}$ auch eine untere Schranke angegeben werden kann:
- $${p_{\rm U} }/{ 4} \le p_{\rm S} \le p_{\rm U} \hspace{0.05cm}.$$
- Die starken Impulsinterferenzen eines gaußförmigen Empfangsfilters mit $f_{\rm G} \cdot T = 0.4$ führen dazu, dass gegenüber dem Optimalempfänger ein um $6 \ \rm dB$ größeres $E_{\rm B}/N_0$ aufgewendet werden muss (vierfache Leistung), damit die Fehlerwahrscheinlichkeit den Wert $10^{-8}$ nicht überschreitet.
- Der horizontale Abstand zwischen der blauen $p_{\rm S}$–Kurve (markiert durch Kreise) und der roten Vergleichskurve ist aber nicht konstant. Bei $p_{\rm S} = 10^{-2}$ beträgt der Abstand nur $4 \ \rm dB$.
- Die rechte Grafik zeigt, dass mit $f_{\rm G} \cdot T = 0.8$ der Abstand zum Vergleichssystem weniger als $1 \ \rm dB$ beträgt. Auf der nächsten Seite wird gezeigt, dass bei einem gaußförmigen Empfangsfilter die (normierte) Grenzfrequenz $f_{\rm G} \cdot T \approx 0.8$ das Optimum darstellt.
Optimierung der Grenzfrequenz
Für die Systemoptimierung und den Systemvergleich erweist es sich als zweckmäßig,
- anstelle der ungünstigsten Fehlerwahrscheinlichkeit $p_{\rm U}$
- das ungünstigste Signal–zu–Rausch–Leistungsverhältnis (S/N-Verhältnis) zu verwenden:
- $$\rho_{\rm U} = [\ddot{o}(T_{\rm D})]^2/ \sigma_d^2.$$
Bei Gaußscher Störung besteht folgender Zusammenhang:
- $$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right) \hspace{0.05cm}.$$
Die mittlere Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ kann formal über die Q–Funktion ebenfalls durch ein S/N–Verhältnis ausgedrückt werden:
- $$\rho_d = \left[{\rm Q}^{-1} \left( p_{\rm S} \right)\right]^2 \hspace{0.05cm}.$$
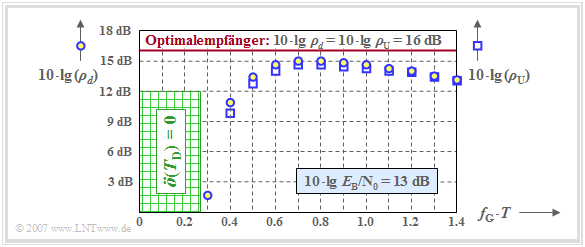
Die Grafik zeigt die beiden Größen $\rho_d$ und $\rho_{\rm U}$ in logarithmischer Form abhängig von der normierten Grenzfrequenz $f_{\rm G} \cdot T$ eines gaußförmigen Empfangsfilters, wobei $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 13 \ \rm dB$ zugrunde liegt.
- Die blau umrandeten Kreise gelten für $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d$ ⇒ „mittleres” Detektions–SNR,
- Die blau umrandeten Quadrate markieren $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U}$ ⇒ „ungünstigstes” SNR.
Zum Vergleich ist als rote horizontale Linie auch das Ergebnis für den optimalen Binärempfänger eingezeichnet. Für diesen gilt:
- $$\rho_d = \rho_{\rm U} = {2 \cdot E_{\rm B}}/{ N_0}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm} \rho_d = 10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx 16\,{\rm dB} \hspace{0.05cm}.$$
Man erkennt aus der Darstellung:
- Das Optimierungskriterium $\rho_d$ führt zur optimalen Grenzfrequenz $f_\text{G, opt} \cdot T = 0.8$. Eine kleinere Grenzfrequenz hat stärkere Impulsinterferenzen zur Folge (kleinere Augenöffnung), eine größere Grenzfrequenz bewirkt einen größeren Rauscheffektivwert $\sigma_d$.
- Ein solches gaußförmiges Empfangsfilter mit $f_\text{G, opt} \cdot T \approx 0.8$ führt zum Störabstand $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d \approx 15 \ \rm dB$ und damit zur Fehlerwahrscheinlichkeit $p_{\rm S} \approx 10^{-8}$. Zum Vergleich: Für den optimalen Empfänger (an den Sender angepasste Impulsantwort) ergeben sich $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d \approx 16 \ \rm dB$ und $p_{\rm S} \approx 10^{-10}$.
- Die Grafik zeigt aber auch, dass das sehr viel einfachere Optimierungskriterien $ \rho_{\rm U}$ $($bzw. $ p_{\rm U})$ näherungsweise zur gleichen optimalen Grenzfrequenz $f_\text{G, opt} \cdot T = 0.8$ führt. Für diese Grenzfrequenz erhält man $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx 14.7 \ \rm dB$ sowie die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} \approx 3 \cdot 10^{-8}$.
- Ist die Grenzfrequenz $f_\text{G} \cdot T < 0.27$, so ergibt sich für die vertikale Augenöffnung immer $\ddot{o}(T_{\rm D}) = 0$. Man spricht von einem geschlossenen Auge. Dies hat zur Folge, dass einige ungünstige Impulsfolgen auch ohne Rauschen immer falsch entschieden würden. Es tritt ein systematischer Fehler auf.
- Weitere Untersuchungen haben gezeigt, dass das Optimierungskriterium $ \rho_{\rm U}$ auch bei kleinerem $E_{\rm B}/N_0$ ausreichend ist. Bei einem verzerrungsfreien Kanal ⇒ $H_{\rm K}(f) = 1$, ergibt sich somit die optimale Grenzfrequenz des Gaußtiefpasses stets zu $f_\text{G, opt} \cdot T \approx 0.8$, zumindest bei realitätsnaher Betrachtungsweise.
Alle Aussagen dieses Kapitels können mit dem interaktiven Applet Augendiagramm und Augenöffnung nachvollzogen werden.
Aufgaben zum Kapitel
Aufgabe 3.2: Augendiagramm nach Gaußtiefpass
Aufgabe 3.2Z: Optimale Grenzfrequenz bei Gauß-Tiefpass