Difference between revisions of "Aufgaben:Exercise 4.08: Decision Regions at Three Symbols"
m (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | ||
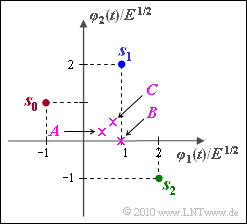
| − | [[File:P_ID2018__Dig_A_4_8.png|right|frame|Signalraumkonstellationen mit $M = 3$ Symbolen]] | + | [[File:P_ID2018__Dig_A_4_8.png|right|frame|Signalraumkonstellationen mit $M = 3$ Symbolen]] |
| − | Wir betrachten eine Signalraumkonstellation im zweidimensionalen Raum $(N = 2)$ mit der Signalmenge: | + | Wir betrachten eine Signalraumkonstellation im zweidimensionalen Raum $(N = 2)$ mit der Signalmenge: |
:$$\boldsymbol{ s }_0 = (-1, 1)\hspace{0.05cm}, \hspace{0.2cm} | :$$\boldsymbol{ s }_0 = (-1, 1)\hspace{0.05cm}, \hspace{0.2cm} | ||
\boldsymbol{ s }_1 = (1, 2)\hspace{0.05cm}, \hspace{0.2cm} | \boldsymbol{ s }_1 = (1, 2)\hspace{0.05cm}, \hspace{0.2cm} | ||
\boldsymbol{ s }_2 = (2, -1)\hspace{0.05cm},$$ | \boldsymbol{ s }_2 = (2, -1)\hspace{0.05cm},$$ | ||
| − | jeweils bezogen auf den Normierungswert $\sqrt {E}$. | + | jeweils bezogen auf den Normierungswert $\sqrt {E}$. |
| − | Gesucht sind die Entscheidungsregionen $I_0$, $I_1$ und $I_2$, wobei folgende Gesichtspunkte zu beachten sind: | + | Gesucht sind die Entscheidungsregionen $I_0$, $I_1$ und $I_2$, wobei folgende Gesichtspunkte zu beachten sind: |
| − | * Die Region $I_i$ soll den Signalraumpunkt $\boldsymbol{s}_i$ beinhalten ($i = 0, 1, 2$). | + | * Die Region $I_i$ soll den Signalraumpunkt $\boldsymbol{s}_i$ beinhalten ($i = 0, 1, 2$). |
| − | * Die Signale $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ sind gleichwahrscheinlich. | + | * Die Signale $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ sind gleichwahrscheinlich. |
| − | * Die Regionen | + | * Die Regionen sind so zu bestimmen, dass sich für den AWGN–Kanal die kleinste Fehlerwahrscheinlichkeit ergibt. |
| − | Mit diesen Voraussetzungen sind die Entscheidergrenzen $G_{\it ik}$ zwischen den Regionen $I_i$ und $I_k$ jeweils Geraden, die genau in der Mitte zwischen $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$ verlaufen ( | + | Mit diesen Voraussetzungen sind die Entscheidergrenzen $G_{\it ik}$ zwischen den Regionen $I_i$ und $I_k$ jeweils Geraden, die genau in der Mitte zwischen $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$ verlaufen $(i = 0, 1, 2; \ \ k = 0, 1, 2; \ \ i ≠ k)$. |
Mit Kreuzen sind in obiger Grafik drei Empfangswerte | Mit Kreuzen sind in obiger Grafik drei Empfangswerte | ||
| Line 23: | Line 23: | ||
\boldsymbol{ C } = (0.75, \hspace{0.1cm}0.50)$$ | \boldsymbol{ C } = (0.75, \hspace{0.1cm}0.50)$$ | ||
| − | eingezeichnet, die in der Teilaufgabe (5) jeweils einer Region $I_i$ zugeordnet werden sollen. | + | eingezeichnet, die in der Teilaufgabe '''(5)''' jeweils einer Region $I_i$ zugeordnet werden sollen. |
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| Approximation der Fehlerwahrscheinlichkeit]]. | + | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| Approximation der Fehlerwahrscheinlichkeit]]. |
* Zur Vereinfachung der Schreibweise wird nachfolgend verwendet: | * Zur Vereinfachung der Schreibweise wird nachfolgend verwendet: | ||
| Line 38: | Line 41: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lautet die Gleichung der Entscheidergrenze $G_{\rm 01}$? | + | {Wie lautet die Gleichung der Entscheidergrenze $G_{\rm 01}$? |
|type="[]"} | |type="[]"} | ||
| − | + $y = 3/2 \, | + | + $y = 3/2 \, -2 \cdot x$, |
- $y = x/3$, | - $y = x/3$, | ||
| − | - $y = \, | + | - $y = \, -3/4 + 3/2 \cdot x$. |
| − | {Wie lautet die Gleichung der Entscheidergrenze $G_{\rm 02}$? | + | {Wie lautet die Gleichung der Entscheidergrenze $G_{\rm 02}$? |
| − | |type=" | + | |type="()"} |
| − | - $y = 3/2 \, | + | - $y = 3/2 \, -2 \cdot x$, |
- $y = x/3$, | - $y = x/3$, | ||
| − | + $y = \, | + | + $y = \, -3/4 + 3/2 \cdot x$. |
| − | {Wie lautet die Gleichung der Entscheidergrenze $G_{\rm 12}$? | + | {Wie lautet die Gleichung der Entscheidergrenze $G_{\rm 12}$? |
| − | |type=" | + | |type="()"} |
| − | - $y = 3/2 \, | + | - $y = 3/2 \, -2 \cdot x$, |
+ $y = x/3$, | + $y = x/3$, | ||
| − | - $y = \, | + | - $y = \, -3/4 + 3/2 \cdot x$. |
| − | {Skizzieren Sie die drei Entscheidungsregionen $I_0$, $I_1$ und $I_2$. Schneiden sich die Entscheidungsgrenzen $G_{\rm 01}$, $G_{\rm 02}$ und $G_{\rm 12}$ in einem Punkt? | + | {Skizzieren Sie die drei Entscheidungsregionen $I_0$, $I_1$ und $I_2$. Schneiden sich die Entscheidungsgrenzen $G_{\rm 01}$, $G_{\rm 02}$ und $G_{\rm 12}$ in einem Punkt? |
|type="()"} | |type="()"} | ||
+ Ja. | + Ja. | ||
| Line 62: | Line 65: | ||
{Welche der folgenden Entscheidungen sind richtig? | {Welche der folgenden Entscheidungen sind richtig? | ||
| − | |type=" | + | |type="()"} |
| − | + $\boldsymbol{A} = (0.5, 0.25)$ gehört zur Region $I_0$. | + | + $\boldsymbol{A} = (0.5, 0.25)$ gehört zur Region $I_0$. |
| − | + $\boldsymbol{B} = (1, 0)$ gehört zur Region $I_2$. | + | + $\boldsymbol{B} = (1, 0)$ gehört zur Region $I_2$. |
| − | + $\boldsymbol{C} = (0.75, 0.5)$ gehört zur Region $I_1$. | + | + $\boldsymbol{C} = (0.75, 0.5)$ gehört zur Region $I_1$. |
</quiz> | </quiz> | ||
Revision as of 17:18, 13 March 2019
Wir betrachten eine Signalraumkonstellation im zweidimensionalen Raum $(N = 2)$ mit der Signalmenge:
- $$\boldsymbol{ s }_0 = (-1, 1)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_1 = (1, 2)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_2 = (2, -1)\hspace{0.05cm},$$
jeweils bezogen auf den Normierungswert $\sqrt {E}$.
Gesucht sind die Entscheidungsregionen $I_0$, $I_1$ und $I_2$, wobei folgende Gesichtspunkte zu beachten sind:
- Die Region $I_i$ soll den Signalraumpunkt $\boldsymbol{s}_i$ beinhalten ($i = 0, 1, 2$).
- Die Signale $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ sind gleichwahrscheinlich.
- Die Regionen sind so zu bestimmen, dass sich für den AWGN–Kanal die kleinste Fehlerwahrscheinlichkeit ergibt.
Mit diesen Voraussetzungen sind die Entscheidergrenzen $G_{\it ik}$ zwischen den Regionen $I_i$ und $I_k$ jeweils Geraden, die genau in der Mitte zwischen $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$ verlaufen $(i = 0, 1, 2; \ \ k = 0, 1, 2; \ \ i ≠ k)$.
Mit Kreuzen sind in obiger Grafik drei Empfangswerte
- $$\boldsymbol{ A } = (0.50, \hspace{0.1cm}0.25)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ B } = (1, \hspace{0.1cm}0)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ C } = (0.75, \hspace{0.1cm}0.50)$$
eingezeichnet, die in der Teilaufgabe (5) jeweils einer Region $I_i$ zugeordnet werden sollen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Approximation der Fehlerwahrscheinlichkeit.
- Zur Vereinfachung der Schreibweise wird nachfolgend verwendet:
- $$x = {\varphi_1(t)}/{\sqrt{E}}\hspace{0.05cm}, \hspace{0.2cm} y = {\varphi_2(t)}/{\sqrt{E}}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
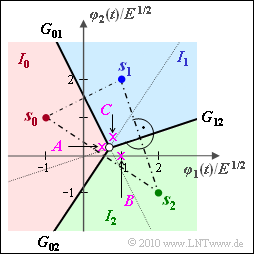
(1) Richtig ist der Lösungsvorschlag 1:
- Die Verbindungslinie zwischen den Signalpunkten $\boldsymbol{s}_0 = (–1, 1)$ und $\boldsymbol{s}_1 = (1, 2)$ hat die Steigung $1/2$ (siehe Grafik).
- Die Entscheidungsgrenze schneidet die Verbindungslinie bei $(\boldsymbol{s}_0 + \boldsymbol{s}_1)/2 = (0, 1.5)$ und weist die Steigung $2$ auf (Drehung der Verbindungslinie um 90°).
- Daraus folgt: $y = 1.5 - 2 x \hspace{0.05cm}.$
(2) Richtig ist der Lösungsvorschlag 3:
- Die Verbindungslinie zwischen $\boldsymbol{s}_0 = (–1, 1)$ und $\boldsymbol{s}_2 = (2, 1)$ besitzt die Steigung $–2/3$ und schneidet die Entscheidergrenze $G_{\rm 02}$ (mit der Steigung $3/2$) bei $(0.5, 0)$.
- Daraus folgt: $y = {3}/{2} \left ( x - {1}/{2} \right ) = -{3}/{4} + {3}/{2} \cdot x\hspace{0.05cm}.$
(3) Hier ist der Lösungsvorschlag 2 zutreffend:
- Die Verbindungslinie zwischen $\boldsymbol{s}_1 = (1, 2)$ und $\boldsymbol{s}_2 = (2, \, –1)$ schneidet die Entscheidungsgrenze $G_{\rm 12}$ bei $(1.5, 0.5)$ und besitzt die Steigung $–3$.
- Demzufolge ist die Steigung von $G_{\rm 12} = 1/3$ und die Gleichung der Entscheidungsgrenze $G_{\rm 12}$ lautet:
- $$y - {1}/{2} = {1}/{3} \cdot \left ( x - {3}/{2} \right ) = {x}/{3} - {1}/{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y = {x}/{3} \hspace{0.05cm}.$$
(4) Die Grafik zeigt bereits, dass die Antwort JA ist. Der Schnittpunkt von $G_{\rm 01}$ und $G_{\rm 12}$ (weißer Kreis) liegt bei $(9/14, 3/14)$, wegen
- $${3}/{2} - 2 x = {x}/{3} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {3}/{2} = {7}/{3} \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y = {3}/{14} \hspace{0.05cm}.$$
Auch die Gerade $G_{\rm 02}$ geht durch diesen Punkt:
- $$y(x = {9}/{14}) =-{3}/{4} + {3}/{2} \cdot x = -{3}/{4} + {3}/{2} \cdot {9}/{14} =\frac{-21+27}{28}= {3}/{14} \hspace{0.05cm}.$$
(5) Gemäß der Grafik sind alle genannten Aussagen richtig.