Difference between revisions of "Aufgaben:Exercise 5.6Z: Gilbert-Elliott Model"
| Line 73: | Line 73: | ||
| − | '''(2)''' Das GE–Modell ist eine stationäre Markovkette. Für die Wahrscheinlichkeit, dass sich diese im Zustand „GOOD” befindet, gilt unter Berücksichtigung des Ergebnisses der Teilaufgabe (1): | + | '''(2)''' Das GE–Modell ist eine stationäre Markovkette. |
| + | *Für die Wahrscheinlichkeit, dass sich diese im Zustand „GOOD” befindet, gilt unter Berücksichtigung des Ergebnisses der Teilaufgabe '''(1)''': | ||
:$$w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) \cdot | :$$w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) \cdot | ||
w_{\rm G} + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot | w_{\rm G} + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot | ||
| Line 82: | Line 83: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Weiter gilt $w_{\rm B} = 1 \, –w_{\rm G}$: | + | *Weiter gilt $w_{\rm B} = 1 \, –w_{\rm G}$: |
:$${\rm Pr}(\rm | :$${\rm Pr}(\rm | ||
B\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} + {\rm Pr}(\rm | B\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} + {\rm Pr}(\rm | ||
| Line 93: | Line 94: | ||
\hspace{0.15cm}\underline {\approx 0.909} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - | \hspace{0.15cm}\underline {\approx 0.909} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - | ||
w_{\rm G }\hspace{0.15cm}\underline {\approx 0.091}\hspace{0.05cm}.$$ | w_{\rm G }\hspace{0.15cm}\underline {\approx 0.091}\hspace{0.05cm}.$$ | ||
| + | |||
| Line 98: | Line 100: | ||
:$$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} | :$$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} | ||
= \frac{10}{11} \cdot 10^{-3} + \frac{1}{11} \cdot 10^{-1}= \frac{10+100}{11} \cdot 10^{-3}\hspace{0.15cm}\underline { = | = \frac{10}{11} \cdot 10^{-3} + \frac{1}{11} \cdot 10^{-1}= \frac{10+100}{11} \cdot 10^{-3}\hspace{0.15cm}\underline { = | ||
| − | + | 1\%}\hspace{0.05cm}.$$ | |
| Line 127: | Line 129: | ||
p_{\rm M} \hspace{0.05cm}.$$ | p_{\rm M} \hspace{0.05cm}.$$ | ||
| − | Mit dem Ergebnis der Teilaufgabe (3) ergibt sich für den vorliegenden Fall $\varphi_e(k = 0) \ \underline {= 0.01}$. | + | Mit dem Ergebnis der Teilaufgabe '''(3)''' ergibt sich für den vorliegenden Fall $\varphi_e(k = 0) \ \underline {= 0.01}$. |
| + | |||
| − | '''(6)''' Entsprechend der Teilaufgabe (3) gilt | + | '''(6)''' Entsprechend der Teilaufgabe '''(3)''' gilt: |
:$$p_{\rm M} = {10}/{11} \cdot p_{\rm G} + {1}/{11} \cdot | :$$p_{\rm M} = {10}/{11} \cdot p_{\rm G} + {1}/{11} \cdot | ||
p_{\rm B} \hspace{0.05cm}.$$ | p_{\rm B} \hspace{0.05cm}.$$ | ||
| − | Bei vorgegebenem $p_{\rm B} = 0.1$ ergibt sich selbst für $p_{\rm G} = 0$ (kein Fehler im Zustand „G”) die mittlere Fehlerwahrscheinlichkeit zu $p_{\rm M} \approx 0.009$. Dagegen ist mit festem $p_{\rm G} = 0.001$ der Wert $p_{\rm M} = 0.005$ | + | *Bei vorgegebenem $p_{\rm B} = 0.1$ ergibt sich selbst für $p_{\rm G} = 0$ (kein Fehler im Zustand „G”) die mittlere Fehlerwahrscheinlichkeit zu $p_{\rm M} \approx 0.009$. |
| − | erreichbar: | + | *Dagegen ist mit festem $p_{\rm G} = 0.001$ der Wert $p_{\rm M} = 0.005$ erreichbar: |
:$$0.005 = {10}/{11} \cdot 10^{-3} + {1}/{11} \cdot p_{\rm B} | :$$0.005 = {10}/{11} \cdot 10^{-3} + {1}/{11} \cdot p_{\rm B} | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} \le 0.055 - 0.1 | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} \le 0.055 - 0.1 | ||
= 4.5\%\hspace{0.05cm}.$$ | = 4.5\%\hspace{0.05cm}.$$ | ||
| − | Weiterhin kann die mittlere Fehlerwahrscheinlichkeit (mit vorgegebenem $p_{\rm G}$ und $p_{\rm B}$) auch wie folgt dargestellt werden: | + | *Weiterhin kann die mittlere Fehlerwahrscheinlichkeit (mit vorgegebenem $p_{\rm G}$ und $p_{\rm B}$) auch wie folgt dargestellt werden: |
:$$p_{\rm M} = \frac{p_{\rm G} \cdot {\rm Pr}(\rm | :$$p_{\rm M} = \frac{p_{\rm G} \cdot {\rm Pr}(\rm | ||
G\hspace{0.05cm}|\hspace{0.05cm} B)+ p_{\rm B} \cdot {\rm Pr}(\rm | G\hspace{0.05cm}|\hspace{0.05cm} B)+ p_{\rm B} \cdot {\rm Pr}(\rm | ||
| Line 151: | Line 154: | ||
B\hspace{0.05cm}|\hspace{0.05cm} G)}\hspace{0.05cm}.$$ | B\hspace{0.05cm}|\hspace{0.05cm} G)}\hspace{0.05cm}.$$ | ||
| − | Mit $\rm Pr(B|G) = 0.01$ bzw. mit $\rm Pr(G|B) = 0.1$ erhält man folgende Gleichungen: | + | *Mit $\rm Pr(B|G) = 0.01$ bzw. mit $\rm Pr(G|B) = 0.1$ erhält man folgende Gleichungen: |
:$${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = | :$${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = | ||
0.01\hspace{-0.15cm}:\hspace{0.2cm} {\it p}_{\rm M} \hspace{-0.1cm} \ = \ | 0.01\hspace{-0.15cm}:\hspace{0.2cm} {\it p}_{\rm M} \hspace{-0.1cm} \ = \ | ||
| Line 164: | Line 167: | ||
G\hspace{0.05cm}|\hspace{0.05cm} B) }\hspace{0.05cm}.$$ | G\hspace{0.05cm}|\hspace{0.05cm} B) }\hspace{0.05cm}.$$ | ||
| − | Aus der | + | *Aus der letzten Gleichung ist zu erkennen, dass mit keinem $\rm Pr(G|B)$–Wert das Ergebnis $p_{\rm M} = 0.005$ möglich ist. |
| + | *Dagegen lässt sich durch ein kleineres $\rm Pr(B|G)$ die Bedingung erfüllen: | ||
:$$0.005 = \frac{0.0001 + 0.1 \cdot {\rm Pr}(\rm | :$$0.005 = \frac{0.0001 + 0.1 \cdot {\rm Pr}(\rm | ||
B\hspace{0.05cm}|\hspace{0.05cm} G)}{0.1 +{\rm Pr}(\rm | B\hspace{0.05cm}|\hspace{0.05cm} G)}{0.1 +{\rm Pr}(\rm | ||
| Line 171: | Line 175: | ||
\frac{0.0004}{0.095} \approx 0.0042\hspace{0.05cm}.$$ | \frac{0.0004}{0.095} \approx 0.0042\hspace{0.05cm}.$$ | ||
| − | Richtig sind somit die <u>Lösungsvorschläge 2 und 4</u>. | + | *Richtig sind somit die <u>Lösungsvorschläge 2 und 4</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Aufgaben zu Digitalsignalübertragung|^5.3 Bündelfehlerkanäle^]] | [[Category:Aufgaben zu Digitalsignalübertragung|^5.3 Bündelfehlerkanäle^]] | ||
Revision as of 14:48, 26 March 2019
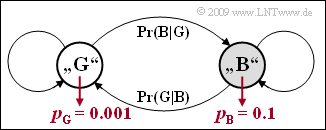
Wir betrachten das Bündelfehler–Kanalmodell nach E.N. Gilbert und E.O. Elliott (siehe Skizze). Für die Übergangswahrscheinlichkeiten soll dabei gelten:
- $${\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)= 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
Die Fehlerwahrscheinlichkeit im Zustand „GOOD” betrage $p_{\rm G} = 0.1\%$. Für den Zustand „BAD” gelte $p_{\rm B} = 10\%$.
Im Verlaufe dieser Aufgabe sollen weitere Kenngrößen ermittelt werden:
- die mittlere Fehlerwahrscheinlichkeit $p_{\rm M}$,
- die Zustandswahrscheinlichkeiten $w_{\rm G} = \rm Pr(Z = G)$ und $w_{\rm B} = \rm Pr(Z = B)$,
- die Werte der Korrelationsfunktion, die für $k > 0$ analytisch wie folgt gegeben ist:
- $$\varphi_{e}(k) = p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot \big [1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )\big ]^{\it k} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Bündelfehlerkanäle.
- Bezug genommen wird aber auch auf das Kapitel Markovketten im Buch „Stochastische Signaltheorie” und insbesondere auf die Seite Fehlerkorrelationsfunktion des GE–Modells im Buch „Kanalcodierung”.
Fragebogen
Musterlösung
(2) Das GE–Modell ist eine stationäre Markovkette.
- Für die Wahrscheinlichkeit, dass sich diese im Zustand „GOOD” befindet, gilt unter Berücksichtigung des Ergebnisses der Teilaufgabe (1):
- $$w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot w_{\rm B}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot w_{\rm B} \hspace{0.05cm}.$$
- Weiter gilt $w_{\rm B} = 1 \, –w_{\rm G}$:
- $${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)$$
- $$\Rightarrow \hspace{0.3cm} w_{\rm G} = \frac{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.1}{0.1 + 0.01} \hspace{0.15cm}\underline {\approx 0.909} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - w_{\rm G }\hspace{0.15cm}\underline {\approx 0.091}\hspace{0.05cm}.$$
(3) Die mittlere Fehlerwahrscheinlichkeit $p_{\rm M}$ ergibt sich aus den Fehlerwahrscheinlichkeiten $p_{\rm G}$ und $p_{\rm B}$, gewichtet mit $w_{\rm G}$ und $w_{\rm B}$:
- $$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \frac{10}{11} \cdot 10^{-3} + \frac{1}{11} \cdot 10^{-1}= \frac{10+100}{11} \cdot 10^{-3}\hspace{0.15cm}\underline { = 1\%}\hspace{0.05cm}.$$
(4) Entsprechend der allgemeinen Gleichung auf dem Angabenblatt gilt für $k > 0$:
- $$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot [1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]^{\it k} = 10^{-4} + 0.09 \cdot 0.009 \cdot 0.89^{\it k} = 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{\it k} \right )\hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 1 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 1} \right ) \hspace{0.15cm}\underline {= 8.209 \cdot 10^{-4}} \hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 2 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 2} \right )\hspace{0.15cm}\underline { = 7.416 \cdot 10^{-4}} \hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 5 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 5} \right )\hspace{0.15cm}\underline {= 5.523 \cdot 10^{-4}} \hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 50 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 50} \right ) \hspace{0.15cm}\underline {= 1.024 \cdot 10^{-4}} \hspace{0.05cm}.$$
(5) Für jedes Kanalmodell gilt wegen $e_{\nu} ∈ \{0, 1\}$:
- $$\varphi_{e}(k = 0 ) = {\rm E}[e_{\nu} ^2] = {\rm E}[e_{\nu} ] = p_{\rm M} \hspace{0.05cm}.$$
Mit dem Ergebnis der Teilaufgabe (3) ergibt sich für den vorliegenden Fall $\varphi_e(k = 0) \ \underline {= 0.01}$.
(6) Entsprechend der Teilaufgabe (3) gilt:
- $$p_{\rm M} = {10}/{11} \cdot p_{\rm G} + {1}/{11} \cdot p_{\rm B} \hspace{0.05cm}.$$
- Bei vorgegebenem $p_{\rm B} = 0.1$ ergibt sich selbst für $p_{\rm G} = 0$ (kein Fehler im Zustand „G”) die mittlere Fehlerwahrscheinlichkeit zu $p_{\rm M} \approx 0.009$.
- Dagegen ist mit festem $p_{\rm G} = 0.001$ der Wert $p_{\rm M} = 0.005$ erreichbar:
- $$0.005 = {10}/{11} \cdot 10^{-3} + {1}/{11} \cdot p_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} \le 0.055 - 0.1 = 4.5\%\hspace{0.05cm}.$$
- Weiterhin kann die mittlere Fehlerwahrscheinlichkeit (mit vorgegebenem $p_{\rm G}$ und $p_{\rm B}$) auch wie folgt dargestellt werden:
- $$p_{\rm M} = \frac{p_{\rm G} \cdot {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)+ p_{\rm B} \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.001 \cdot {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)+ 0.1 \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}\hspace{0.05cm}.$$
- Mit $\rm Pr(B|G) = 0.01$ bzw. mit $\rm Pr(G|B) = 0.1$ erhält man folgende Gleichungen:
- $${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{-0.15cm}:\hspace{0.2cm} {\it p}_{\rm M} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{0.001 \cdot {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)+ 0.001 }{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + 0.01}\hspace{0.05cm},\hspace{0.5cm} {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) = 0.1\hspace{-0.15cm}:\hspace{0.2cm}{\it p}_{\rm M} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{0.0001 + 0.1 \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{0.1 +{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) }\hspace{0.05cm}.$$
- Aus der letzten Gleichung ist zu erkennen, dass mit keinem $\rm Pr(G|B)$–Wert das Ergebnis $p_{\rm M} = 0.005$ möglich ist.
- Dagegen lässt sich durch ein kleineres $\rm Pr(B|G)$ die Bedingung erfüllen:
- $$0.005 = \frac{0.0001 + 0.1 \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{0.1 +{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) } \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) \le \frac{0.0004}{0.095} \approx 0.0042\hspace{0.05cm}.$$
- Richtig sind somit die Lösungsvorschläge 2 und 4.