|
|
| Line 10: |
Line 10: |
| | ==Theoretischer Hintergrund== | | ==Theoretischer Hintergrund== |
| | <br> | | <br> |
| − | Bei der Untersuchung digitaler Übertragungssysteme muss oft die Wahrscheinlichkeit bestimmt werden, dass eine (mittelwertfreie) gaußverteilte Zufallsgröße $x$ mit der Varianz $σ^2$ einen vorgegebenen Wert $x_0$ überschreitet. Für diese Wahrscheinlichkeit gilt:
| |
| − | :$${\rm Pr}(x > x_0)={\rm Q}(\frac{x_0}{\sigma}) = 1/2 \cdot {\rm erfc}(\frac{x_0}{\sqrt{2} \cdot \sigma}).$$
| |
| − | <br>
| |
| − |
| |
| − | ===Die Funktion ${\rm Q}(x )$===
| |
| − | <br>
| |
| − | Die Funktion ${\rm Q}(x)$ bezeichnet man als das ''Komplementäre Gaußsche Fehlerintegral''. Es gilt folgende Berechnungsvorschrift:
| |
| − | :$${\rm Q}(x ) = \frac{1}{\sqrt{2\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}/\hspace{0.05cm} 2}\,{\rm d} u .$$
| |
| − | *Dieses Integral ist nicht analytisch lösbar und muss – wenn man dieses Applet nicht zur Verfügung hat – aus Tabellen entnommen werden.
| |
| − | *Speziell für größere $x$–Werte (also für kleine Fehlerwahrscheinlichkeiten) liefern die nachfolgend angegebenen Schranken eine brauchbare Abschätzung für das Komplementäre Gaußsche Fehlerintegral, die auch ohne Tabellen berechnet werden können.
| |
| − | *Eine obere Schranke (englisch: ''Upper Bound '') des Komplementären Gaußschen Fehlerintegrals lautet:
| |
| − | :$${\rm Q}_{\rm UB}(x )=\text{Upper Bound }\big [{\rm Q}(x ) \big ] = \frac{ 1}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{- x^{2}/\hspace{0.05cm}2} > {\rm Q}(x).$$
| |
| − | *Entsprechend gilt für die untere Schranke (englisch: ''Lower Bound ''):
| |
| − | :$${\rm Q}_{\rm LB}(x )=\text{Lower Bound }\big [{\rm Q}(x ) \big ] =\frac{1-1/x^2}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{-x^ 2/\hspace{0.05cm}2} ={\rm Q}_{\rm UB}(x ) \cdot (1-1/x^2)< {\rm Q}(x).$$
| |
| − |
| |
| − | In vielen Programmbibliotheken findet man allerdings die Funktion ${\rm Q}(x )$ nicht.
| |
| − | <br>
| |
| − |
| |
| | | | |
| − | ===Die Funktion $1/2 \cdot {\rm erfc}(x )$===
| + | Die Walsh-Funktionen sind eine Gruppe von periodischen orthogonalen Funktionen. Ihr Anwendungsbereich in der digitalen Signalverarbeitung liegt vor allem in der Verwendung zur Bandspreizung bei CDMA-Systemen, beispielsweise dem Mobilfunkstandard UMTS. Aufgrund ihrer Orthogonalitätseigenschaften und der günstigen PKKF-Bedingungen stellen die Walsh-Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA-System optimale Spreizfolgen dar. |
| − | <br>
| |
| − | In fast allen Programmbibliotheken findet man dagegen die ''Komplementäre Gaußsche Fehlerfunktion'' (englisch: ''Complementary Gaussian Error Function'')
| |
| − | :$${\rm erfc}(x) = \frac{2}{\sqrt{\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}}\,{\rm d} u .$$
| |
| − | die mit ${\rm Q}(x)$ wie folgt zusammenhängt: ${\rm Q}(x)=1/2\cdot {\rm erfc}(x/{\sqrt{2}}).$ Da bei fast allen Anwendungen diese Funktion mit dem Faktor $1/2$ verwendet wird, wurde in diesem Applet genau diese Funktion realisiert: | |
| − | :$$1/2 \cdot{\rm erfc}(x) = \frac{1}{\sqrt{\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}}\,{\rm d} u .$$
| |
| | | | |
| − | *Auch für diese Funktion kann wieder eine obere und eine untere Schranke angegeben werden:
| |
| − | :$$\text{Upper Bound }\big [1/2 \cdot{\rm erfc}(x) \big ] = \frac{ 1}{\sqrt{\pi}\cdot 2x}\cdot {\rm e}^{- x^{2}} ,$$
| |
| − | :$$\text{Lower Bound }\big [1/2 \cdot{\rm erfc}(x) \big ] = \frac{ {1-1/(2x^2)}}{\sqrt{\pi}\cdot 2x}\cdot {\rm e}^{- x^{2}} .$$
| |
| | <br> | | <br> |
| | | | |
| − | ===Wann bietet welche Funktion Vorteile?===
| + | Die Konstruktion der Walsh-Funktionen kann rekursiv mithilfe der Hadamard-Matrizen erfolgen. Eine Hadamard-Matrix $H_J$ der Ordnung $J$ ist eine $J\times J$-Matrix, die zeilenweise die $\pm 1$-Gewichte der Walsh-Folgen enthält. Die Ordnungen der Hadamard-Matrizen sind dabei auf Zweierpotenzen festgelegt, d.h. es gilt $J = 2^G$ für eine natürliche Zahl $G$. Ausgehend von $H_1 = (+1)$ und |
| − | <br>
| |
| − | {{GraueBox|TEXT=
| |
| − | $\text{Beispiel 1:}$ Wir betrachten die binäre Basisbandübertragung. Hier lautet die Bitfehlerwahrscheinlichkeit $p_{\rm B} = {\rm Q}({s_0}/{\sigma_d})$, wobei das Nutzsignal die Werte $\pm s_0$ annehmen kann und der Rauscheffektivwert $\sigma_d$ ist. | |
| | | | |
| − | Es wird vorausgesetzt, dass Tabellen zur Verfügung stehen, in denen das Argument der Gaußschen Fehlerfunktionen im Abstand $0.1$ aufgelistet sind. Mit $s_0/\sigma_d = 4$ erhält man für die Bitfehlerwahrscheinlichkeit gemäß der Q–Funktion:
| + | \begin{equation} |
| − | :$$p_{\rm B} = {\rm Q} (4) \approx 0.317 \cdot 10^{-4}\hspace{0.05cm}.$$
| + | H_2 = |
| − | Nach der zweiten Gleichung ergibt sich:
| + | \left( \begin{array}{rr} |
| − | :$$p_{\rm B} = {1}/{2} \cdot {\rm erfc} ( {4}/{\sqrt{2} })= {1}/{2} \cdot {\rm erfc} ( 2.828)\approx {1}/{2} \cdot {\rm erfc} ( 2.8)= 0.375 \cdot 10^{-4}\hspace{0.05cm}.$$
| + | +1 & +1\\ |
| − | *Richtiger ist der erste Wert. Bei der zweiten Berechnungsart muss man runden oder – noch besser – interpolieren, was aufgrund der starken Nichtlinearität dieser Funktion sehr schwierig ist.<br>
| + | +1 & -1 \\ |
| − | *Bei den gegebenen Zahlenwerten ist demnach Q–Funktion besser geeignet. Außerhalb von Übungsbeispielen wird allerdings $s_0/\sigma_d$ in der Regel einen „krummen” Wert besitzen. In diesem Fall bietet ${\rm Q}(x)$ natürlich keinen Vorteil gegenüber $1/2 \cdot{\rm erfc}(x)$. }}
| + | \end{array}\right) |
| − | | + | \end{equation} |
| − | | + | gilt der folgende Zusammenhang zur Generierung weiterer Hadamard-Matrizen: |
| − | {{GraueBox|TEXT=
| + | \begin{equation} |
| − | $\text{Beispiel 2:}$
| + | H_{2N} = |
| − | Mit der Energie pro Bit $(E_{\rm B})$ und der Rauschleistungsdichte $(N_0)$ gilt für die Bitfehlerwahrscheinlichkeit von ''Binary Phase Shift Keying'' (BPSK):
| + | \left( \begin{array}{rr} |
| − | :$$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2 E_{\rm B} }/{N_0} }\right ) = {1}/{2} \cdot {\rm erfc} \left ( \sqrt{ {E_{\rm B} }/{N_0} }\right ) \hspace{0.05cm}.$$
| + | +H_N & +H_N\\ |
| − | Für die Zahlenwerte $E_{\rm B} = 16 \ \rm mWs$ und $N_0 = 16 \ \rm mW/Hz$ erhält man:
| + | +H_N & -H_N \\ |
| − | :$$p_{\rm B} = {\rm Q} \left (4 \cdot \sqrt{ 2} \right ) = {1}/{2} \cdot {\rm erfc} \left ( 4\right ) \hspace{0.05cm}.$$
| + | \end{array}\right) |
| − | *Der erste Weg führt zum Ergebnis $p_{\rm B} = {\rm Q} (5.657) \approx {\rm Q} (5.7) = 0.6 \cdot 10^{-8}\hspace{0.05cm}$, während $1/2 \cdot{\rm erfc}(x)$ hier den richtigeren Wert $p_{\rm B} \approx 0.771 \cdot 10^{-8}$ liefert.
| + | \end{equation} |
| − | *Wie im ersten Beispiel erkennt man aber auch hier: Die Funktionen ${\rm Q}(x)$ und $1/2 \cdot{\rm erfc}(x)$ sind grundsätzlich gleich gut geeignet. Vor– oder Nachteile der einen oder anderen Funktion ergeben sich nur bei konkreten Zahlenwerten.}}
| |
| | <br> | | <br> |
| − |
| |
| | | | |
| | ==Zur Handhabung des Applets== | | ==Zur Handhabung des Applets== |
Open Applet in a new tab
Programmbeschreibung
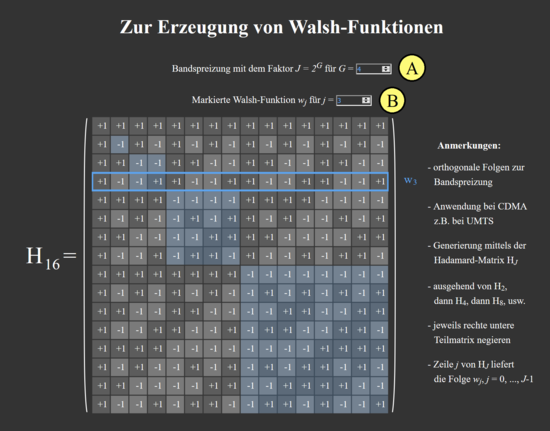
Dieses Applet ermöglicht die Darstellung der Hadamard-Matrizen $H_J$ zur Konstruktion der Walsh-Funktionen $w_j$. Dabei können der Faktor $J$ der Bandspreizung sowie die Markierung der einzelnen Walsh-Funktionen (durch blaue Umrandung der Zeilen der Matrix) verändert werden.
Theoretischer Hintergrund
Die Walsh-Funktionen sind eine Gruppe von periodischen orthogonalen Funktionen. Ihr Anwendungsbereich in der digitalen Signalverarbeitung liegt vor allem in der Verwendung zur Bandspreizung bei CDMA-Systemen, beispielsweise dem Mobilfunkstandard UMTS. Aufgrund ihrer Orthogonalitätseigenschaften und der günstigen PKKF-Bedingungen stellen die Walsh-Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA-System optimale Spreizfolgen dar.
Die Konstruktion der Walsh-Funktionen kann rekursiv mithilfe der Hadamard-Matrizen erfolgen. Eine Hadamard-Matrix $H_J$ der Ordnung $J$ ist eine $J\times J$-Matrix, die zeilenweise die $\pm 1$-Gewichte der Walsh-Folgen enthält. Die Ordnungen der Hadamard-Matrizen sind dabei auf Zweierpotenzen festgelegt, d.h. es gilt $J = 2^G$ für eine natürliche Zahl $G$. Ausgehend von $H_1 = (+1)$ und
\begin{equation}
H_2 =
\left( \begin{array}{rr}
+1 & +1\\
+1 & -1 \\
\end{array}\right)
\end{equation}
gilt der folgende Zusammenhang zur Generierung weiterer Hadamard-Matrizen:
\begin{equation}
H_{2N} =
\left( \begin{array}{rr}
+H_N & +H_N\\
+H_N & -H_N \\
\end{array}\right)
\end{equation}
Zur Handhabung des Applets
(A) Auswahl des Faktors zur Bandspreizung als Zweierpotenz von $G$
(B) Auswahl der jeweiligen Walsh-Funktion $w_j$
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2007 von Thomas Großer im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018/2019 wurde das Programm von Marwen Ben Ammar und Xiaohan Liu (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.
Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
Open Applet in a new tab