Aufgaben:Exercise 1.13: Binary Erasure Channel Decoding

• Return to book

Zur Decodierung beim BEC

Wir gehen hier vom Modell im Abschnitt  Decodierung beim Binary Erasure Channel  aus (grün hinterlegte BEC–Konfiguration):

• Jedes Informationswort  $\underline{u}$  wird blockweise codiert und liefert das Codewort  $\underline{x}$. Der Blockcode sei linear und durch seine Prüfmatrix  $\boldsymbol{\rm H}$ vollständig gegeben.

• Bei der Übertragung werden  $n_{\rm E}$  Bit des Codewortes ausgelöscht   ⇒  Binary Erasure Channel  (BEC). Aus dem Codewort  $\underline{x}$  wird somit das Empfangswort  $\underline{y}$.

• Ist die Anzahl  $n_{\rm E}$  der Auslöschungen kleiner als die  minimale Distanz  $d_{\rm min}$  des Codes, so gelingt es, aus  $\underline{y}$  das Codewort  $\underline{z} = \underline{x}$  ohne Fehler zu rekonstruieren, und man erhält so auch das richtige Informationswort  $\underline{v} = \underline{u}$.

Zur Aufgabenbeschreibung betrachten wir nun beispielhaft das Hamming–Codewort  $\underline{x} = (0, 1, 0, 1, 1, 0, 0)$  und das Empfangswort  $\underline{y} = (0, 1, {\rm E} , {\rm E}, 1, 0, 0).$

• Ausgelöscht wurden somit durch den Kanal das dritte und vierte Bit.
• Der Codewortfinder hat somit die Aufgabe, den Vektor  $z_{\rm E} = (z_{3}, z_{4})$ mit $z_{3}, \ z_{4} \in \{0, 1\}$  zu bestimmen. Dies geschieht entsprechend der Gleichung

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.05cm}.$$

• Im vorliegenden Beispiel gilt:

$$\underline{z}_{\rm K} = (0, 1, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &1 &0 &0\\ 0 &1 &0 &1 &0\\ 1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &1\\ 0 &1 \end{pmatrix} \hspace{0.05cm}.$$

• Diese Gleichung liefert zwei Bestimmungsgleichungen für die zu bestimmenden Bits, deren Lösung zum Ergebnis  $z_{3} = 0$  und  $z_{4} = 1$  führt.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Decodierung linearer Blockcodes.
• Der Algorithmus zur Zuordnung des Empfangswortes  $\underline{y}$  zum richtigen Codewort  $\underline{z} = \underline{x}$  ist im  Theorieteil  ausführlich beschrieben.
• Wir möchten nochmals daran erinnern, dass wir bei der BEC–Decodierung den ersten Decoderblock  $\underline{y} → \underline{z}$  als  Codewortfinder  bezeichnen, da hier Fehlentscheidungen ausgeschlossen sind. Jedes Empfangswort wird richtig decodiert, oder es kann gar nicht decodiert werden.
• Beim BSC–Modell lassen sich dagegen Decodierfehler nicht vermeiden. Dementsprechend bezeichnen wir den entsprechenden Block dort als  Codewortschätzer.

Fragebogen

1

Empfangen wurde  $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$. Für welche Sequenz entscheidet sich der Codewortfinder?

	$\underline{z} = (1, 0, 0, 1, 0, 0, 0),$
	$\underline{z} = (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} = (1, 0, 0, 1, 0, 0, 1).$

2

Welche Konsequenzen ergeben sich aus den roten Eintragungen für  $\boldsymbol{\rm H}_{\rm K}$  und  $z_{\rm K}$  (siehe Grafik auf der Angabenseite)?

	Der Erasure–Vektor lautet  $\underline{z}_{\rm E} = (z_{5}, z_{6}, z_{7}).$
	Das Empfangswort lautet  $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E}).$
	$\boldsymbol{\rm H}_{\rm E}$  ist eine  $2 \times 3$–Matrix.
	$\boldsymbol{\rm H}_{\rm E}$  ist eine  $3 \times 3$–Matrix.

3

Nun gelte  $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E}).$ Welches Codewort wird ausgewählt?

	$\underline{z} = (1, 1, 0, 1, 1, 1, 0),$
	$\underline{z} = (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} = (1, 1, 0, 0, 0, 1, 0).$
	Für das vorliegende  $\underline{y}$  ist keine eindeutige Decodierung möglich.

4

Welche Konsequenzen ergeben sich aus den grünen Eintragungen für  $\boldsymbol{\rm H}_{\rm K}$  und  $z_{\rm K}$  (siehe Grafik auf der Angabenseite)?

	Das Empfangswort lautet  $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E}).$
	$\boldsymbol{\rm H}_{\rm K}$  unterscheidet sich gegenüber Teilfrage (2) in der letzten Zeile.
	$\boldsymbol{\rm H}_{\rm K}$  unterscheidet sich gegenüber Teilfrage (2) in der letzten Spalte.

5

Nun gelte  $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E}).$ Welches Codewort wird ausgewählt?

	$\underline{z} = (1, 1, 0, 1, 1, 1, 0),$
	$\underline{z} = (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} = (1, 1, 0, 0, 0, 1, 0).$
	Für das vorliegende  $\underline{y}$  ist keine eindeutige Decodierung möglich.

6

Welche Aussagen ergeben sich für die Korrekturfähigkeit beim BEC? $n_{\rm E}$  gibt im Folgenden die Anzahl der Auslöschungen (Erasures) an.

	Für  $n_{\rm E} < d_{\rm min}$  ist stets eine eindeutige Decodierung möglich.
	Für  $n_{\rm E} = d_{\rm min}$  ist stets eine eindeutige Decodierung möglich.
	Für  $n_{\rm E} = d_{\rm min}$  ist manchmal eine eindeutige Decodierung möglich.
	Für  $n_{\rm E} > d_{\rm min}$  ist eine eindeutige Decodierung nie möglich.

Musterlösung

Solution

(1)  Der Empfangsvektor lautet $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$. Ausgelöscht wurden also die Codesymbole an den Positionen 2 und 7.

Ausgehend von der vorgegebenen Prüfmatrix

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix}$$

des Hammingcodes erhält man für Vektor und Matrix

• hinsichtlich aller korrekt übertragenen Codesymbole (Index $\rm K$), die dem Codewortfinder bekannt sind:

$$\underline{z}_{\rm K} = (1, 0, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &0 &1 &0\\ 0 &1 &1 &0 &1\\ 1 &0 &1 &0 &0 \end{pmatrix} \hspace{0.05cm},$$

• hinsichtlich der beiden ausgelöschten Codesymbole $z_{2}$ und $z_{7}$ (Index $\rm E$), die zu ermitteln sind:

$$\underline{z}_{\rm E} = (z_2, z_7)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &0\\ 1 &1 \end{pmatrix} \hspace{0.05cm}.$$

Die Bestimmungsgleichung lautet somit:

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} 1 &0\\ 1 &0\\ 1 &1 \end{pmatrix} \cdot \begin{pmatrix} z_2 \\ z_7 \end{pmatrix} = \begin{pmatrix} 1 &1 &0 &1 &0\\ 0 &1 &1 &0 &1\\ 1 &0 &1 &0 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \hspace{0.05cm}.$$

Daraus ergeben sich drei Gleichungen für die beiden Unbekannten $z_{2}$ und $z_{7}$:

$${\rm (a)}\ z_{2} = 1,$$

$${\rm (b)}\ z_{2} = 1,$$

$${\rm (c)}\ z_{2} + z_{7} = 0 \ \Rightarrow \ z_{7}= 1.$$

Somit liefert der Codewortfinder $\underline{z} = (1, 1, 0, 1, 0, 0, 1)$   ⇒   Lösungsvorschlag 2.

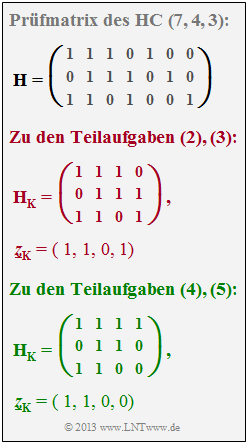
(2)  Betrachtet man die vorgegebene Matrix $\boldsymbol{\rm H}_{\rm K}$, so erkennt man, dass diese mit den ersten vier Spalten der Prüfmatrix $\boldsymbol{\rm H}$ übereinstimmt.

• Die Auslöschungen betreffen also die letzten drei Bit des Empfangswortes   ⇒   $\underline{z}_{\rm E} = (z_{5}, z_{6}, z_{7})   ⇒   \underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E})$.
• Die Erasure–Matrix lautet:

$${ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$

Richtig sind demzufolge die Aussagen 1, 2 und 4.

(3)  Man erhält nach einigen Matrizenmultiplikationen:

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0\\ 0 &1 &1 &1\\ 1 &1 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \hspace{0.05cm},\hspace{1cm} { \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T} = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} z_5 \\ z_6 \\ z_7 \end{pmatrix} = \begin{pmatrix} z_5 \\ z_6 \\ z_7 \end{pmatrix} \hspace{0.05cm}.$$

Durch Gleichsetzen folgt $z_{5} = 0, \ z_{6} = 0, \ z_{7} = 1$   ⇒   Lösungsvorschlag 2.

(4)  Der Matrizenvergleich zeigt, dass die ersten drei Spalten von $\boldsymbol{\rm H}$ und $\boldsymbol{\rm H}_{\rm K}$ identisch sind.

• Die vierte Spalte von $\boldsymbol{\rm H}_{\rm K}$ ist gleich der fünften Spalte der Prüfmatrix.
• Daraus folgt für den Vektor $z_{\rm E} = (z_{4}, z_{6}, z_{7})$ und weiter für den Empfangsvektor $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E})$   ⇒   Lösungsvorschlag 1 und 3.

(5)  Analog zur Teilaufgabe (3) erhält man nun:

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} = \begin{pmatrix} 1 &1 &1 &1\\ 0 &1 &1 &0\\ 1 &1 &0 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \hspace{0.05cm},\hspace{1cm} { \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T} = \begin{pmatrix} 0 &0 &0\\ 1 &1 &0\\ 1 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} z_4 \\ z_6 \\ z_7 \end{pmatrix} = \begin{pmatrix} 0 \\ z_4 + z_6 \\ z_4 + z_7 \end{pmatrix} \hspace{0.05cm}.$$

• Setzt man nun die beiden Spaltenvektoren gleich, so erhält man nur mehr zwei Gleichungen für die drei Unbekannten   ⇒   Lösungsvorschlag 4.
• Oder anders ausgedrückt:   Ist die Anzahl der Auslöschungen des BEC–Kanals größer als der Rang der Matrix $\boldsymbol{\rm H}_{\rm E}$, so ergibt sich keine eindeutige Lösung des resultierenden Gleichungssystems.

Codetabelle des systematischen $(7, 4, 3)$–Hamming–Codes

(6)  Zur Lösung dieser Aufgabe beziehen wir uns wieder auf den systematischen Hamming–Code $(7, 4, 3)$ entsprechend der angegebenen Prüfgleichung und der angegebenen Codetabelle.

• Die Informationsbit sind schwarz dargestellt und die Prüfbit rot.
• Die minimale Distanz dieses Codes beträgt $d_{\rm min} = 3$.

Weiter nehmen wir an, dass stets das gelb hinterlegte Codewort $\underline{x} = (1, 1, 0, 1, 0, 0, 1)$ gesendet wurde. Dann gilt:

• Ist die Anzahl  $n_{\rm E}$  der Auslöschungen kleiner als  $d_{\rm min} = 3$, so ist eine Decodierung nach der hier beschriebenen Methode immer möglich   ⇒   siehe beispielsweise Teilaufgabe (1) mit  $n_{\rm E}= 2$.

• Auch für  $n_{\rm E} = d_{\rm min} = 3$  ist manchmal eine Decodierung möglich, wie in der Teilaufgabe (3) gezeigt. In der Codetabelle gibt es nur ein einziges Codewort, das zum Empfangsvektor  $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E})$  passen könnte, nämlich das gelb hinterlegte Codewort  $\underline{x} = (1, 1, 0, 1, 0, 0, 1)$ .

• Dagegen konnte  $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E})$  entsprechend Teilaufgabe (4) nicht decodiert werden. In der Codetabelle erkennt man neben  $(1, 1, 0, 1, 0, 0, 1)$  mit  $(1, 1, 0, 0, 0, 1, 0)$  ein weiteres Codewort (grün hinterlegt), das durch die  $n_{\rm E} = 3$  Auslöschungen bezüglich Bit 4, 6 und 7 zum Empfangswort  $\underline{y}$  wird. Dieser Fall, wenn die  $n_{\rm E} = d_{\rm min}$  Auslöschungen genau die  $d_{\rm min}$  unterschiedlichen Bit zweier Codeworte betreffen, führt zu einer Matrix  $\mathbf{H}_{\rm E}$  mit einem Rang kleiner  $d_{\rm min}$.

• Ist  $\boldsymbol{\rm H}_{\rm E} > d_{\rm min}$, so ist die Anzahl  $n - n_{\rm E}$  der nicht ausgelöschten Bit kleiner als die Anzahl  $k$  der Informationsbit. In diesem Fall kann das Codewort natürlich nicht decodiert werden.

Das heißt:   Zutreffend sind die Aussagen 1, 3 und 4.