Aufgaben:Exercise 2.15: Block Error Probability with AWGN

• Return to book

Unvollständige Ergebnistabelle

Am Beispiel des  $\rm RSC \, (7, \, 3, \, 5)_8$  mit den Parametern

• $n = 7$  (Anzahl der Codesymbole),
• $k =3$  (Anzahl der Informationssymbole),
• $t = 2$  (Korrekturfähigkeit)

soll die Berechnung der Blockfehlerwahrscheinlichkeit beim  Bounded Distance Decoding  (BDD) gezeigt werden. Die entsprechende Gleichung lautet:

$${\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} \ne \underline{u}) = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$

Die Berechnung erfolgt für den  AWGN–Kanal, der durch den Parameter  $E_{\rm B}/N_0$  gekennzeichnet ist.

• Der Quotient  $E_{\rm B}/{N_0}$  lässt sich über die Beziehung

$$\varepsilon = {\rm Q} \big (\sqrt{{2 \cdot R \cdot E_{\rm B}}/{N_0}} \big )$$

in das  BSC–Modell  überführen, wobei  $R$  die Coderate bezeichnet  $($hier:  $R = 3/7)$  und  ${\rm Q}(x)$  das  komplementäre Gaußsche Fehlerintegral  angibt.

• Da aber beim betrachteten Code die Symbole aus  $\rm GF(2^3)$  entstammen, muss das BSC–Modell mit Parameter  $\varepsilon$  ebenfalls noch an die Aufgabenstellung adaptiert werden.
• Für die Verfälschungwahrscheinlichkeit des  $m$–BSC–Modells  gilt, wobei hier  $m = 3$  zu setzen ist (drei Bit pro Codesymbol):

$$\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m \hspace{0.05cm}.$$

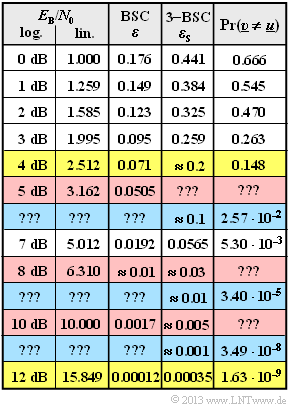
Für einige  $E_{\rm B}/N_0$–Werte sind die Ergebnisse in obiger Tabelle eingetragen. Die beiden gelb hinterlegten Zeilen werden hier kurz erläutert:

• Für  $10 \cdot \lg {E_{\rm B}/N_0} = 4 \ \rm dB$  ergibt sich  $\varepsilon \approx {\rm Q}(1.47) \approx 0.071$  und  $\varepsilon_{\rm S} \approx 0.2$. Die Blockfehlerwahrscheinlichkeit kann hier am einfachsten über das Komplement berechnet werden:

$${\rm Pr(Blockfehler)} = 1 - \left [ {7 \choose 0} \cdot 0.8^7 + {7 \choose 1} \cdot 0.2 \cdot 0.8^6 + {7 \choose 2} \cdot 0.2^2 \cdot 0.8^5\right ] \approx 0.148 \hspace{0.05cm}.$$

• Für  $10 \cdot \lg {E_{\rm B}/N_0} = 12 \ \rm dB$  erhält man  $\varepsilon \approx 1.2 \cdot 10^{-4}$  und  $\varepsilon_{\rm S} \approx 3.5 \cdot 10^{-4}$. Mit dieser sehr kleinen Verfälschungswahrscheinlichkeit dominiert der  $f = 3$–Term, und man erhält:

$${\rm Pr(Blockfehler)} \approx {7 \choose 3} \cdot (3.5 \cdot 10^{-4})^3 \cdot (1- 3.5 \cdot 10^{-4})^4 \approx 1.63 \cdot 10^{-9} \hspace{0.05cm}.$$

• Sie sollen für die rot hinterlegten Zeilen  $(10 \cdot \lg {E_{\rm B}/N_0} = 5 \ \rm dB, \ 8 \ dB$,  $10 \ \rm dB)$  die Blockfehlerwahrscheinlichkeiten berechnen.
• Die blau hinterlegten Zeilen zeigen einige Ergebnisse der  Aufgabe 2.15Z. Dort wird  ${\rm Pr}(\underline{v} ≠ \underline{u})$  für  $\varepsilon_{\rm S} = 10\%,  \ 1\%$  $0.1\%$ berechnet.
• In den Teilaufgaben (4) und (5) sollen Sie den Zusammenhang zwischen der Größe  $\varepsilon_{\rm S}$  und dem AWGN–Parameter  $E_{\rm B}/N_0$  herstellen und somit die obige Tabelle vervollständigen.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Fehlerwahrscheinlichkeit und Anwendungsgebiete.
• Wir verweisen Sie hier auf die beiden interaktive Applets 

Komplementäre Gaußsche Fehlerfunktionen  und 

Binomial- und Poissonverteilung.

Fragebogen

1

Wie groß ist die Blockfehlerwahrscheinlichkeit für  $10 \cdot \lg {E_{\rm B}/N_0} \hspace{0.15cm}\underline{= 5 \ \rm dB}$?

${\rm Pr(Blockfehler)} \ = \ $ $\ \cdot 10^{-2}$

2

Wie groß ist die Blockfehlerwahrscheinlichkeit für  $10 \cdot \lg {E_{\rm B}/N_0} \hspace{0.15cm}\underline{= 8 \ \rm dB}$?

${\rm Pr(Blockfehler)} \ = \ $ $\ \cdot 10^{-4}$

3

Wie groß ist die Blockfehlerwahrscheinlichkeit für  $10 \cdot \lg {E_{\rm B}/N_0}\hspace{0.15cm}\underline{ = 10 \ \rm dB}$?

${\rm Pr(Blockfehler)} \ = \ $ $\ \cdot 10^{-6}$

4

Wie hängt  $\varepsilon_{\rm S} = 0.1$  mit  $10 \cdot \lg {E_{\rm B}/N_0}$  zusammen?   Hinweis:  Verwenden Sie das angegebene Applet zur Berechnung von  ${\rm Q}(x)$.

$\varepsilon_{\rm S} = 10^{-1} \text{:} \hspace{0.4cm} 10 \cdot \lg {E_{\rm B}/N_0} \ = \ $ $\ \rm dB$

5

Ermitteln Sie auch die  $E_{\rm B}/N_0$–Werte  $($in  $\rm dB)$  für  $\varepsilon_{\rm S} = 0.01$  und  $\varepsilon_{\rm S} = 0.001$. Vervollständigen Sie die Tabelle.

$\varepsilon_{\rm S} = 10^{-2} \text{:} \hspace{0.4cm} 10 \cdot \lg {E_{\rm B}/N_0} \ = \ $ $\ \rm dB$

$\varepsilon_{\rm S} = 10^{-3} \text{:} \hspace{0.4cm} 10 \cdot \lg {E_{\rm B}/N_0} \ = \ $ $\ \rm dB$

Musterlösung

Solution

(1)  Aus der Tabelle auf der Angabenseite kann der BSC–Parameter $\varepsilon = 0.0505$ abgelesen werden.

• Damit erhält man für die Symbolverfälschungswahrscheinlichkeit $\varepsilon_{\rm S}$ mit $m = 3$:

$$1 - \varepsilon_{\rm S} = (1 - 0.0505)^3 \approx 0.856 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \varepsilon_{\rm S} \approx 0.144 \hspace{0.05cm}.$$

• Der schnellste Weg zur Berechnung der Blockfehlerwahrscheinlichkeit führt hier über die Formel

$${\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 - {\rm Pr}(f=0) - {\rm Pr}(f=1) - {\rm Pr}(f=2) = 1 - 1 \cdot 0.856^7 - 7 \cdot 0.144^1 \cdot 0.856^6 - 21 \cdot 0.144^2 \cdot 0.856^5$$

$$\Rightarrow \hspace{0.3cm} {\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{v} \ne \underline{u}) =1 - 0.3368 - 0.3965 - 0.2001 \hspace{0.15cm} \underline{=0.0666} \hspace{0.05cm}.$$

(2)  Nach gleichem Rechengang wie in Teilaufgabe (1) ergibt sich mit $\varepsilon_{\rm S} \approx 0.03 \ \Rightarrow \ 1 - \varepsilon_{\rm S} = 0.97$:

$${\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \hspace{-0.05cm}-\hspace{-0.05cm} 1 \cdot 0.97^7 \hspace{-0.05cm}-\hspace{-0.05cm} 7 \cdot 0.03^1 \cdot 0.97^6 \hspace{-0.05cm}-\hspace{-0.05cm} 21 \cdot 0.03^2 \cdot 0.97^5 =1 \hspace{-0.05cm}-\hspace{-0.05cm} 0.8080 \hspace{-0.05cm}-\hspace{-0.05cm} 0.1749\hspace{-0.05cm}-\hspace{-0.05cm} 0.0162= 1 \hspace{-0.05cm}-\hspace{-0.05cm} 0.9991 = 9 \cdot 10^{-4} \hspace{0.05cm}.$$

• Man sieht, dass hier die Differenz zwischen zwei fast gleich großen Zahlen gebildet werden muss, so dass das Ergebnis mit einem Fehler behaftet sein könnte.
• Deshalb berechnen wir noch folgende Größen:

$${\rm Pr}(f=3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 3} \cdot \varepsilon_{\rm S}^3 \cdot (1 - \varepsilon_{\rm S})^4 = 35 \cdot 0.03^3 \cdot 0.97^4 = 8.366 \cdot 10^{-4}\hspace{0.05cm},$$

$${\rm Pr}(f=4) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 4} \cdot \varepsilon_{\rm S}^4 \cdot (1 - \varepsilon_{\rm S})^3 = 35 \cdot 0.03^4 \cdot 0.97^3 = 0.259 \cdot 10^{-4}\hspace{0.05cm},$$

$${\rm Pr}(f=5) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 5} \cdot \varepsilon_{\rm S}^5 \cdot (1 - \varepsilon_{\rm S})^2 = 21 \cdot 0.03^5 \cdot 0.97^2 = 0.005 \cdot 10^{-4}$$

$$\Rightarrow \hspace{0.3cm} {\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} \ne \underline{u}) \approx {\rm Pr}(f=3) + {\rm Pr}(f=4) + {\rm Pr}(f=5) \hspace{0.15cm} \underline{=8.63 \cdot 10^{-4}} \hspace{0.05cm}.$$

• Auf die Terme für $f = 6$ und $f = 7$ kann hier verzichtet werden. Sie liefern keinen relevanten Beitrag.

(3)  Hier ist bereits $\varepsilon_{\rm S} = 0.005 \ \Rightarrow \ 1 - \varepsilon_{\rm S} = 0.995$ in der Tabelle vorgegeben.

• Der (weitaus) dominierende Term bei der Berechnung der Blockfehlerwahrscheinlichkeit ist ${\rm Pr}(f = 3)$:

$${\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} \ne \underline{u}) \approx {\rm Pr}(f=3) = {7 \choose 3} \cdot 0.005^3 \cdot 0.995^4 \hspace{0.15cm} \underline{\approx 4.3 \cdot 10^{-6}} \hspace{0.05cm}.$$

(4)  Für den BSC–Parameter $\varepsilon$ gilt mit $\varepsilon_{\rm S} = 0.1$:

$$\varepsilon = 1 -(1 - \varepsilon_{\rm S})^{1/3} = 1 - 0.9^{1/3} \approx 0.0345 \hspace{0.05cm}.$$

• Der Zusammenhang zwischen $\varepsilon$ und $E_{\rm B}/N_0$ lautet:

$$\varepsilon = {\rm Q}(x)\hspace{0.05cm}, \hspace{0.5cm} x = \sqrt{2 \cdot R \cdot E_{\rm B}/N_0}\hspace{0.05cm}.$$

• Die Inverse $x = {\rm Q}^{-1}(0.0345)$ ergibt sich mit dem Applet Komplementäre Gaußsche Fehlerfunktionen zu $x = 1.82$.
• Damit erhält man weiter:

$$E_{\rm B}/N_0 = \frac{x^2}{2R} = \frac{1.82^2}{2R \cdot 3/7} \approx 3.864 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}(E_{\rm B}/N_0) \hspace{0.15cm} \underline{\approx 5.87 \,\, {\rm dB}} \hspace{0.05cm}.$$

(5)  Nach gleicher Rechnung erhält man

• für $\varepsilon_{\rm S} = 10^{-2} \ \Rightarrow \ \varepsilon \approx 0.33 \cdot 10^{-2} \ \Rightarrow \ x = {\rm Q}^{-1}(\varepsilon) = 2.71$

$$E_{\rm B}/N_0 = \frac{x^2}{2R} = \frac{2.71^2}{2R \cdot 3/7} \approx 8.568 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}(E_{\rm B}/N_0) \hspace{0.15cm} \underline{\approx 9.32 \,\, {\rm dB}} \hspace{0.05cm},$$

• für $\varepsilon_{\rm S} = 10^{-3} \ \Rightarrow \ \varepsilon \approx 0.33 \cdot 10^{-3} \ \Rightarrow \ x = {\rm Q}^{-1}(\varepsilon) = 3.4$:

$$E_{\rm B}/N_0 = \frac{x^2}{2R} = \frac{3.4^2}{2R \cdot 3/7} \approx 13.487 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}(E_{\rm B}/N_0) \hspace{0.15cm} \underline{\approx 11.3 \,\, {\rm dB}} \hspace{0.05cm}.$$

Ergebnisse zur $\rm RSC \, (7, \, 3, \, 5)_8$–Decodierung

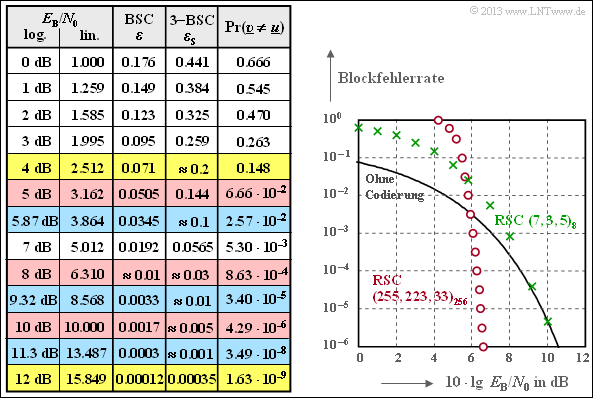
Die Grafik zeigt den Verlauf der Blockfehlerwahrscheinlichkeit in Abhängigkeit von $10 \cdot \lg {E_{\rm B}/N_0}$ sowie die vollständig ausgefüllte Ergebnistabelle.

Man erkennt das deutlich ungünstigere (asymptotische) Verhalten dieses kurzen (grünen) Codes $\rm RSC \, (7, \, 5, \, 3)_8$ gegenüber dem (roten) Vergleichscode $\rm RSC \, (255, \, 223, \, 33)_8$:

• Für Abszissenwerte kleiner als $10 \ \rm dB$ ergibt sich sogar ein schlechteres Ergebnis als ohne Codierung.
• Deshalb soll hier nochmals darauf hingewiesen werden, dass dieser $\rm RSC \, (7, \, 3, \, 5)_8$ wenig praktische Bedeutung hat.
• Er wurde für diese Aufgabe nur deshalb ausgewählt, um mit vertretbarem Aufwand die Berechnung der Blockfehlerwahrscheinlichkeit bei Bounded Distance Decoding (BDD) demonstrieren zu können.