Applets:Zur Verdeutlichung der grafischen Faltung

Open Applet in a new tab

Programmbeschreibung

Dieses Applet verdeutlicht die Quellencodierverfahren nach Huffman bzw. Shannon–Fano. Diese Verfahren komprimieren redundante wertdiskrete Quellen ohne Gedächtnis mit Stufenzahl  $M$, dem Symbolvorrat  $\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \} = \{ \rm A, \hspace{0.1cm} B, \hspace{0.1cm}\text{ ...}\}$ und den Symbolwahrscheinlichkeiten  $p_{\rm A} \hspace{0.05cm},\hspace{0.1cm} p_{\rm B} \hspace{0.05cm}, \hspace{0.05cm}\text{ ...}$ .

Ziel der Quellencodierung und insbesondere der Klasse der Entropiecodierung – zu der „Huffman” und „Shannon–Fano” gehören – ist, dass die mittlere Codewortlänge  $L_{\rm M}$  des binären Codes – darstellbar durch unterschiedlich lange Folgen von Nullen und Einsen – möglichst nahe an die Quellenentropie

$$H = \sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\mu})} = -\sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}{\rm Pr}(q_{\mu})\hspace{0.5cm}\big[\hspace{0.05cm}{\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Quellensymbol}\hspace{0.05cm}\big]$$

heranreicht. Allgemein gilt  $L_{\rm M} \ge H$, wobei das Gleichheitszeichen nicht für alle Symbolwahrscheinlichkeiten erreicht werden kann.

Dargestellt werden jeweils

• das Baumdiagramm zur Herleitung des jeweiligen Binärcodes, und
• eine simulierte Quellensymbolfolge der Länge  $N = 10000$  (Entropie  $H\hspace{0.05cm}' \approx H)$  und die dazugehörige Codesymbolfolge der Länge  $L_{\rm M}\hspace{0.05cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} N$.

Auf die Einheiten „$\rm bit/Quellensymbol$” für die Entropie und die mittlere Codewortlänge wird im Programm verzichtet.

Theoretischer Hintergrund

Faltung im Zeitbereich

Der  Faltungssatz  ist mit das wichtigste Gesetz der Fouriertransformation. Wir betrachten zunächst den Faltungssatz im Zeitbereich und setzen voraus, dass die Spektren zweier Zeitfunktionen $x_1(t)$ und $x_2(t)$ bekannt sind:

$$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$

Dann gilt für die Zeitfunktion des Produktes $X_1(f) \cdot X_2(f)$:

$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$

Hierbei ist $\tau$ eine formale Integrationsvariable mit der Dimension einer Zeit.

$\text{Definition:}$  Die obige Verknüpfung der Zeitfunktion $x_1(t)$ und $x_2(t)$ bezeichnet man als Faltung und stellt diesen Funktionalzusammenhang mit einem Stern dar:

$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$

Damit lässt sich obige Fourierkorrespondenz auch wie folgt schreiben:

$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$

$\text{Beweis}$

Anmerkung:   Die Faltung ist kommutativ   ⇒   Die Reihenfolge der Operanden ist vertauschbar:   ${ {x}}_{\rm{1}} ( t ) * { {x}}_{\rm{2}} (t ) ={ {x}}_{\rm{2}} ( t ) * { {x}}_{\rm{1}} (t )$.

Zur Berechnung von Signal und Spektrum am LZI–Ausgang

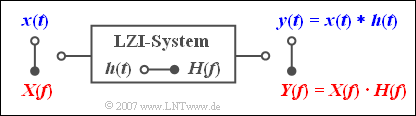
$\text{Beispiel 1:}$  Ein jedes lineare zeitinvariante (LZI-) System kann sowohl durch den Frequenzgang $H(f)$ als auch durch die Impulsantwort $h(t)$ beschrieben werden, wobei der Zusammenhang zwischen diesen beiden Systemgrößen ebenfalls durch die Fouriertransformation gegeben ist.

Legt man an den Eingang ein Signal $x(t)$ mit dem Spektrum $X(f)$ an, so gilt für das Spektrum des Ausgangssignals:

$$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$

Mit dem Faltungssatz ist es nun möglich, das Ausgangssignal auch direkt im Zeitbereich zu berechnen:

$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$

Aus dieser Gleichung geht nochmals hervor, dass die Faltungsoperation kommutativ  ist.

Faltung im Frequenzbereich

Die Dualität zwischen Zeit– und Frequenzbereich erlaubt auch Aussagen hinsichtlich des Spektrums des Produktsignals:

$$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$

Dieses Resultat lässt sich ähnlich wie der Faltungssatz im Zeitbereich beweisen. Die Integrationsvariable $\nu$ hat aber nun die Dimension einer Frequenz.

Faltung im Frequenzbereich

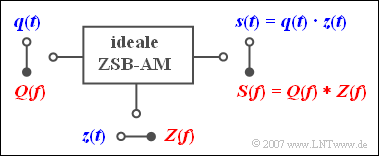
$\text{Beispiel 2:}$  Die Zweiseitenband-Amplitudenmodulation (ZSB-AM) ohne Träger wird durch das skizzierte Modell beschrieben.

• Bei der Zeitbereichsdarstellung (blau) ergibt sich das modulierte Signal $s(t)$ als das Produkt aus dem Nachrichtensignal $q(t)$ und dem (normierten) Trägersignal $z(t)$.
• Nach dem Faltungssatz folgt daraus für den Frequenzbereich (rot), dass das Ausgangsspektrum $S(f)$ gleich dem Faltungsprodukt aus $Q(f)$ und $Z(f)$ ist.

Faltung einer Funktion mit einer Diracfunktion

Sehr einfach wird die Faltungsoperation, wenn einer der beiden Operanden eine Diracfunktion ist. Dies gilt für die Faltung im Zeit– und im Frequenzbereich gleichermaßen.

Wir betrachten beispielhaft die Faltung einer Funktion $x_1(t)$ mit der Funktion

$$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T}.$$

Für die Spektralfunktion des Signals $y(t) = x_1(t) \ast x_2(t)$ gilt dann:

$$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T} .$$

Die komplexe Exponentialfunktion führt zur Verschiebung um $T$  ⇒  Verschiebungssatz, der Faktor $\alpha$ zu einer Dämpfung ($\alpha < 1$) bzw. Verstärkung ($\alpha > 1$ ). Daraus folgt:

$$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$

$\text{In Worten: }$  Die Faltung einer beliebigen Funktion mit einer Diracfunktion bei $t = T$ ergibt die um $T$ nach rechts verschobene Funktion, wobei noch die Gewichtung der Diracfunktion durch den Faktor $\alpha$ zu berücksichtigen ist.

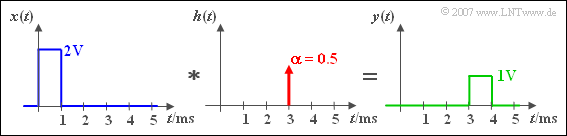
$\text{Beispiel 3:}$  Ein Rechtecksignal $x(t)$ wird durch ein LZI-System um eine Laufzeit $\tau = 3\,\text{ ms}$ verzögert und um den Faktor $\alpha = 0.5$ gedämpft.

Faltung eines Rechtecks mit einer Diracfunktion

Verschiebung und Dämpfung erkennt man sowohl am Ausgangssignal $y(t)$ als auch an der Impulsantwort $h(t)$.

Grafische Faltung

Für die Beschreibungen auf dieser Seite wird von folgender Faltungsoperation ausgegangen:

Bildschirmabzug des Programms „Grafische Faltung”

$$y(t) = x_1 (t) * x_2 (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$

Die Lösung des Faltungsintegrals soll auf grafischem Wege erfolgen. Es wird vorausgesetzt, dass $x_1(t)$ und $x_2(t)$ zeitkontinuierliche Signale sind.

Dann sind die folgenden Schritte erforderlich:

1.   Die Zeitvariablen der beiden Funktionen ändern:  
       $x_1(t) \to x_1(\tau)$,   $x_2(t) \to x_2(\tau)$.
2.   Zweite Funktion spiegeln:   $x_2(\tau) \to x_2(-\tau)$.
3.   Gespiegelte Funktion um $t$ verschieben:   $x_2(-\tau) \to x_2(t-\tau)$.
4.   Multiplikation der beiden Funktionen $x_1(\tau)$ und $x_2(t-\tau)$.
5.   Integration über das Produkt bezüglich $\tau$ in den Grenzen von $-\infty$ bis $+\infty$.

Da die Faltung kommutativ ist, kann anstelle von $x_2(\tau)$ auch $x_1(\tau)$ gespiegelt werden.

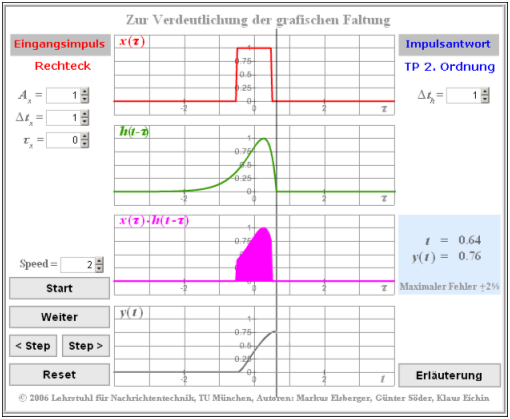
Die Thematik wird auch durch das Interaktionsmodul Zur Verdeutlichung der grafischen Faltung veranschaulicht. Nebenstehende Grafik zeigt einen Bildschirmabzug.

Beispiel einer Faltungsoperation:
Sprungfunktion gefaltet mit Exponentialfunktion

$\text{Beispiel 4:}$  Die Vorgehensweise bei der grafischen Faltung wird nun anhand eines ausführlichen Beispiels erklärt:

• Am Eingang eines Filters liege eine Sprungfunktion $x(t) = \gamma(t)$ an.
• Die Impulsantwort des RC-Tiefpasses sei $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$

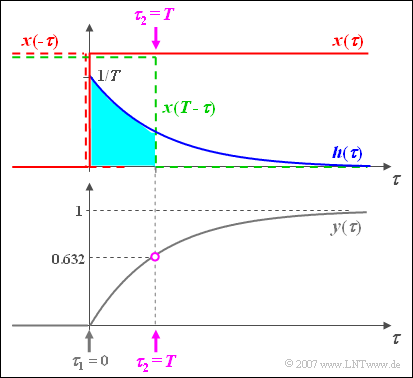
Die Grafik zeigt rot das Eingangssignal $x(\tau)$, blau die Impulsantwort $h(\tau)$ und grau das Ausgangssignal $y(\tau)$. Die Zeitachse ist bereits in $\tau$ umbenannt.

Das Ausgangssignal kann zum Beispiel nach folgender Gleichung berechnet werden:

$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$

Noch einige Anmerkungen zur grafischen Faltung:

• Der Ausgangswert bei $t = 0$ ergibt sich, indem man das Eingangssignal $x(\tau)$ spiegelt, dieses gespiegelte Signal $x(-\tau)$ mit der Impulsantwort $h(\tau)$ multipliziert und darüber integriert.
• Da es hier kein Zeitintervall gibt, bei dem sowohl die blaue Kurve $h(\tau)$ und gleichzeitig auch die rot gestrichelte Spiegelung $x(-\tau)$ ungleich Null ist, folgt daraus $y(t=0)=0$.
• Für jeden anderen Zeitpunkt $t$ muss das Eingangssignal verschoben werden   ⇒   $x(t-\tau)$, beispielsweise entsprechend der grün gestrichelten Kurve für $t=T$.
• Da in diesem Beispiel auch $x(t-\tau)$ nur die Werte $0$ oder $1$ annehmen kann, wird die Integration (allgemein von $\tau_1$ bis $\tau_2$) sehr einfach und man erhält hier mit $\tau_1 = 0$ und $\tau_2 = t$ :

$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$

Die Skizze gilt für $t=T$ und führt zum Ausgangswert $y(t=T) = 1 – 1/\text{e} \approx 0.632$.

Versuchsdurchführung

• Wählen Sie zunächst die Aufgabennummer. Eine Aufgabenbeschreibung wird angezeigt.
• Alle Parameter sind angepasst. Alle Grafiken und Ergebniswerte sind aktualisiert.
• Musterlösung nach Drücken des entsprechenden Buttons.
• Nummer „0”:   Gleiche Einstellung wie beim Programmstart.

(1)   Wählen Sie die Parameter gemäß Voreinstellung  $\text{(Gaußimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 1; \text{ Impulsantwort gemäß Tiefpass 2. Ordnung: }\Delta t_h= 1)$.
         Interpretieren Sie die dargestellten Grafiken. Wie groß ist der maximale Ausgangswert  $y_{\rm max}$? Zu welcher Zeit  $t_{\rm max}$  tritt dieser auf?

•  Nach Umbenennung:  Eingangssignal  $x(\tau)$   ⇒   rote Kurve,  Impulsantwort  $h(\tau)$   ⇒   blaue Kurve, nach Spiegelung  $h(-\tau)$   ⇒   grüne Kurve.
•  Verschiebt man die grüne Kurve um  $t$  nach rechts, so erhält man $h(t-\tau)$. $y(t)$  ergibt sich durch Multiplikation und Integration bzgl. $\tau$:

$$y (t) = \int_{ - \infty }^{ +\infty } {x ( \tau ) } \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ t } {x ( \tau ) } \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau .$$

•  Der Ausgangsimpuls  $y_(t)$  ist im vorliegenden Fall unsymmetrisch; der maximale Ausgangswert  $y_{\rm max}\approx 0.67$  tritt bei  $t_{\rm max}\approx 1.5$  auf.

(2)   Was ändert sich, wenn man die äquivalente Impulsdauer von  $h(t)$  auf  $\Delta t_h= 1.5$  erhöht?

•  $y_{\rm max}\approx 0.53$  tritt nun bei  $t_{\rm max}\approx 1.75$  auf. Durch die ungünstigere Impulsantwort wird der Eingangsimpuls stärker verformt.
•  Bei einem digitalen Nachrichtenübertragungssystem hätte dies stärkere Impulsinterenzen (Intersymbol Interference ) zur Folge.

(3)   Wählen Sie nun den symetrischen  $\text{Rechteckimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$  und die  $\text{Impulsantwort gemäß Spalt–Tiefpass: }\Delta t_h= 1$.
         Interpretieren Sie das Faltungsergebnis. Wie groß ist der maximale Ausgangswert  $y_{\rm max}$? Zu welchen Zeiten ist  $y(t)>0$? Beschreibt  $h(t)$  ein kausales System?

•  Die Faltung zweier Rechtecke mit jeweiliger Dauer  $1$  ergibt ein Dreieck mit absoluter Dauer  $2$  ⇒   äquivalente Impulsdauer  $\Delta t_y= 1$.
•  $y(t)$  ist im Bereich von  $-0.5$  bis  $+1.5$  von Null verschieden. Impulsmaximum  $y_{\rm max} = 1$  bei  $t_{\rm max} = +0.5$.
•  $h(t)$  beschreibt ein kausales System, da  $h(t) \equiv 0$  für  $t < 0$  ⇒   die „Wirkung”  $y(t)$  kommt nicht vor der „Ursache”  $x(t)$.

(4)   Was ändert sich, wenn man die äquivalente Impulsdauer von  $h(t)$  auf  $\Delta t_h= 2$  erhöht?

•  Die Faltung zweier unterschiedlich breiten Rechtecke ergibt ein Trapez, hier zwischen  $-0.5$  und  $+2.5$ ⇒   äquivalente Impulsdauer  $\Delta t_y= 2$.
•  Das Maximum  $y_{\rm max} = 0.5$  tritt im Bereich  $0.5 \le t \le 1.5$ auf. Bezüglich der Kausalität ändert sich nichts.

(5)   Wählen Sie nun den (unsymetrischen)  $\text{Rechteckimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0.5$  und die  $\text{ Impulsantwort eines Tiefpasses 1. Ordnung: }\Delta t_h= 1$.
         Interpretieren Sie die Ergebnisse. Wie groß ist  $y_{\rm max}$? Zu welchen Zeiten ist  $y(t)>0$ ? Beschreibt  $h(t)$  ein kausales System?

•  $h(t)$  hat für  $t > 0$  einen exponentiell abfallenden Verlauf. Für  $t > 0$  gilt stets  $y(t) > 0$, aber die Signalwerte können sehr klein werden.
•  $y_{\rm max} = 0.63$  tritt bei  $t_{\rm max} = +1$ auf. Für  $t < t_{\rm max}$ ist der Verlauf exponentiell ansteigend, für  $t > t_{\rm max}$  exponentiell abfallend.
•  Der Tiefpass 1. Ordnung kann mit einem Widerstand und einer Kapazität realisiert werden. Jedes realisierbare System ist per se kausal.

(6)   Wählen Sie wie in  (3)  die rechteckförmige Impulsantwort  $\text{(Spalt–Tiefpass; }\Delta t_h= 1)$. Mit welchem  $x(t)$  ergibt sich das gleiche  $y(t)$  wie bei  (5)?

•  Das Signal  $y(t)$  in  (5)  ergab sich als Faltung zwischen dem rechteckigen Eingang  $x(t)$  und der Exponentialfunktion  $h(t)$.
•  Da die Faltungsoperation kommutativ ist, ergibt sich das gleiche Ergebnis mit der Exponentialfunktion  $x(t)$ und der Rechteckfunktion  $h(t)$.
•  Die richtige Einstellung für das Eingangssignal  $x(t)$  ist somit  $\text{Exponentialimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ .

(7)   Für den Rest dieser Versuchsdurchführung betrachten wir stets den Gauß–Tiefpass. Die äquivalente Dauer der Impulsantwort  $h(t)$  sei zunächst  $\Delta t_h= 0.8$.
         Analsyieren und interpretieren Sie dieses „System” im Hinblick auf Kausalität und die entstehenden Verzerrungen für ein Rechtecksignal.

•  Der Tiefpass ist nicht kausal (realisierbar): für  $t < 0$  gilt nicht  $h(t) \equiv 0$  gilt. Geeignetes Modell, wenn man die unendliche Laufzeit außer Acht lässt.
•  Je größer  $\Delta t_h$  ist, desto breiter wird der Ausgangsimpuls und um so stärker die Degradation eines Digitalsystems durch Impulsinterferenzen.
•  Der Tiefpass–Frequenzgang  $H(f)$  ist die Fouriertransformierte von  $h(t)$. Je größer  $\Delta t_h$  ist, desto kleiner ist  $\Delta f_h = 1/\Delta t_h$.

(8)   Wählen Sie nun den  $\text{Gaußimpuls: }A_x = 1, \ \Delta t_x= 1.5, \ \tau_x = 0$  und den  $\text{Gauß–Tiefpass: }\Delta t_h= 2$. Welche Form hat der Ausgangsimpuls  $y(t)$?
         Wie groß ist die äquivalente Dauer  $\Delta t_y$  des Ausgangsimpulses und der maximale Ausgangswert  $y_{\rm max}$? Zu welcher Zeit  $t_{\rm max}$  tritt dieser auf?

•  $y(t)$  ist ebenfalls (exakt) gaußförmig. Merksatz:  Gauß gefaltet mit Gauß ergibt immer Gauß.
•  Äquivalente Dauer:  $\Delta t_y =\sqrt{\Delta t_x^2+ \Delta t_h^2} = 2.5$. Impulsmaximum $($bei $t=0)$:  $y_{\rm max} = A_x \cdot \Delta t_x/\Delta t_y = 1 \cdot 1.5/2.5 = 0.6$.

(9)   Wählen Sie nun den  $\text{Dreieckimpuls: }A_x = 1, \ \Delta t_x= 1.5, \ \tau_x = 0$  und den  $\text{Gauß–Tiefpass: }\Delta t_h= 2$. Welche Form hat der Ausgangsimpuls  $y(t)$?
         Wie groß ist die äquivalente Dauer  $\Delta t_y$  des Ausgangsimpulses und der maximale Ausgangswert  $y_{\rm max}$? Zu welcher Zeit  $t_{\rm max}$  tritt dieser auf?

•  $y(t)$  ist gaußähnlich, aber nicht exakt gaußförmig. Merksatz:  Gauß gefaltet mit Nicht–Gauß ergibt niemals exakt Gauß.
•  Die abgefragten Kenngrößen des Ausgangsimpules  $y(t)$  unterscheiden sich nur geringfügig gegenüber  (8):  $\Delta t_y \approx 2.55$,  $y_{\rm max} \approx 0.59$.

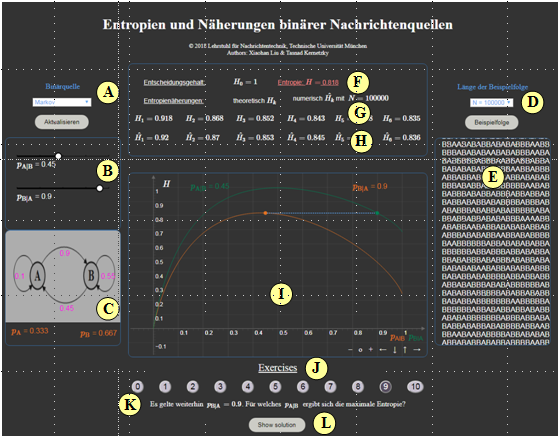
Zur Handhabung des Applets

    (A)     Auswahl:   Gedächtnislose Quelle / Markovquelle

    (B)     Parametereingabe per Slider (Beispiel Markovquelle)

    (C)     Markovdiagramm (falls Markovquelle)

    (D)     Eingabe der Folgenlänge  $N$  zur Berechnung der  $\hat H_k$

    (E)     Ausgabe einer simulierten Symbolfolge

    (F)     Ausgabe des Entropiewertes  $H$

    (G)     Ausgabe der Entropienäherungen  $H_k$

    (H)     Ausgabe der numerisch ermittelten Entropienäherungen  $\hat H_k$

    (I)     Grafikfeld zur Darstellung der Funktion  $H(p_{\rm A})$  bzw.  $H(p_{\rm A}|p_{\rm B})$

    (J)     Bereich für die Versuchsdurchführung:   Aufgabenauswahl

    (K)     Bereich für die Versuchsdurchführung:   Aufgabenstellung

    (L)     Bereich für die Versuchsdurchführung:   Musterlösung

Über die Autoren

Dieses interaktive Applet wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

• Die erste Version wurde 2006 von  Markus Elsberger  im Rahmen seiner Bachelorarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
• 2019 wurde das Programm von  Carolin Mirschina  im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).

Die Umsetzung dieses Applets auf HTML 5 wurde durch  Studienzuschüsse  der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Open Applet in a new tab