Difference between revisions of "Examples of Communication Systems/Radio Interface"
| Line 134: | Line 134: | ||
==Modulation bei GSM–Systemen== | ==Modulation bei GSM–Systemen== | ||
<br> | <br> | ||
| − | Entsprechend den Aussagen der letzten | + | Entsprechend den Aussagen der letzten Seiten müssen in einem Frequenzkanal $156.25$ Bit pro Zeitschlitz $(0.5769 \ \rm ms)$ übertragen werden. Dies entspricht einer Gesamtbitrate (für acht TDMA–Nutzer inkl. Kanalcodierung, Signalisierungs– und Synchronisationsinformation, etc.) von $R_{\rm ges} = 270\hspace{0.08cm}833 \ \rm bit/s$. |
| − | + | Für diese Bitrate steht bei GSM eine Bandbreite von $B = 200 \ \rm kHz$ zur Verfügung. Man benötigt deshalb ein Modulationsverfahren mit einer Bandbreiteneffizienz von mindestens $β =R_{\rm ges}/B = 1.35$. | |
| − | |||
| − | |||
| − | |||
| − | :$$\int^{T} _{0} \cos (2 \pi t \cdot (f_{\rm T}+ \Delta f_{\rm A} ))\cdot \cos (2 \pi t \cdot (f_{\rm T}- \Delta f_{\rm A} ))\,{\rm | + | Beim GSM–Mobilfunk findet das Modulationsverfahren '''Gaussian Minimum Shift Keying''' (GMSK) Anwendung. Dieses wurde schon im Kapitel [[Modulationsverfahren/Nichtlineare_digitale_Modulation#GMSK_.E2.80.93_Gaussian_Minimum_Shift_Keying|Nichtlineare digitale Modulation]] des Buches „Modulationsverfahren” ausführlich behandelt. Hier folgt eine kurze, stichpunktartige Beschreibung: |
| + | *GMSK ist eine abgewandelte Form von '''Frequency Shift Keying''' (FSK). Diese ergibt sich, wenn man einen [[Modulationsverfahren/Frequenzmodulation_(FM)#Realisierung_eines_FM.E2.80.93Modulators|Frequenzmodulator]] mit einem binären bipolaren rechteckförmigen Eingangssignal betreibt. | ||
| + | *Ein solches FSK-Signal $s(t)$ beinhaltet innerhalb einer jeden Symboldauer $T$ jeweils nur eine einzige Augenblicksfrequenz $f_{\rm A}(t) = \rm const.$ Ist das (normierte) Eingangssignal gleich $+1$, so ist $f_{\rm A}(t)$ gleich der Summe aus der Trägerfrequenz $f_{\rm T}$ und dem Frequenzhub $Δf_{\rm A}$. Entsprechend gilt für den Amplitudenwert $-1$: $f_{\rm A}(t) = f_{\rm T} - Δf_{\rm A}$. | ||
| + | *Um eine einfache Demodulation zu ermöglichen, sollten die beiden Signale mit den Frequenzen $f_{\rm T} ± Δf$ innerhalb der Symboldauer $T$ orthogonal zueinander sein. Demzufolge muss gelten: | ||
| + | |||
| + | :$$\int^{T} _{0} \cos \big(2 \pi t \cdot (f_{\rm T}+ \Delta f_{\rm A} )\big)\cdot \cos \big(2 \pi t \cdot (f_{\rm T}- \Delta f_{\rm A} )\big)\,{\rm | ||
d}t= 0\hspace{0.05cm}. $$ | d}t= 0\hspace{0.05cm}. $$ | ||
| − | :Daraus ergibt sich für den '''Frequenzhub''' die Anforderung: | + | :Daraus ergibt sich für den '''Frequenzhub''' die Anforderung: |
:$$\Delta f_{\rm A} = \frac{k}{4 \cdot T}\hspace{0.2cm}{\rm | :$$\Delta f_{\rm A} = \frac{k}{4 \cdot T}\hspace{0.2cm}{\rm | ||
mit}\hspace{0.2cm}k = 1, 2, 3, \text{...}$$ | mit}\hspace{0.2cm}k = 1, 2, 3, \text{...}$$ | ||
| − | *Da bei FSK–Systemen der '''Modulationsindex''' zu $h = 2 · Δf_{\rm A} · T$ definiert ist, folgt $h = k/2$. Der kleinste Wert unter Einhaltung der Orthogonalitätsbedingungen ist somit $h_{\rm min} = 0.5$. | + | *Da bei FSK–Systemen der '''Modulationsindex''' zu $h = 2 · Δf_{\rm A} · T$ definiert ist, folgt $h = k/2$. Der kleinste Wert unter Einhaltung der Orthogonalitätsbedingungen ist somit $h_{\rm min} = 0.5$. |
| − | *Ein FSK–System mit $h = 0.5$ bzw. $Δf_{\rm A}$ = $ | + | *Ein FSK–System mit $h = 0.5$ bzw. $Δf_{\rm A}$ = ${1}/{4T}$ bezeichnet man als [[Modulationsverfahren/Nichtlineare_digitale_Modulation#MSK_.E2.80.93_Minimum_Shift_Keying|Minimum Shift Keying]] – kurz MSK. Dieses wird in allen GSM-Systemen eingesetzt, da ein größerer Modulationindex als $h = 0.5$ eine deutlich größere Bandbreite beanspruchen würde. |
| − | *Ein sehr schmales Spektrum ergibt sich allerdings nur dann, wenn an den Symbolgrenzen Phasensprünge durch Phasenwertanpassung vermieden werden. MSK gehört somit zu den ''Continuous Phase Frequency Shift Keying''–Verfahren (CP–FSK, siehe nächste Seite). | + | *Ein sehr schmales Spektrum ergibt sich allerdings nur dann, wenn an den Symbolgrenzen Phasensprünge durch Phasenwertanpassung vermieden werden. MSK gehört somit zu den ''Continuous Phase Frequency Shift Keying''–Verfahren ('''CP–FSK''', siehe nächste Seite). |
| − | *Vor dem Frequenzmodulator wird zusätzlich noch ein Tiefpass mit Gauß–Charakteristik eingefügt, wodurch die GSM–Bandbreite weiter verringert wird. Man nennt diese Modulationsart [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle#Gaussian_Minimum_Shift_Keying_.28GMSK.29|Gaussian Minimum Shift Keying]] (GMSK). | + | *Vor dem Frequenzmodulator wird zusätzlich noch ein Tiefpass mit Gauß–Charakteristik eingefügt, wodurch die GSM–Bandbreite weiter verringert wird. Man nennt diese Modulationsart [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle#Gaussian_Minimum_Shift_Keying_.28GMSK.29|Gaussian Minimum Shift Keying]] ('''GMSK'''). |
==Kontinuierliche Phasenanpassung bei FSK == | ==Kontinuierliche Phasenanpassung bei FSK == | ||
<br> | <br> | ||
| − | Ausgehend vom Rechtecksignal $q(t)$ und der Trägerfrequenz $f_{\rm T} = 4/T$ betrachten wir die FSK–Signale $s_{\rm A}(t)$, ... , $s_{\rm D}(t)$ bei unterschiedlichem Frequenzhub $Δf_{\rm A}$ ⇒ Modulationindex $h = 2 · Δf_{\rm A} · T$. | + | Ausgehend vom Rechtecksignal $q(t)$ und der Trägerfrequenz $f_{\rm T} = 4/T$ betrachten wir die FSK–Signale $s_{\rm A}(t)$, ... , $s_{\rm D}(t)$ bei unterschiedlichem Frequenzhub $Δf_{\rm A}$ ⇒ Modulationindex $h = 2 · Δf_{\rm A} · T$. |
[[File:P_ID1197__Bei_T_3_2_S7_v2.png|center|frame|Beispielhafte Signale zur kontinuierlichen Phasenanpassung]] | [[File:P_ID1197__Bei_T_3_2_S7_v2.png|center|frame|Beispielhafte Signale zur kontinuierlichen Phasenanpassung]] | ||
| − | Zu den Signalverläufen ist anzumerken (wir verweisen auch auf das interaktive Applet [[Applets:Frequency_Shift_Keying_%26_Continuous_Phase_Modulation|Frequency Shift Keying & Continuous Phase Modulation]]): | + | Zu den Signalverläufen ist anzumerken (wir verweisen auch auf das interaktive Applet [[Applets:Frequency_Shift_Keying_%26_Continuous_Phase_Modulation|Frequency Shift Keying & Continuous Phase Modulation]]): |
| − | *Das Signal $s_{\rm A}(t)$ ergibt sich mit $Δf_{\rm A} = 1/T$ ⇒ | + | *Das Signal $s_{\rm A}(t)$ ergibt sich mit $Δf_{\rm A} = 1/T$ ⇒ Modulationsindex $h = 2$. Man erkennt die höhere Frequenz $f_1 = 5/T$ $($für $a_ν = +1)$ gegenüber der Frequenz $f_2 = 3/T$ $($für $a_ν = -1)$. |
| − | *Mit $Δf_{\rm A} = 0.5/T$ (Signal $s_{\rm {\rm B}}(t)$, $h = 1$ | + | *Mit $Δf_{\rm A} = 0.5/T$ $($Signal $s_{\rm {\rm B}}(t)$, $h = 1)$ gilt $f_1 = 4.5/T$ und $f_2 = 3.5/T$. An jeder Symbolgrenze tritt ein Phasensprung um $π$ auf, wenn keine Phasenanpassung wie beim Signal $s_{\rm C}(t)$ vorgenommen wird. |
| − | *Bei $s_{\rm C}(t)$ wird im Bereich $0$ ... $T$ der Koeffizient $a_1 = +1$ durch $\cos(2π·f_1·t)$ repräsentiert, während der ebenfalls positive Koeffizient $a_2 = +1$ im Bereich $T$ ... $2T$ zum Signal $-\cos(2π·f_1\hspace{0.01cm}·\hspace{0.01cm}(t-T))$ führt. Durch diese Anpassung werden somit Phasensprünge vermieden. | + | *Bei $s_{\rm C}(t)$ wird im Bereich $0$ ... $T$ der Koeffizient $a_1 = +1$ durch $\cos(2π·f_1·t)$ repräsentiert, während der ebenfalls positive Koeffizient $a_2 = +1$ im Bereich $T$ ... $2T$ zum Signal $-\cos(2π·f_1\hspace{0.01cm}·\hspace{0.01cm}(t-T))$ führt. Durch diese Anpassung werden somit Phasensprünge vermieden. |
| − | *Das Signal $s_{\rm D}(t)$ beschreibt das MSK-Signal (Frequenzhub $Δf_{\rm A} = 0.25/T$ ⇒ Modulationsindex $h = 0.5$ | + | *Das Signal $s_{\rm D}(t)$ beschreibt das MSK-Signal $($Frequenzhub $Δf_{\rm A} = 0.25/T$ ⇒ Modulationsindex $h = 0.5)$, ebenfalls mit Phasenanpassung. Hier sind bei jeder Symbolgrenze – je nach den vorherigen Symbolen – vier unterschiedliche Anfangsphasen möglich. |
| − | *Bei $\rm GSM \ 900$ beträgt die Trägerfrequenz $f_{\rm T} | + | *Bei $\rm GSM \ 900$ beträgt die Trägerfrequenz $f_{\rm T} = 900\ \rm MHz$ und die Symboldauer ist $T ≈ 3.7 \ \rm µ s$. Mit dem Modulationsindex $h = 0.5$ ergibt sich $Δf_{\rm A} ≈ 68 \ \rm kHz$. Die beiden Frequenzen $f_1 = 900.068\ \rm MHz$ und $f_2 = 899.932 \ \rm MHz$ liegen somit sehr eng beieinander. |
Revision as of 12:14, 8 August 2019
Contents
- 1 Logische Kanäle von GSM
- 2 Uplink– und Downlink–Parameter
- 3 Realisierung von FDMA und TDMA
- 4 Die verschiedenen Burstarten bei GSM
- 5 GSM–Rahmenstruktur
- 6 Modulation bei GSM–Systemen
- 7 Kontinuierliche Phasenanpassung bei FSK
- 8 Minimum Shift Keying (MSK)
- 9 Gaussian Minimum Shift Keying (GMSK)
- 10 Vor– und Nachteile von GMSK
- 11 Radio Subsystem Link Control
- 12 Aufgaben zum Kapitel
- 13 Quellenverzeichnis
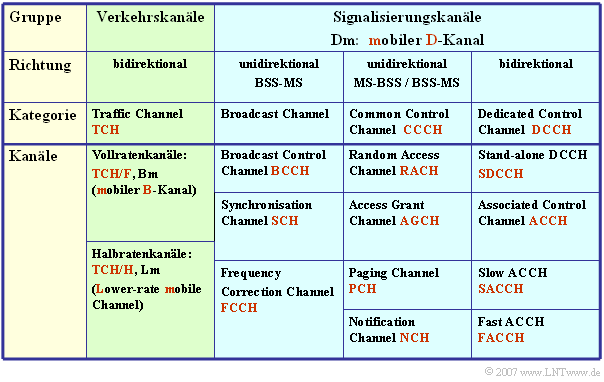
Logische Kanäle von GSM
Entscheidend für den ordnungsgemäßen Betrieb des GSM–Netzes und den Informationsaustausch zwischen Mobil– und Basisstation ist die Funkschnittstelle. Diese wird auch „Luftschnittstelle” oder „Physical Layer” genannt und definiert alle physikalischen Kanäle des GSM–Systems sowie deren Zuordnung zu den logischen Kanälen. Weiterhin ist die Funkschnittstelle für weitere Funktionalitäten wie zum Beispiel das Radio Subsystem Link Control zuständig.
Beginnen wir mit den logischen Kanälen. Diese können entweder einen ganzen physikalischen Kanal oder auch nur einen Teil eines physikalischen Kanals belegen und unterteilen sich in zwei Kategorien:
- Traffic Channels (deutsch: Verkehrskanäle) werden ausschließlich für die Übertragung von Benutzerdatenströmen wie Sprache, Fax und Daten genutzt. Diese Kanäle sind für beide Richtungen – also
- Mobile Station (MS) ⇔ Base Station Subsystem (BSS)
- ausgelegt und können entweder durch einen Vollraten–Verkehrskanal $\text{(13 kbit/s)}$ oder von zwei Halbratenkanälen $\text{(je 5.6 kbit/s)}$ belegt werden.
- Control Channels (deutsch: Signalisierungskanäle) versorgen über die Funkschnittstelle alle aktiven Mobilstationen durch eine paketorientierte Signalisierung, um jederzeit Nachrichten von der Base Transceiver Station (BTS ) empfangen bzw. Nachrichten an die BTS senden zu können.
Die Tabelle listet die logischen Kanäle des GSM auf.
- Diese unterscheiden sich von den logischen ISDN–Kanälen durch ein zusätzliches „m” für „mobile”.
- Beispielsweise ist der „Bm–Kanal” vergleichbar mit dem B–Kanal des ISDN.
Uplink– und Downlink–Parameter
Die logischen Kanäle werden auf physikalische Kanäle abgebildet, die alle physikalischen Aspekte des Datentransportes beschreiben:
- die Frequenzbereiche für Uplink (Funkstrecke Mobilstation → Basisstation) und Downlink (Funkstrecke Basisstation → Mobilstation),
- die Aufteilung zwischen Time Division Multiple Access (TDMA) und Frequency Division Multiple Access (FDMA),
- die Burststruktur, also die Belegung eines TDMA-Zeitschlitzes bei verschiedenen Anwendungen (Benutzer- und Signalisierungsdaten, Synchronisationsmarken, usw.),
- das Modulationsverfahren Gaussian Minimum Shift Keying (GMSK), eine Variante von Continuous Phase – Frequency Shift Keying (CP–FSK) mit großer Bandbreiteneffizienz.
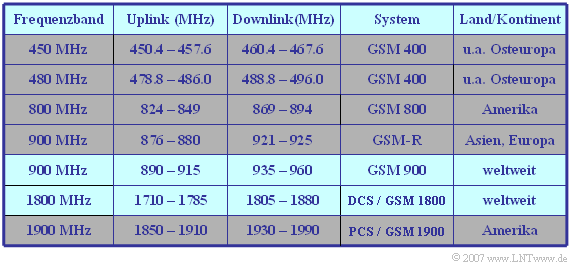
Die folgende Tabelle zeigt die Frequenzbereiche der standardisierten GSM–Systeme. Damit zwischen den beiden Richtungen keine Intermodulationsstörungen auftreten, liegt zwischen den Bändern für Uplink und Downlink ein Sicherheitsband, der so genannte Duplexabstand.
$\text{Beispiel 1:}$ Beim $\text{System GSM 900}$ (in Deutschland: D–Netz) beginnt der Uplink bei $\text{890 MHz}$ und der Downlink bei $\text{935 MHz}$.
- Der Duplexabstand beträgt somit $\text{45 MHz}$.
- Sowohl der Uplink als auch der Downlink besitzen eine Bandbreite von $\text{25 MHz}$.
- Abzüglich der Guard–Bänder an den beiden Rändern von jeweils $\text{100 kHz}$ verbleiben $\text{24.8 MHz}$, die in $124$ FDMA-Kanäle zu je $\text{200 kHz}$ unterteilt sind.
Das $\text{DCS–Band}$ (E–Netz) im Bereich um $\text{1800 MHz}$ hat einen Duplexabstand von $\text{95 MHz}$ und eine jeweilige Bandbreite von $\text{75 MHz}$.
- Unter Berücksichtigung der Guard–Bänder ergeben sich hier $374$ FDMA–Kanäle zu je $\text{200 kHz}$.
Realisierung von FDMA und TDMA
Beim GSM–System werden zwei Vielfachzugriffsverfahren parallel verwendet:
- Frequenzmultiplex (Frequency Division Multiple Access, FDMA) und
- Zeitmultiplex (Time Division Multiple Access, TDMA).
Die Grafik und die Beschreibung gilt für das System $\text{GSM 900}$, in Deutschland bekannt als D–Netz.
Bei den anderen GSM–Systemen gelten vergleichbare Aussagen.
Wir verweisen hier auch auf die Seite GSM–Rahmenstruktur und die Aufgabe 3.3.
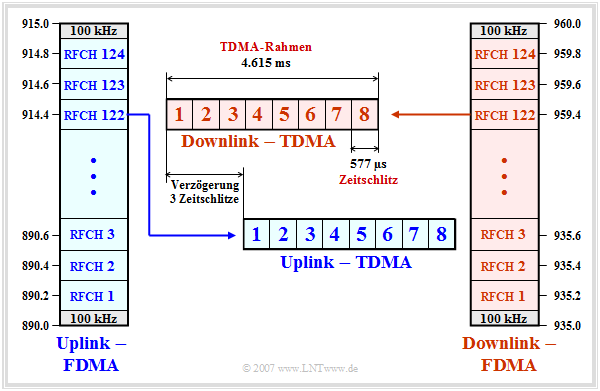
- Sowohl im Uplink als auch im Downlink geschieht die Übertragung der Signalisierungs– und Verkehrsdaten parallel in $124$ Frequenzkanälen, bezeichnet mit „RFCH1” bis „RFCH124”.
- Die Mittenfrequenz des Uplink–Kanals $n$ liegt bei $890 \ {\rm MHz} + n · 0.2 \ {\rm MHz} \ \ ( n = 1$, ... , $124)$. Am oberen und unteren Ende des $25 \ {\rm MHz}$–Bandes gibt es Schutzbereiche von je $100 \ {\rm kHz}$.
- Der Kanal $n$ im Downlink liegt um den Duplexabstand von $45 \ {\rm MHz}$ über dem Kanal $n$ im Uplink bei $935 \ {\rm MHz} + n · 0.2 \ {\rm MHz}$. Die Kanäle werden ebenso bezeichnet wie diejenigen in der Aufwärtsstrecke.
- Jeder Zelle werden einige Frequenzen per Cell Allocation (CA) zugewiesen. In benachbarten Zellen verwendet man verschiedene Frequenzen. Eine Teilmenge der CA ist für logische Kanäle reserviert. Die verbleibenden Kanäle werden einer Mobilstation als Mobile Allocation (MA) zugewiesen.
- Diese wendet man zum Beispiel bei Frequenzsprungverfahren (Frequency Hopping) an, wobei die Daten über verschiedene Frequenzkanäle gesendet werden. Die Übertragung wird dadurch stabiler gegenüber Kanalschwankungen. Meist erfolgt der Frequenzwechsel paketweise.
- Die einzelnen GSM–Frequenzkanäle werden durch Zeitmultiplex (TDMA) noch weiter unterteilt. Jeder FDMA–Kanal wird periodisch in so genannte TDMA–Rahmen aufgeteilt, die ihrerseits jeweils acht Zeitschlitze (Time–Slots) umfassen.
- Die Zeitschlitze (TDMA–Kanäle) werden zyklisch den einzelnen Teilnehmern zugeordnet und beinhalten jeweils einen so genannten Burst von $156.25$ Bitperioden Länge. Jedem GSM-Nutzer steht in jedem TDMA–Rahmen genau einer der acht Zeitschlitze zur Verfügung.
- Die TDMA–Rahmen des Uplinks werden gegenüber denen des Downlinks mit drei Zeitschlitzen Verzögerung gesendet. Dies hat den Vorteil, dass die gleiche Hardware einer Mobilstation sowohl zum Senden als auch zum Empfangen einer Nachricht eingesetzt werden kann.
- Die Dauer eines Zeitschlitzes beträgt $T_{\rm Z} ≈ 577 \ \rm µ s$, die eines TDMA–Rahmens $4.615 \ \rm ms$. Diese Werte ergeben sich aus der GSM–Rahmenstruktur. Insgesamt $26$ TDMA–Rahmen werden zu einem so genannten Multiframe der Dauer $120 \ \rm ms$ zusammengefasst:
- $$T_{\rm Z} = \frac{120\,{\rm ms}}{8 \cdot 26} \approx 576.9\,{\rm µ s }\hspace{0.05cm}. $$
Die verschiedenen Burstarten bei GSM
Wie gerade gezeigt wurde, beinhaltet ein Burst jeweils $156.25$ Bit und hat die Dauer $T_{\rm Z} ≈ 577 \ \rm µ s$.
- Daraus berechnet sich die Bitdauer zu $T_{\rm B} ≈ 3.69 \ \rm µ s$.
- Zur Vermeidung von Überlappungen von Bursts aufgrund unterschiedlicher Laufzeiten zwischen Mobil– und Basisstation ist am Ende eines jeden Bursts eine Guard Period (GP) eingefügt.
- Dieser Sicherheitsabstand beträgt $8.25$ Bitdauern, also $8.25 · 3.69 \ {\rm µ s} ≈ 30.5 \ {\rm µ s}$.
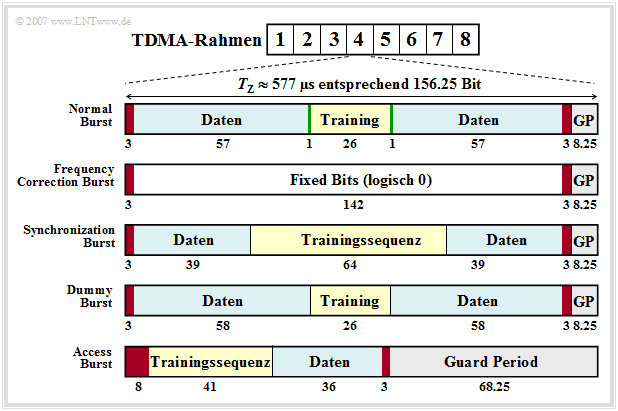
Man unterscheidet fünf verschiedene Arten von Bursts, wie aus obigem Bild hervorgeht:
- Normal Burst (NB),
- Frequency Correction Burst (FB),
- Synchronization Burst (SB),
- Dummy Burst (DB),
- Access Burst (AB).
- Der Normal Burst wird eingesetzt, um Daten von Verkehrs– und Signalisierungskanälen zu übertragen. Die fehlerschutzcodierten Nutzdaten (blau, zwei mal $57$ Bits) ergeben zusammen mit je drei Tailbits (rot, in dieser Zeit wird die Sendeleistung geregelt), zwei Signalisierungsbits (grün) und $26$ Bits für die Trainingssequenz (gelb, erforderlich für die Kanalschätzung und Synchronisation) insgesamt $148$ Bit. Dazu kommt die Guard Period von $8.25$ Bit (grau).
- Die zwei (grünen) Signalisierungsbits – auch Stealing Flags genannt – zeigen an, ob der Burst lediglich Nutzdaten oder hochpriorisierte Signalisierungsinformationen transportiert, die immer verzögerungsfrei zu übertragen sind. Mit Hilfe der Trainingssequenz kann der Kanal geschätzt werden, was eine Voraussetzung für die Anwendung eines Entzerrers zur Verminderung von Impulsinterferenzen ist.
- Der Frequency Correction Burst wird zur Frequenzsynchronisierung einer Mobilstation verwendet. Alle Bits außer den Tailbits und der Guard Period sind hier auf logisch „$0$” gesetzt. Die wiederholte Ausstrahlung eines solchen Bursts auf dem Frequency Correction Channel (FCCH) entspricht einem unmodulierten Trägersignal mit der Frequenz $f_{\rm T} + Δf_{\rm A}$ (Trägerfrequenz + Frequenzhub). Dieser Wert ergibt sich aus der Tatsache, dass das Modulationsverfahren Gaussian Minimum Shift Keying ein FSK–Sonderfall ist.
- Mit dem Synchronization Burst werden Informationen übertragen, mit deren Hilfe sich eine Mobilstation zeitlich mit der BTS synchronisiert. Neben einer langen Midambel von $64$ Bit enthält der Synchronization Burst die TDMA–Rahmen–Nummer und den Base Transceiver Station Identity Code (BSIC). Bei wiederholter Ausstrahlung eines solchen Bursts spricht man vom Synchronization Channel (SCH).
- Der Dummy Burst (DB) wird von jeder Base Transceiver Station (BTS) auf einer speziell ihr zugeteilten Frequenz (Cell Allocation) ausgesandt, wenn keine anderen Bursts zu versenden sind. Damit ist sichergestellt, dass eine Mobilstation stets Leistungsmessungen durchführen kann.
- Der Access Burst wird für wahlfreien Vielfachzugriff auf dem Random Access Channel (RACH) eingesetzt. Um die Wahrscheinlichkeit von Kollisionen auf dem RACH gering zu halten, besitzt der Access Burst eine wesentliche längere Guard Period von $68.25$ Bitdauern als die übrigen Bursts.
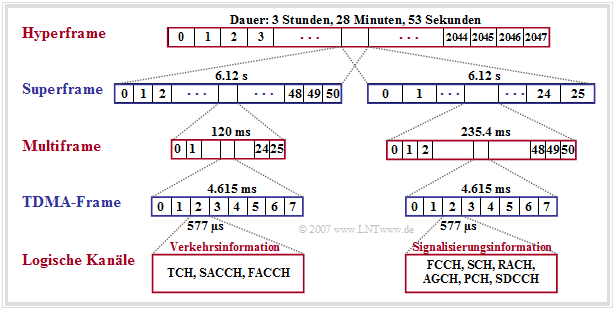
GSM–Rahmenstruktur
Durch die GSM–Rahmenstruktur erfolgt die Abbildung der logischen Kanäle auf physikalische Kanäle. Hierbei wird unterschieden zwischen
- der Abbildung in der Frequenz, basierend auf Cell Allocation (CA), Mobile Allocation (MA), der TDMA–Rahmennummer (FN) und den Vorschriften für das (optionale) Frequency Hopping,
- der Abbildung in der Zeit, wobei die TDMA–Rahmen mit jeweils acht Zeitschlitzen zur Übertragung der Bursts in Multiframes, Superframes und Hyperframes zusammengefasst werden.
Entsprechend diesem Bild gelten folgende Aussagen:
- Multiframes werden für die Abbildung von logischen Kanälen auf physikalische Kanäle genutzt. Hierbei sind zwei Arten zu unterscheiden, solche mit $26$ TDMA–Rahmen und einer Zyklusdauer von $120 \ \rm ms$ und solche mit $51$ TDMA–Rahmen und einer Dauer von $235.4 \ \rm ms$.
- Die Bursts der Verkehrskanäle (TCH) und der zugeordneten Steuerungskanäle (SACCH, FACCH) werden in jeweils $26$ aufeinander folgenden TDMA-Rahmen übertragen. Dabei wird stets nur ein Zeitschlitz je TDMA-Rahmen für den jeweiligen Multiframe berücksichtigt.
- Von der Brutto–Datenrate pro Nutzer $\text{(ca. 33.9 kbit/s)}$ sind $\text{9.2 kbit/s}$ für Synchronisierung, Signalisierung und Guard Period reserviert und $\text{1.9 kbit/s}$ für SACCH und IDLE. Die (codierten und verschlüsselten) Nutzdaten belegen bei Multiframe-Struktur mit $26$ Rahmen nur $\text{22.8 kbit/s}$.
- Die Multiframe-Struktur mit $51$ Rahmen (rechte Bildhälfte) dient dazu, mehrere logische Kanäle auf einen physikalischen Kanal zu multiplexen. In 51 aufeinander folgenden TDMA–Rahmen werden jeweils alle Daten der Signalisierungskanäle (außer FACCH und SACCH) übertragen.
- Ein Superframe besteht aus $1326$ aufeinander folgenden TDMA-Rahmen $(51$ Multiframes mit je $26$ TDMA–Rahmen bzw. aus $26$ Multiframes mit je $51$ TDMA–Rahmen$)$ und dauert ca. $6.12$ Sekunden.
- Ein Hyperframe fasst jeweils $2048$ Superframes (bzw. $2\hspace{0.08cm}715{\hspace0.08cm}648$ TDMA–Rahmen) zusammen und wird mit seiner langen Zyklusdauerzur Synchronisierung der Nutzdatenverschlüsselung verwendet. Diese beträgt $\text{3 Stunden, 28 Minuten und 53.760 Sekunden}.$
Modulation bei GSM–Systemen
Entsprechend den Aussagen der letzten Seiten müssen in einem Frequenzkanal $156.25$ Bit pro Zeitschlitz $(0.5769 \ \rm ms)$ übertragen werden. Dies entspricht einer Gesamtbitrate (für acht TDMA–Nutzer inkl. Kanalcodierung, Signalisierungs– und Synchronisationsinformation, etc.) von $R_{\rm ges} = 270\hspace{0.08cm}833 \ \rm bit/s$.
Für diese Bitrate steht bei GSM eine Bandbreite von $B = 200 \ \rm kHz$ zur Verfügung. Man benötigt deshalb ein Modulationsverfahren mit einer Bandbreiteneffizienz von mindestens $β =R_{\rm ges}/B = 1.35$.
Beim GSM–Mobilfunk findet das Modulationsverfahren Gaussian Minimum Shift Keying (GMSK) Anwendung. Dieses wurde schon im Kapitel Nichtlineare digitale Modulation des Buches „Modulationsverfahren” ausführlich behandelt. Hier folgt eine kurze, stichpunktartige Beschreibung:
- GMSK ist eine abgewandelte Form von Frequency Shift Keying (FSK). Diese ergibt sich, wenn man einen Frequenzmodulator mit einem binären bipolaren rechteckförmigen Eingangssignal betreibt.
- Ein solches FSK-Signal $s(t)$ beinhaltet innerhalb einer jeden Symboldauer $T$ jeweils nur eine einzige Augenblicksfrequenz $f_{\rm A}(t) = \rm const.$ Ist das (normierte) Eingangssignal gleich $+1$, so ist $f_{\rm A}(t)$ gleich der Summe aus der Trägerfrequenz $f_{\rm T}$ und dem Frequenzhub $Δf_{\rm A}$. Entsprechend gilt für den Amplitudenwert $-1$: $f_{\rm A}(t) = f_{\rm T} - Δf_{\rm A}$.
- Um eine einfache Demodulation zu ermöglichen, sollten die beiden Signale mit den Frequenzen $f_{\rm T} ± Δf$ innerhalb der Symboldauer $T$ orthogonal zueinander sein. Demzufolge muss gelten:
- $$\int^{T} _{0} \cos \big(2 \pi t \cdot (f_{\rm T}+ \Delta f_{\rm A} )\big)\cdot \cos \big(2 \pi t \cdot (f_{\rm T}- \Delta f_{\rm A} )\big)\,{\rm d}t= 0\hspace{0.05cm}. $$
- Daraus ergibt sich für den Frequenzhub die Anforderung:
- $$\Delta f_{\rm A} = \frac{k}{4 \cdot T}\hspace{0.2cm}{\rm mit}\hspace{0.2cm}k = 1, 2, 3, \text{...}$$
- Da bei FSK–Systemen der Modulationsindex zu $h = 2 · Δf_{\rm A} · T$ definiert ist, folgt $h = k/2$. Der kleinste Wert unter Einhaltung der Orthogonalitätsbedingungen ist somit $h_{\rm min} = 0.5$.
- Ein FSK–System mit $h = 0.5$ bzw. $Δf_{\rm A}$ = ${1}/{4T}$ bezeichnet man als Minimum Shift Keying – kurz MSK. Dieses wird in allen GSM-Systemen eingesetzt, da ein größerer Modulationindex als $h = 0.5$ eine deutlich größere Bandbreite beanspruchen würde.
- Ein sehr schmales Spektrum ergibt sich allerdings nur dann, wenn an den Symbolgrenzen Phasensprünge durch Phasenwertanpassung vermieden werden. MSK gehört somit zu den Continuous Phase Frequency Shift Keying–Verfahren (CP–FSK, siehe nächste Seite).
- Vor dem Frequenzmodulator wird zusätzlich noch ein Tiefpass mit Gauß–Charakteristik eingefügt, wodurch die GSM–Bandbreite weiter verringert wird. Man nennt diese Modulationsart Gaussian Minimum Shift Keying (GMSK).
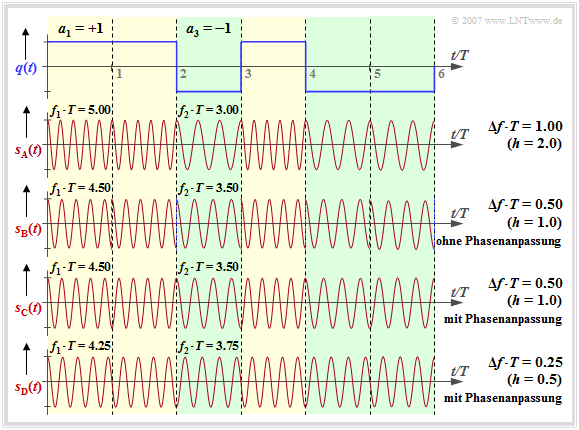
Kontinuierliche Phasenanpassung bei FSK
Ausgehend vom Rechtecksignal $q(t)$ und der Trägerfrequenz $f_{\rm T} = 4/T$ betrachten wir die FSK–Signale $s_{\rm A}(t)$, ... , $s_{\rm D}(t)$ bei unterschiedlichem Frequenzhub $Δf_{\rm A}$ ⇒ Modulationindex $h = 2 · Δf_{\rm A} · T$.
Zu den Signalverläufen ist anzumerken (wir verweisen auch auf das interaktive Applet Frequency Shift Keying & Continuous Phase Modulation):
- Das Signal $s_{\rm A}(t)$ ergibt sich mit $Δf_{\rm A} = 1/T$ ⇒ Modulationsindex $h = 2$. Man erkennt die höhere Frequenz $f_1 = 5/T$ $($für $a_ν = +1)$ gegenüber der Frequenz $f_2 = 3/T$ $($für $a_ν = -1)$.
- Mit $Δf_{\rm A} = 0.5/T$ $($Signal $s_{\rm {\rm B}}(t)$, $h = 1)$ gilt $f_1 = 4.5/T$ und $f_2 = 3.5/T$. An jeder Symbolgrenze tritt ein Phasensprung um $π$ auf, wenn keine Phasenanpassung wie beim Signal $s_{\rm C}(t)$ vorgenommen wird.
- Bei $s_{\rm C}(t)$ wird im Bereich $0$ ... $T$ der Koeffizient $a_1 = +1$ durch $\cos(2π·f_1·t)$ repräsentiert, während der ebenfalls positive Koeffizient $a_2 = +1$ im Bereich $T$ ... $2T$ zum Signal $-\cos(2π·f_1\hspace{0.01cm}·\hspace{0.01cm}(t-T))$ führt. Durch diese Anpassung werden somit Phasensprünge vermieden.
- Das Signal $s_{\rm D}(t)$ beschreibt das MSK-Signal $($Frequenzhub $Δf_{\rm A} = 0.25/T$ ⇒ Modulationsindex $h = 0.5)$, ebenfalls mit Phasenanpassung. Hier sind bei jeder Symbolgrenze – je nach den vorherigen Symbolen – vier unterschiedliche Anfangsphasen möglich.
- Bei $\rm GSM \ 900$ beträgt die Trägerfrequenz $f_{\rm T} = 900\ \rm MHz$ und die Symboldauer ist $T ≈ 3.7 \ \rm µ s$. Mit dem Modulationsindex $h = 0.5$ ergibt sich $Δf_{\rm A} ≈ 68 \ \rm kHz$. Die beiden Frequenzen $f_1 = 900.068\ \rm MHz$ und $f_2 = 899.932 \ \rm MHz$ liegen somit sehr eng beieinander.
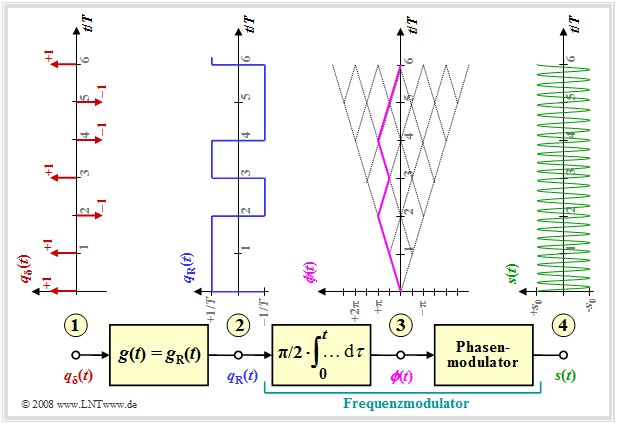
Minimum Shift Keying (MSK)
Die Grafik zeigt das Modell zur Erzeugung einer MSK–Modulation und typische Signalverläufe. Man erkennt
- am Punkt 1 das digitale Quellensignal, bestehend aus einer Folge von Diracimpulsen im Abstand $T$, gewichtet mit den Amplitudenkoeffizienten $a_ν ∈ \{-1, +1\}$:
- $$q_\delta(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot \delta (t - \nu \cdot T)\hspace{0.05cm}, $$
- am Punkt 2 das Rechtecksignal $q_{\rm R}(t)$ nach Faltung mit dem Rechteckimpuls $g(t)$ der Dauer $T$ und der Höhe $1/T$ (die Amplitude wurde aus Kompatibilitätsgründen zu späteren Seiten so gewählt):
- $$q_{\rm R}(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g (t - \nu \cdot T)\hspace{0.05cm}, $$
- den Frequenzmodulator, der sich gemäß dem Kapitel Signalverläufe bei FM als Integrator und nachgeschalteten Phasenmodulator realisieren lässt. Für das Signal am Punkt 3 gilt dann:
- $$\phi(t) = \frac{\pi}{2}\cdot \int_{0}^{t} q_{\rm R}(\tau)\hspace{0.1cm} {\rm d}\tau \hspace{0.05cm}.$$
Die Phasenwerte bei der Symboldauer $T$ sind Vielfache von $π/2 \ (90^\circ)$, wobei der für MSK gültige Modulationsindex $h = 0.5$ berücksichtigt ist. Der Phasenverlauf ist linear. Daraus ergibt sich am Punkt 4 des Blockschaltbildes das MSK–Signal zu
- $$s(t) = s_0 \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm}t + \phi(t)) = s_0 \cdot \cos (2 \pi \cdot t \cdot (f_{\rm T}+a_{ \nu} \cdot {\rm \Delta}f_{\rm A} )) \hspace{0.05cm}.$$
Die Realisierung von Minimum Shift Keying (MSK) durch eine spezielle Variante von Offset–QPSK wird durch das interaktive Applet QPSK und Offset–QPSK verdeutlicht:
Gaussian Minimum Shift Keying (GMSK)
Ein Vorteil von MSK gegenüber anderen Modulationsarten ist der geringere Bandbreitenbedarf. Durch geringfügige Modifikationen hin zum [[Modulationsverfahren/Nichtlineare_digitale_Modulation#GMSK_.E2.80.93_Gaussian_Minimum_Shift_Keying|Gaussian Minimum Shift Keying – abgekürzt GMSK– ergibt sich nochmals eine schmaleres Spektrum.
Man erkennt aus dem Blockschaltbild folgende Unterschiede zum MSK (wir verweisen wieder auf das interaktive Applet Frequency Shift Keying & Continuous Phase Modulation):
- Der Frequenzimpuls g(t) ist nun nicht mehr rechteckförmig wie der Impuls $g_{\rm R}(t)$, sondern weist flachere Flanken auf. Demzufolge ergibt sich auch ein weicherer Phasenverlauf (Punkt 3) als beim MSK–Verfahren (siehe letzte Seite), bei dem $ϕ(t)$ symbolweise linear ansteigt bzw. abfällt.
- Man erreicht diese sanfteren Phasenübergänge bei GMSK durch ein Gaußtiefpassfilter mit dem Frequenzgang bzw. der Impulsantwort
- $$H_{\rm G}(f) = {\rm e}^{-\pi\cdot (\frac{f}{2 \cdot f_{\rm G}})^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\cdot (2 \cdot f_{\rm G}\cdot t)^2}\hspace{0.05cm}.$$
- Bei GSM ist die 3dB–Grenzfrequenz zu $f_{\rm 3dB} = 0.3/T$ festgelegt. Wie in Aufgabe A3.4 gezeigt wird, gilt somit für die systemtheoretische Grenzfrequenz $f_{\rm G} ≈ 1.5 · f_{\rm 3dB} = 0.45/T$.
- Der resultierende Frequenzimpuls $g(t)$ am Punkt 2 des Blockschaltbildes ergibt sich aus der Faltung des Recheckimpulses $g_{\rm R}(t)$ mit der Impulsantwort $h_{\rm G}(t)$ des Gaußtiefpasses zu
- $$g(t) = g_{\rm R}(t) \star h_{\rm G}(t)\hspace{0.05cm}. $$
- Das GMSK–modulierte Signal $s(t)$ weist nun nicht mehr abschnittsweise (je Symboldauer) eine konstante Frequenz auf. Diesen Unterschied zur MSK kann man allerdings aus dem Signalverlauf am Punkt 4 des Blockschaltbildes nur schwer erkennen.
Vor– und Nachteile von GMSK
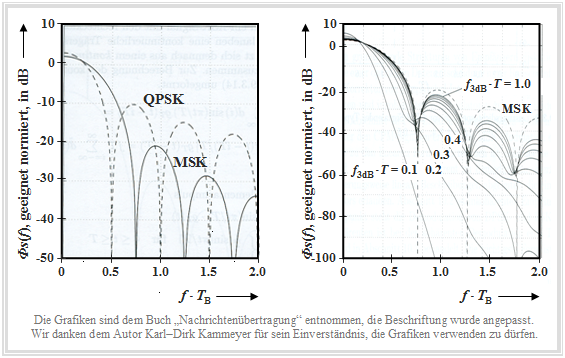
Hier werden die wichtigsten Merkmale des Modulationsverfahren Gaussian Minimum Shift Keying zusammenfassend aufgeführt. Ein wesentlicher Vorteil von GMSK ist der sehr geringe Bandbreitenbedarf. Die linke Grafik zeigt das logarithmierte Leistungsdichtespektrum $10 · \text{lg} ß {\it Φ}_s(f)/{\it Φ}_0$ des Verfahrens Minimum Shift Keying (MSK) im Vergleich zu Quaternary Phase Shift Keying (QPSK), wobei ${\it Φ}_0$ „geeignet” gewählt wurde.
Man erkennt aus dieser dem Buch [Kam04][1] entnommenen Darstellung. Auf der Abszisse ist die normierte Frequenz $f · T_{\rm B}$ aufgetragen. Bei MSK ist die Bitdauer $T_{\rm B}$ gleich der Symboldauer $T$, während bei QPSK $T_{\rm B} = T/2$ gilt. Im rechten Diagramm, das sich ausschließlich auf (G)MSK bezieht, könnte die Abszisse auch mit $f · T$ beschriftet werden.
- Betrachten wir zunächst die linke Grafik: Die erste Nullstelle im Leistungsdichtespektrum (LDS) tritt bei der QPSK (gestrichelte Kurve) beim normierten Abszissenwert $f · T_{\rm B} = 0.5$ auf, bei der MSK dagegen erst bei $f · T_{\rm B} = 0.75$.
- Im weiteren Verlauf ergibt sich jedoch bei MSK ein deutlich schnellerer LDS–Abfall als der asymptotische $f^{-2}$–Abfall bei QPSK. Zu beachten ist, dass für die MSK ein Cosinusimpuls zur Spektralformung zugrunde liegt und für die QPSK ein Rechteckimpuls.
Die rechte Darstellung zeigt den Einfluss der gaußförmigen Impulsformung bei GMSK auf das Leistungsdichtespektrum ${\it Φ}_s(f)$, wobei als Parameter die normierte 3dB–Grenzfrequenz verwendet wird.
- Je kleiner $f_{\rm 3\ dB}$ ist, desto schmalbandiger ist das Leistungsdichtespektrum. Im GSM–Standard wurde $f_{\rm 3\ dB} · T$ = 0.3 festgelegt. Mit diesem Wert wird die Bandbreite bereits entscheidend reduziert, was zu geringeren Nachbarkanalinterferenzen führt.
- Andererseits wirken sich mit dieser Grenzfrequenz die Impulsinterferenzen schon gravierend aus. Die Augenöffnung ist kleiner als $50\%$ und es ist eine geeignete Entzerrung vorzusehen.
Des Weiteren ist zu vermerken:
- Die binäre FSK stellt – auch bei kontinuierlicher Phasenanpassung – allgemein ein nichtlineares Modulationsverfahren dar. Deshalb ist eine kohärente Demodulation eigentlich nicht möglich.
- Eine Ausnahme bildet die MSK als Sonderfall für den Modulationsindex $h = 0.5$, die sich als Offset–QPSK linear realisieren lässt und somit auch kohärent demoduliert werden kann.
- Ohne Berücksichtigung der Impulsinterferenzen beträgt die Bitfehlerwahrscheinlichkeit
- $$p_{\rm B} = {\rm Q} \left(\sqrt{{E_{\rm B}}/{N_0}}\hspace{0.09cm}\right) = {1}/{2}\cdot{\rm erfc} \left(\sqrt{{E_{\rm B}}/{2N_0}}\hspace{0.09cm}\right) \hspace{0.05cm}.$$
- Gegenüber der QPSK ergibt sich eine Degradation um $3\ \rm dB$. Das interaktive Applet Komplementäre Gaußsche Fehlerfunktionen liefert die Zahlenwerte der hier verwendeten Funktionen ${\rm Q}(x)$ bzw. $1/2 \cdot {\rm erfc}(x)$.
- Ein Vorteil der GMSK gegenüber der QPSK ist, dass sich trotz der spektralen Formung des Grundimpulses eine konstante Hüllkurve ergibt. Deshalb spielen Nichtlinearitäten auf dem Kanal nicht eine so große Rolle als bei anderen Modulationsverfahren. Dies ermöglicht den Einsatz einfacher und kostengünstiger Leistungsverstärker, einen geringeren Leistungsverbrauch und damit auch längere Betriebsdauern akkubetriebener Geräte.
Radio Subsystem Link Control
Eine weitere Funktion der Funkschnittstelle ist die Steuerung der Funkverbindung. So übernimmt das so genannte Radio Subsystem Link Control folgende Aufgaben:
Es ist für die Messung der Empfangsqualität zuständig. Während einer aufgebauten Verkehrs– oder Signalisierungsverbindung erfolgt in regelmäßigen Abständen die Kanalvermessung der Mobilstation hinsichtlich Empfangsfeldstärke und Bitfehlerrate ⇒ Quality Monitoring. Diese Werte werden in einem Messreport zur Basisstation über den Signalisierungskanal SACCH übertragen und von dieser für die Leistungsregelung und das Handover verwendet.
Die Power Control (deutsch: Leistungsregelung) ist erforderlich, damit alle Mobilstationen nur mit der minimal erforderlichen Energie abstrahlen. Die Sendeleistung kann adaptiv in Schritten von $2 \ \rm dBm$ zwischen $43 \ \rm dBm$ (Stufe $0$: $20\ \rm W$) und $13 \ \rm dBm$ (Stufe $15$: $20\ \rm mW$) geregelt werden. Auch die Sendeleistung der Basisstationen wird in Schritten von $2 \ \rm dBm$, um optimale Netzkapazität zu erzielen. Eine Ausnahme bildet der BCCH–Träger mit konstanter Sendeleistung, um den Mobilstationen eine vergleichende Messung benachbarter BCCH–Träger zu ermöglichen.
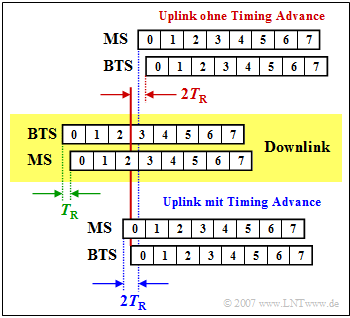
Das Adaptive Frame Alignment – also die adaptive Rahmensynchronisation – dient dazu, Kollisionen zwischen Uplink– und Downlinkdaten zu vermeiden, die von der Mobilstation um drei Zeitschlitze versetzt gesendet bzw. empfangen werden sollen. Dies zeigt nebenstehende Grafik.
Im mittleren, gelb hinterlegten Bereich ist der Downlink dargestellt, wobei die Daten um die Zeit $T_{\rm R}$ (Round Trip Delay Time) später bei der Mobilstation (MS) ankommen, als sie von der Base Transceiver Station (BTS) gesendet wurden (grüne Markierung).
Im oberen Bereich ist der Uplink ohne Timing Advance dargestellt.
- Die MS beginnt genau drei Zeitschlitze nach dem Empfang mit dem Senden (blaue Markierung).
- Aufgrund der Verzögerungen im Downlink und Uplink erreicht der Zeitschlitz $0$ die BTS nicht wie gefordert zu der Zeit $3T_{\rm Z}$, sondern um $2T_{\rm Z}$ später (rote Markierung).
- Beim Timing Advance Uplink (untere Skizze) wird diese Verzögerung bereits von der Mobilstation kompensiert, indem die Daten um die Zeit $T_{\rm A} = 2T_{\rm R}$ früher versandt werden und diese somit genau zeitsynchron bei der BTS ankommen.
Für das Timing Advance stehen $64$ Stufen $(0 – 63)$ zur Verfügung, wobei jede Stufe einer Bitdauer $T_{\rm B}$ entspricht.
Das maximale Timing Advance beträgt somit $\rm 63 · 3.7 \ µ s ≈ 233 \ µs$, so dass sich die maximale zulässige Laufzeit in einer Richtung zu $T_{\rm R} ≈ 116\ {\rm µ s}$ ergibt. Daraus ergibt sich der erlaubte Zellenradius von GSM (Entfernung zwischen BTS und MS) zu $116\ \rm µ s · 3 · 10^8 \ m/s ≈ 35 \ km$.
Aufgaben zum Kapitel
Aufgabe 3.3: GSM–Rahmenstruktur
Aufgabe 3.3Z: GSM 900 und GSM 1800
Aufgabe 3.4Z: FSK mit kontinuierlicher Phase
Quellenverzeichnis
- ↑ Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.