Aufgaben:Exercise 2.5: Residual Redundancy with LZW Coding

• Return to book

Restredundanz  $r(N)$  & Näherung  $r\hspace{0.05cm}'(N)$  dreier Binärquellen

Wir gehen hier von einer binären Eingangsfolge der Länge  $N$  aus und betrachten drei verschiedene binäre Nachrichtenquellen:

• $\rm BQ1$:   Symbolwahrscheinlichkeiten  $p_{\rm A} = 0.89$  und  $p_{\rm B} = 0.11$, also unterschiedlich
    ⇒   Entropie  $H = 0.5\text{ bit/Quellensymbol}$   ⇒   die Quelle ist redundant.
• $\rm BQ2$:   $p_{\rm A} = p_{\rm B} = 0.5$  (gleichwahrscheinlich)
    ⇒   Entropie  $H = 1\text{ bit/Quellensymbol}$   ⇒   die Quelle ist redundanzfrei.
• $\rm BQ3$:   Hier gibt es keine konkreten Angaben zur Statistik. 
  In der Teilaufgabe  (6)  sollen Sie die Entropie  $H$  dieser Quelle abschätzen.

Für diese drei Quellen wurden per Simulation die jeweilige Restredundanz  $r(N)$  ermittelt, die nach der  Lempel–Ziv–Welch–Codierung  in der Binärfolge verbleibt. 

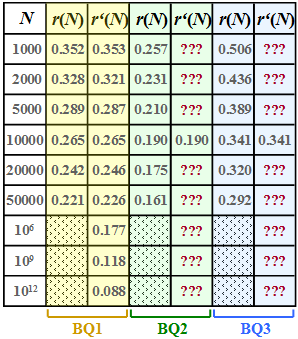
Die Ergebnisse sind in der jeweils ersten Spalte obiger Tabelle für die Quellen

• $\rm BQ1$  (gelbe Hinterlegung),
• $\rm BQ2$  (grüne Hinterlegung) und
• $\rm BQ3$  (blaue Hinterlegung)

eingetragen, wobei wir uns bei der Simulation auf Folgenlängen  $N ≤ 50000$  beschränkt haben.

Die relative Redundanz der Ausgangsfolge – vereinfachend Restredundanz genannt – kann aus

• der Länge  $N$  der Eingangsfolge,
• der Länge  $L(N)$  der Ausgangsfolge und
• der Entropie  $H$

in folgender Weise berechnet werden:

$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$

Hierbei ist berücksichtigt, dass bei perfekter Quellencodierung die Länge der Ausgangsfolge bis auf den Wert  $L_{\rm min} = N · H$  herabgesenkt werden könnte.

• Bei nichtperfekter Quellencodierung gibt  $L(n) - N · H$  die verbleibende Redundanz (mit der Pseudo–Einheit „bit”) an.
• Nach Division durch  $L(n)$  erhält man die relative Redundanz  $r(n)$  mit dem Wertebereich zwischen Null und Eins; $r(n)$ sollte möglichst klein sein.

Eine zweite Kenngröße zur Effizienzmessung der LZW–Codierung ist der  Komprimierungsfaktor  $K(N)$, der als der Quotient der Längen von Ausgangs– und Eingangsfolge ebenfalls klein sein sollte:

$$K(N) = {L(N) }/{N} \hspace{0.05cm},$$

Im  Theorieteil  wurde gezeigt, dass die Restredundanz  $r(n)$  oft durch die Funktion

$$r\hspace{0.05cm}'(N) =\frac {A}{{\rm lg}\hspace{0.1cm}(N)} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} \hspace{0.05cm}.$$

gut angenähert wird.

• Diese Näherung  $r\hspace{0.05cm}'(N)$  ist für  $\rm BQ1$  in der zweiten Spalte obiger Tabelle angegeben.
• In den Teilaufgaben  (4)  und  (5)  sollen Sie die Approximation für die Quellen  $\rm BQ2$  und  $\rm BQ3$  vornehmen.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Komprimierung nach Lempel, Ziv und Welch.
• Insbesondere wird Bezug genommen auf die Seiten

Restredrundanz als Maß für die Effizienz von Codierverfahren,

Effizienz der Lempel-Ziv-Codierung sowie

Quantitative Aussagen zur asymptotischen Optimalität.

• Die Beschreibungsgrößen  $K(N)$  und  $r(N)$  hängen deterministisch zusammen.

Fragebogen

1

Mit welchem Parameter  $A$  wurde die Näherung  $r\hspace{0.05cm}'(N)$  der Restredundanz für die Binärquelle  $\rm BQ1$  erstellt?

$A \ = \ $

2

Wie groß muss  $N = N_2$  bei  $\rm BQ1$  mindestens sein, damit die Restredundanz die Bedingung  $r(N) ≈ r\hspace{0.05cm}'(N) \le 5\%$  erfüllt?

$N_{2} \ = \ $ $\ \cdot 10^{21}$

3

Wie groß muss  $N = N_3$  bei  $\rm BQ1$  mindestens sein, damit der Komprimierungsfaktor  $K(N)= L(N)/N$  nicht größer ist als  $0.6$?

$N_{3} \ = \ $ $\ \cdot 10^{6}$

4

Bestimmen Sie nun die Redundanznäherung  $r\hspace{0.05cm}'(N)$  für die redundanzfreie Binärquelle $\rm BQ2$, insbesondere:

$r'(N = 50000)\ = \ $

$r'(N = 10^6)\ = \ $

$r'(N = 10^{12})\ = \ $

5

Welche Werte liefert die Redundanznäherung  $r\hspace{0.05cm}'(N)$  für die nicht näher spezifizierte Binärquelle  $\rm BQ3$? Insbesondere:

$r'(N = 50000)\ = \ $

$r'(N = 10^6)\ = \ $

$r'(N = 10^{12})\ = \ $

6

Welche Quellenentropie  $H$  könnte  $\rm BQ3$  nach diesem Ergebnis besitzen?  Hinweis: Es ist genau eine Antwort richtig.

	$H = 1.00 \ \rm bit/Quellensymbol$,
	$H = 0.75 \ \rm bit/Quellensymbol$,
	$H = 0.50 \ \rm bit/Quellensymbol$,
	$H = 0.25 \ \rm bit/Quellensymbol$.

Musterlösung

Solution

(1)  Die Näherung  $r\hspace{0.05cm}'(N)$  stimmt per Definition für die Folgenlänge  $N = 10000$  mit der per Simulation ermittelten Restredundanz  $r(N) = 0.265$  exakt überein.

• Damit ist

$$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} \hspace{0.05cm}. $$

(2)  Aus der Beziehung  ${A}/{\rm lg}\hspace{0.1cm}(N) ≤ 0.05$    ⇒    ${A}/{\rm lg}\hspace{0.1cm}(N) = 0.05$  folgt:

$${{\rm lg}\hspace{0.1cm}N_{\rm 2}} = \frac{A}{0.05} = 21.2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} N_{\rm 2} = 10^{21.2} \hspace{0.15cm}\underline{= 1.58 \cdot 10^{21}} \hspace{0.05cm}.$$

(3)  Allgemein gilt  $r(N) = 1 - {H}/{K(N)} \hspace{0.05cm}.$ 

• $\rm BQ1$  hat die Entropie  $H = 0.5$ bit/Symbol. 
• Daraus folgt wegen  $r(N) ≈ r\hspace{0.05cm}'(N)$  für  $K(N_3) = 0.6$:

$$r(N_{\rm c}) = 1 - \frac{0.5}{0.6} = 0.167 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} {\rm lg}\hspace{0.1cm}N_{\rm 3} = \frac{A}{0.167} = 6.36 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_{\rm 3} = 10^{6.36} \hspace{0.15cm}\underline{= 2.29 \cdot 10^{6}} \hspace{0.05cm}.$$

Ergebnisse für  $\rm BQ2$

(4)  Für  $N = 10000$  gilt  $r(N) ≈ r\hspace{0.05cm}'(N) = 0.19$:

$$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$

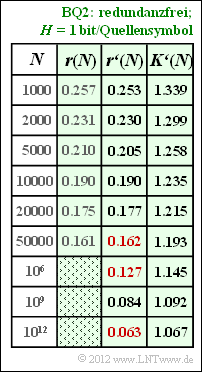
• Die Ergebnisse sind in nebenstehender Tabelle zusammengefasst.
• Man erkennt die sehr gute Übereinstimmung zwischen   $r(N)$  und  $r\hspace{0.05cm}'(N)$.
• Die gesuchten Zahlenwerte sind in der Tabelle rot markiert:

$$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.162},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.127},\hspace{0.3cm} r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.063}.$$

• Für den Komprimierungsfaktor gilt (der Apostroph weist darauf hin, dass von der Näherung  $r\hspace{0.05cm}'(N)$  ausgegangen wurde):

$$K\hspace{0.05cm}'(N) = \frac{1}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$

• Damit gilt für die Länge des LZW–Ausgabestrings:

$$L\hspace{0.05cm}'(N) = K\hspace{0.05cm}'(N) \cdot N = \frac{N}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$

Ergebnisse für  $\rm BQ3$

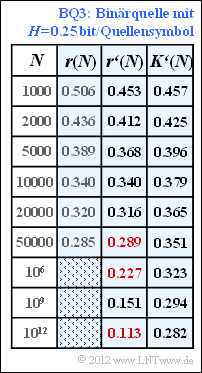
(5)  Nach ähnlicher Vorgehensweise wie in der Teilaufgabe  (4)  erhält man für die Binärquelle  $\rm BQ3$  den Anpassungsparameter  $A = 1.36$  und daraus die Ergebnisse gemäß der blau hinterlegten Tabelle.

Hinweis:   Die letzte Spalte dieser Tabelle ist nur bei Kenntnis der Teilaufgabe  (6)  verständlich. Dort wird gezeigt, dass die Quelle  $\rm BQ3$  die Entropie  $H = 0.25$ bit/Quellensymbol besitzt.

• In diesem Fall gilt für den Komprimierungsfaktor:

$$K\hspace{0.05cm}'(N) = \frac{H}{1 - r\hspace{0.05cm}'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$

• Damit erhält man für die gesuchten Werte der Restredundanz:

$$r\hspace{0.05cm}'(N = 50000)\hspace{0.15cm}\underline{ = 0.289},\hspace{0.3cm}r\hspace{0.05cm}'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.227},\hspace{0.3cm} r\hspace{0.05cm}'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.113}.$$

• Für  $N = 10^{12}$  weicht also der Komprimierungsfaktor  $(0.282)$  noch deutlich von der Entropie  $(0.25)$  ab, die erst für  $N \to \infty$  erreicht werden kann (Quellencodierungstheorem).

(6)  Die einzelnen Näherungen  $r\hspace{0.05cm}'(N)$  unterscheiden sich nur durch den Parameter  $A$.  Dabei haben wir festgestellt:

1. Quelle  $\rm BQ1$  mit  $H = 0.50$   ⇒   $A = 1.06$   ⇒   entsprechend dem Angabenblatt,
2. Quelle  $\rm BQ2$  mit  $H = 1.00$   ⇒   $A = 0.76$   ⇒   siehe Teilaufgabe  (4),
3. Quelle  $\rm BQ3$  $(H$ unbekannt$)$: $A = 4 · 0.34 =1.36$   ⇒   entsprechend der letzten Spalte in der Tabelle.

• Je kleiner die Entropie  $H$  ist, um so größer ist offensichtlich der Anpassungsfaktor  $A$  (und umgekehrt).
• Da genau eine Lösung möglich ist, muss  $H = 0.25$  bit/Quellensymbol richtig sein   ⇒   Antwort 4.

• Tatsächlich wurden bei der Simulation für die Quelle  $\rm BQ3$  die Wahrscheinlichkeiten  $p_{\rm A} = 0.96$  und  $p_{\rm B} = 0.04$    ⇒   $H ≈ 0.25$ verwendet.