Difference between revisions of "Aufgaben:Exercise 4.2: Triangular PDF"
| Line 4: | Line 4: | ||
[[File:P_ID2865__Inf_A_4_2.png|right|frame|Zweimal dreieckförmige WDF]] | [[File:P_ID2865__Inf_A_4_2.png|right|frame|Zweimal dreieckförmige WDF]] | ||
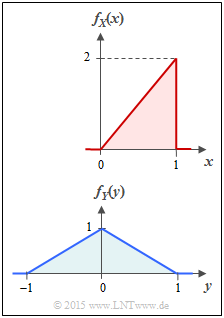
Betrachtet werden zwei Wahrscheinlichkeitsdichtefunktionen (kurz WDF) mit dreieckförmigem Verlauf. | Betrachtet werden zwei Wahrscheinlichkeitsdichtefunktionen (kurz WDF) mit dreieckförmigem Verlauf. | ||
| − | * Die Zufallsgröße $X$ ist auf den Wertebereich von $0$ | + | * Die Zufallsgröße $X$ ist auf den Wertebereich von $0$ bis $1$ begrenzt, und es gilt für die WDF (obere Skizze): |
:$$f_X(x) = \left\{ \begin{array}{c} 2x \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 1 \\ {\rm sonst} \\ \end{array} | :$$f_X(x) = \left\{ \begin{array}{c} 2x \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 1 \\ {\rm sonst} \\ \end{array} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * Die Zufallsgröße $Y$ besitzt gemäß der unteren Skizze die folgende WDF: | + | * Die Zufallsgröße $Y$ besitzt gemäß der unteren Skizze die folgende WDF: |
| − | :$$f_Y(y) = \left\{ \begin{array}{c} 1 - |y| \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |y| \le 1 \\ {\rm sonst} \\ \end{array} | + | :$$f_Y(y) = \left\{ \begin{array}{c} 1 - |\hspace{0.03cm}y\hspace{0.03cm}| \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |\hspace{0.03cm}y\hspace{0.03cm}| \le 1 \\ {\rm sonst} \\ \end{array} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| + | Für beide Zufallsgrößen soll jeweils die [[Informationstheorie/Differentielle_Entropie|differentielle Entropie]] ermittelt werden. | ||
| − | + | Beispielsweise lautet die entsprechende Gleichung für die Zufallsgröße $X$: | |
| − | |||
| − | Beispielsweise lautet die entsprechende Gleichung für die Zufallsgröße $X$: | ||
:$$h(X) = | :$$h(X) = | ||
\hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [ f_X(x) \big ] \hspace{0.1cm}{\rm d}x | \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [ f_X(x) \big ] \hspace{0.1cm}{\rm d}x | ||
\hspace{0.6cm}{\rm mit}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} | \hspace{0.6cm}{\rm mit}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Verwendet man den ''natürlichen Logarithmus'', so ist die Pseudo–Einheit „nat” anzufügen. | + | *Verwendet man den ''natürlichen Logarithmus'', so ist die Pseudo–Einheit „nat” anzufügen. |
| − | *Ist das Ergebnis dagegen in „bit” gefragt, so ist der <i>Logarithmus dualis</i> ⇒ „ | + | *Ist das Ergebnis dagegen in „bit” gefragt, so ist der <i>Logarithmus dualis</i> ⇒ „$\log_2$” zu verwenden. |
| − | In der vierten Teilaufgabe wird die neue Zufallsgröße $Z = A \cdot Y$ betrachtet. Der WDF–Parameter $A$ ist dabei so zu bestimmen, dass die differentielle Entropie der neuen Zufallsgröße $Z$ | + | In der vierten Teilaufgabe wird die neue Zufallsgröße $Z = A \cdot Y$ betrachtet. Der WDF–Parameter $A$ ist dabei so zu bestimmen, dass die differentielle Entropie der neuen Zufallsgröße $Z$ genau $1$ bit ergibt:<br> |
:$$h(Z) = h (A \cdot Y) = h (Y) + {\rm log}_2 \hspace{0.1cm} (A) = 1\,{\rm bit} \hspace{0.05cm}.$$ | :$$h(Z) = h (A \cdot Y) = h (Y) + {\rm log}_2 \hspace{0.1cm} (A) = 1\,{\rm bit} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| Line 44: | Line 45: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie die differentielle Entropie der Zufallsgröße $X$ in „nat”. | + | {Berechnen Sie die differentielle Entropie der Zufallsgröße $X$ in „nat”. |
|type="{}"} | |type="{}"} | ||
$h(X) \ = \ $ { -0.199--0.187 } $\ \rm nat$ | $h(X) \ = \ $ { -0.199--0.187 } $\ \rm nat$ | ||
| − | {Welches Ergebnis erhält man mit der Pseudoeinheit „bit”? | + | {Welches Ergebnis erhält man mit der Pseudoeinheit „bit”? |
|type="{}"} | |type="{}"} | ||
$h(X) \ = \ $ { -0.288--0.270 } $\ \rm bit$ | $h(X) \ = \ $ { -0.288--0.270 } $\ \rm bit$ | ||
| − | {Berechnen Sie die differentielle Entropie der Zufallsgröße $Y$. | + | {Berechnen Sie die differentielle Entropie der Zufallsgröße $Y$. |
|type="{}"} | |type="{}"} | ||
$h(Y) \ = \ $ { 0.721 3% } $\ \rm bit$ | $h(Y) \ = \ $ { 0.721 3% } $\ \rm bit$ | ||
| − | {Bestimmen Sie den WDF–Parameter $A$, | + | {Bestimmen Sie den WDF–Parameter $A$ derart, dass $\underline{h(Z) = h (A \cdot Y) = 1 \ \rm bit}$ gilt. |
|type="{}"} | |type="{}"} | ||
$A\ = $ { 1.213 3% } | $A\ = $ { 1.213 3% } | ||
Revision as of 17:14, 10 February 2020
Betrachtet werden zwei Wahrscheinlichkeitsdichtefunktionen (kurz WDF) mit dreieckförmigem Verlauf.
- Die Zufallsgröße $X$ ist auf den Wertebereich von $0$ bis $1$ begrenzt, und es gilt für die WDF (obere Skizze):
- $$f_X(x) = \left\{ \begin{array}{c} 2x \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 1 \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.$$
- Die Zufallsgröße $Y$ besitzt gemäß der unteren Skizze die folgende WDF:
- $$f_Y(y) = \left\{ \begin{array}{c} 1 - |\hspace{0.03cm}y\hspace{0.03cm}| \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |\hspace{0.03cm}y\hspace{0.03cm}| \le 1 \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.$$
Für beide Zufallsgrößen soll jeweils die differentielle Entropie ermittelt werden.
Beispielsweise lautet die entsprechende Gleichung für die Zufallsgröße $X$:
- $$h(X) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [ f_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.6cm}{\rm mit}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} \hspace{0.05cm}.$$
- Verwendet man den natürlichen Logarithmus, so ist die Pseudo–Einheit „nat” anzufügen.
- Ist das Ergebnis dagegen in „bit” gefragt, so ist der Logarithmus dualis ⇒ „$\log_2$” zu verwenden.
In der vierten Teilaufgabe wird die neue Zufallsgröße $Z = A \cdot Y$ betrachtet. Der WDF–Parameter $A$ ist dabei so zu bestimmen, dass die differentielle Entropie der neuen Zufallsgröße $Z$ genau $1$ bit ergibt:
- $$h(Z) = h (A \cdot Y) = h (Y) + {\rm log}_2 \hspace{0.1cm} (A) = 1\,{\rm bit} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Differentielle Entropie.
- Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im dritten Kapitel „Kontinuierliche Zufallsgrößen” des Buches Stochastische Signaltheorie.
- Vorgegeben ist das folgende unbestimmte Integral:
- $$\int \xi \cdot {\rm ln} \hspace{0.1cm} (\xi)\hspace{0.1cm}{\rm d}\xi = \xi^2 \cdot \big [1/2 \cdot {{\rm ln} \hspace{0.1cm} (\xi)} - {1}/{4}\big ] \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$f_X(x) = 2x = C \cdot x \hspace{0.05cm}.$$
- Wir haben hierbei „2” durch $C$ ersetzt ⇒ Verallgemeinerung, um in der Teilaufgabe $(3)$ die nachfolgende Berechnung nochmals nutzen zu können.
- Da die differentielle Entropie in „nat” gesucht ist, verwenden wir den natürlichen Logarithmus. Mit der Substitution $\xi = C \cdot x$ erhalten wir:
- $$h_{\rm nat}(X) = \hspace{0.1cm} - \int_{0}^{1} \hspace{0.1cm} C \cdot x \cdot {\rm ln} \hspace{0.1cm} \big[ C \cdot x \big] \hspace{0.1cm}{\rm d}x = \hspace{0.1cm} - \hspace{0.1cm}\frac{1}{C} \cdot \int_{0}^{C} \hspace{0.1cm} \xi \cdot {\rm ln} \hspace{0.1cm} [ \xi ] \hspace{0.1cm}{\rm d}\xi = - \hspace{0.1cm}\frac{\xi^2}{C} \cdot \left [ \frac{{\rm ln} \hspace{0.1cm} (\xi)}{2} - \frac{1}{4}\right ]_{\xi = 0}^{\xi = C} \hspace{0.05cm}$$
- Hierbei wurde das vorne angegebene unbestimmte Integral benutzt. Nach Einsetzen der Grenzen erhält man unter Berücksichtigung von $C=2$:
- $$h_{\rm nat}(X) = - C/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (C) - 1/2 \big ] = - {\rm ln} \hspace{0.1cm} (2) + 1/2 = - {\rm ln} \hspace{0.1cm} (2) + 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (\sqrt{\rm e}/2)\hspace{0.05cm} = - 0.193 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(X) \hspace{0.15cm}\underline {= - 0.193\,{\rm nat}} \hspace{0.05cm}.$$
(2) Allgemein gilt:
- $$h_{\rm bit}(X) = \frac{h_{\rm nat}(X)}{{\rm ln} \hspace{0.1cm} (2)\,{\rm nat/bit}} = - 0.279 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(X) \hspace{0.15cm}\underline {= - 0.279\,{\rm bit}} \hspace{0.05cm}.$$
Diese Umrechnung kann man sich sparen, wenn man bereits im analytischen Ergebnis der Teilaufgabe (1) direkt „ln” durch „log2” ersetzt:
- $$h(X) = \ {\rm log}_2 \hspace{0.1cm} (\sqrt{\rm e}/2)\hspace{0.05cm}, \hspace{1.3cm} {\rm Pseudo-Einheit\hspace{-0.1cm}:\hspace{0.15cm} bit} \hspace{0.05cm}.$$
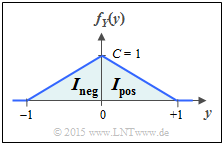
(3) Wir verwenden wieder den natürlichen Logarithmus und teilen das Integral in zwei Teilintegrale auf:
- $$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp} \hspace{0.03cm}( \hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm ln} \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y = I_{\rm neg} + I_{\rm pos} \hspace{0.05cm}.$$
- Das erste Integral für den Bereich $-1 \le y \le 0$ ist formgleich mit dem der Teilaufgabe $(1)$ und gegenüber diesem nur verschoben, was das Ergebnis nicht beeinflusst. Zu berücksichtigen ist nun die Höhe $C = 1$ anstelle von $C = 2$:
- $$I_{\rm neg} =- C/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (C) - 1/2 \big ] = -1/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (1) - 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) \big ]= 1/4 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) \hspace{0.05cm}.$$
- Der zweite Integrand ist bis auf eine Verschiebung und Spiegelung identisch mit dem ersten. Außerdem überlappen sich die Integrationsintervalle nicht ⇒ $I_{\rm pos} = I_{\rm neg}$:
- $$h_{\rm nat}(Y) = 2 \cdot I_{\rm neg} = 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (\sqrt{\rm e}) \hspace{0.3cm} \Rightarrow\hspace{0.3cm}h_{\rm bit}(Y) = {\rm log}_2 \hspace{0.1cm} (\sqrt{\rm e}) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(Y) = {\rm log}_2 \hspace{0.1cm} (1.649)\hspace{0.15cm}\underline {= 0.721\,{\rm bit}}\hspace{0.05cm}.$$
(4) Für die differentielle Entropie der Zufallsgröße $Z = A \cdot Y$ gilt allgemein:
- $$h(Z) = h(A \cdot Y) = h(Y) + {\rm log}_2 \hspace{0.1cm} (A) \hspace{0.05cm}.$$
Aus der Forderung $h(Z) = 1 \ \rm bit$ und dem Ergebnis der Teilaufgabe $(3)$ folgt somit:
- $${\rm log}_2 \hspace{0.1cm} (A) = 1\,{\rm bit} - 0.721 \,{\rm bit} = 0.279 \,{\rm bit} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} A = 2^{0.279}\hspace{0.15cm}\underline {= 1.213} \hspace{0.05cm}.$$