Aufgaben:Exercise 2.8: Asymmetrical Channel

• Return to book

Äquivalentes Tiefpass–Signal
in der komplexen Ebene

Ein cosinusförmiges Quellensignal  $q(t)$  mit der Amplitude  $A_{\rm N}$  und der Frequenz  $f_{\rm N}$  wird ZSB–amplitudenmoduliert, so dass für das modulierte Signal gilt:

$$s(t) = \big[ q(t) + A_{\rm T}\big] \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t ) \hspace{0.05cm}.$$

Der Übertragungskanal weist lineare Verzerrungen auf:

• Während das untere Seitenband $($USB-Frequenz:    $f_{\rm T} - f_{\rm N})$  und auch der Träger unverfälscht übertragen werden,
• wird das obere Seitenband $($OSB-Frequenz:    $f_{\rm T} + f_{\rm N})$  mit dem Dämpfungsfaktor  $α_{\rm O} = 0.25$  gewichtet.

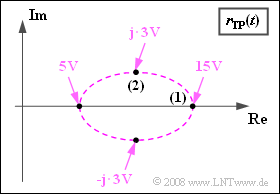
Die Grafik zeigt die Ortskurve, also die Darstellung des äquivalenten Tiefpass–Signals  $r_{\rm TP}(t)$  in der komplexen Ebene.

Wertet man das Signal  $r(t)$  mit einem idealen Hüllkurvendemodulator aus, so erhält man ein Sinkensignal  $v(t)$, das wie folgt angenähert werden kann:

$$v(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t ) -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t )-\text{ ...}$$

Für diese Messung wurde die Nachrichtenfrequenz  $f_{\rm N} = 2 \ \rm kHz$  benutzt.

In der Teilaufgabe  (7)  soll das Signal–zu–Stör–Leistungsverhältnis  $\rm (SNR)$  wie folgt berechnet werden:

$$\rho_{v } = \frac{P_{v 1}}{P_{\varepsilon }} \hspace{0.05cm}.$$

Hierbei bezeichnen  $P_{v1} = α^2 · P_q$  und  $P_ε$  die „Leistungen” der beiden Signale:

$$v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$

$$\varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Hüllkurvendemodulation.
• Bezug genommen wird insbesondere auf das Kapitel  Beschreibung mit Hilfe des äquivalenten Tiefpass-Signals.

Fragebogen

1

Geben Sie das Tiefpass-Signal  $r_{\rm TP}(t)$  in analytischer Form an.  Welcher Wert ergibt sich für die Zeit  $t = 0$?

$r_{\rm TP}(t=0) \ = \ $ $\ \rm V$

2

Wie lauten die Amplitudenwerte  $A_{\rm T}$  und  $A_{\rm N}$?

$A_{\rm T} \ = \ $ $\ \rm V$

$A_{\rm N} \ = \ $ $\ \rm V$

3

Es gelte  $f_{\rm N} \hspace{0.15cm}\underline{= 2 \ \rm kHz}$.  Zu welcher Zeit  $t_1$  wird der Startpunkt  (1)  zum ersten Mal nach  $t = 0$  wieder erreicht?

$t_1 \ = \ $ $\ \rm ms$

4

Zu welchem Zeitpunkt  $t_2$  wird der Ellipsenpunkt  (2)  mit dem Wert  $\rm j · 3\ V$  zum ersten Mal erreicht?

$t_2 \ = \ $ $\ \rm ms$

5

Berechnen Sie die Betragsfunktion (Hüllkurve)  $a(t)$  und die Phasenfunktion  $ϕ(t)$  für diesen Zeitpunkt  $t_2$.

$a(t = t_2) \ = \ $ $\ \rm V$

$ϕ(t = t_2)\ = \ $ $\ \rm Grad$

6

Berechnen Sie den Klirrfaktor  $K$  für  $f_{\rm N} \hspace{0.15cm}\underline{= 2 \ \rm kHz}$.

$K \ = \ $ $\ \text{%}$

7

Berechnen Sie für  $f_{\rm N}\hspace{0.15cm}\underline{ = 2 \ \rm kHz}$  das Signal–zu–Stör–Leistungsverhältnis  $\rm (SNR)$  gemäß der angegebenen Definition.

$ρ_v \ = \ $

8

Welcher Klirrfaktor  $K$  ergibt sich bei ansonsten gleichen Bedingungen mit der Nachrichtenfrequenz  $f_{\rm N} \hspace{0.15cm}\underline{= 4 \ \rm kHz}$?

$K \ = \ $ $\ \text{%}$

Musterlösung

Solution

(1)  Bei cosinusförmigem Quellensignal und Dämpfung des oberen Seitenbandes gilt:

$$r_{\rm TP}(t) = A_{\rm T} + \frac{A_{\rm N}}{2} \cdot \alpha_{\rm O} \cdot{\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm N}\cdot t} + \frac{A_{\rm N}}{2} \cdot{\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm N}\cdot t}\hspace{0.05cm}.$$

• Zum Zeitpunkt  $t = 0$  zeigen alle Vektoren in Richtung der reellen Achse.
• Somit kann aus der Grafik auf der Angabenseite  $r_{\rm TP}(t = 0)\hspace{0.15cm}\underline { = 15 \ \rm V}$  abgelesen werden.

(2)  Die Trägeramplitude ist durch den Ellipsenmittelpunkt festgelegt:  $A_{\rm T}\hspace{0.15cm}\underline { = 10 \ \rm V}$.

• Aus der in der ersten Teilaufgabe angegebenen Gleichung kann somit auch die Amplitude  $A_{\rm N}$  berechnet werden:

$$\frac{A_{\rm N}}{2} \cdot ( 1+ \alpha_0) = r_{\rm TP}(t= 0) - A_{\rm T} = 5 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm N} \hspace{0.15cm}\underline {= 8 \,{\rm V}} \hspace{0.05cm}.$$

• Zur Kontrolle kann der in der Grafik markierte Punkt  (2)  herangezogen werden:

$$\frac{A_{\rm N}}{2} \cdot ( 1- \alpha_0) = 3 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm N} = 8 \,{\rm V} \hspace{0.05cm}.$$

(3)  Die für einen Umlauf benötigte Zeit  $t_1$  ist gleich der Periodendauer des Quellensignals, also

$$t_1= 1/f_{\rm N} \hspace{0.15cm}\underline {=0.5 \ \rm ms}.$$

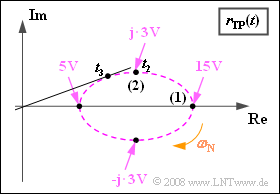
(4)  Da das USB größer ist als das OSB, bewegt sich die Spitze des Zeigerverbundes auf der Ellipse im Uhrzeigersinn.

• Der Punkt  (2)  wird zum Zeitpunkt  $t_2 = 3/4 · t_1\hspace{0.15cm}\underline { = 0.375 \ \rm ms}$  zum ersten Mal erreicht.

Zur Berechnung von  $t_2$  und  $t_3$

(5)  Die Zeigerlänge zur Zeit  $t_2$  kann mit dem  Satz von Pythagoras  bestimmt werden:

$$a(t = t_2) = \sqrt{(10 \,{\rm V})^2 + (3 \,{\rm V})^2}\hspace{0.15cm}\underline { = 10.44 \,{\rm V}}\hspace{0.05cm}.$$

• Für die Phasenfunktion gilt:

$$\phi(t = t_2) = {\rm arctan} \frac{3 \,{\rm V}}{10 \,{\rm V}} \hspace{0.15cm}\underline {= 16.7^{\circ}}\hspace{0.05cm}.$$

• Die maximale Phase  $ϕ_{\rm max}$  ist geringfügig größer.  Sie tritt (mit positivem Vorzeichen) zum Zeitpunkt  $t_3 < t_2$  dann auf, wenn eine Gerade vom Koordinatenursprung die Ellipse tangiert.
• Durch Aufstellen der Ellipsengleichung kann dieser Punkt  $(x_3$,  $y_3)$  analytisch exakt berechnet werden.
• Daraus würde für die maximale Phase gelten:  $\phi_{\rm max} = {\rm arctan} \ {y_3}/{x_3} \hspace{0.05cm}.$

(6)  Die Klirrfaktoren zweiter und dritter Ordnung können aus der angegebenen Gleichung für  $v(t)$  $($gültig für $f_{\rm N} = 2 \ \rm kHz)$  ermittelt werden und lauten:

$$K_2 = \frac{0.148 \,{\rm V}}{2.424 \,{\rm V}} = 0.061, \hspace{0.3cm} K_3 = \frac{0.056 \,{\rm V}}{2.424 \,{\rm V}} = 0.023 \hspace{0.05cm}.$$

• Damit erhält man für den Gesamtklirrfaktor:

$$K = \sqrt{K_2^2 + K_3^2 }\hspace{0.15cm}\underline { \approx 6.6 \%}.$$

(7)  Für die Leistungen von Nutz– und Störsignal erhält man:

$$P_{v 1} = \frac{(2.424 \,{\rm V})^2}{2} = 2.94 \,{\rm V}^2\hspace{0.05cm},\hspace{0.3cm} P_{\varepsilon} = \frac{(-0.148 \,{\rm V})^2}{2} + \frac{(0.056 \,{\rm V})^2}{2}= 0.0125 \,{\rm V}^2\hspace{0.05cm}$$

• Damit ergibt sich für das Signal–zu–Stör–Leistungsverhältnis  $\rm (SNR)$:

$$\rho_{v} = \frac{P_{v 1}}{P_{\varepsilon }}= \frac{(2.94 \,{\rm V})^2}{0.0125 \,{\rm V}^2} \hspace{0.15cm}\underline {\approx 230} = \frac{1}{K^2} \hspace{0.05cm}.$$

• Würde man dagegen die Amplitudenverfälschung ebenfalls dem Fehlersignal zuweisen, so käme man zu einem deutlich kleineren  $\rm SNR$.   
• Mit $P_q = A_{\rm N}^2/2 = 8 \ \rm V^2$  und  $P_{\varepsilon}\hspace{0.02cm}' = \overline{(v(t)-q(t))^2} = {1}/{2}\cdot ( 4 \,{\rm V} - 2.424 \,{\rm V})^2 + P_{\varepsilon}= 1.254 \,{\rm V}^2$  würde man dann erhalten:

$$\rho_{v }\hspace{0.02cm}' = \frac{8 \,{\rm V}^2}{1.254 \,{\rm V}^2} \approx 6.4\hspace{0.05cm}.$$

(8)  Alle Berechnungen gelten unabhängig von der Nachrichtenfrequenz  $f_{\rm N}$, wenn der Dämpfungsfaktor des OSB weiterhin  $α_{\rm O} = 0.25$  beträgt.

• Damit erhält man auch für  $f_{\rm N} = 4 \ \rm kHz$  den gleichen Klirrfaktor  $K\hspace{0.15cm}\underline { \approx 6.6 \%}$.