Difference between revisions of "Aufgaben:Exercise 3.2: Spectrum with Angle Modulation"
| Line 74: | Line 74: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die Phase $ϕ(t)$ ist proportional zum Quellensignal $q(t)$ ⇒ es handelt sich um eine Phasenmodulation ⇒ <u>Antwort 2</u>. | + | '''(1)''' Die Phase $ϕ(t)$ ist proportional zum Quellensignal $q(t)$ ⇒ es handelt sich um eine Phasenmodulation ⇒ <u>Antwort 2</u>. |
| − | '''(2)''' Eine Winkelmodulation (PM, FM) führt bei bandbegrenztem Kanal stets zu nichtlinearen Verzerrungen. | + | '''(2)''' Eine Winkelmodulation (PM, FM) führt bei bandbegrenztem Kanal stets zu nichtlinearen Verzerrungen. |
| − | *Bei Zweiseitenband-Amplitudenmodulation (ZSB-AM) ist hier dagegen bereits mit $B_{\rm K} = 6 \ \rm kHz$ eine verzerrungsfreie Übertragung möglich ⇒ <u>Antwort 1</u>. | + | *Bei Zweiseitenband-Amplitudenmodulation (ZSB-AM) ist hier dagegen bereits mit $B_{\rm K} = 6 \ \rm kHz$ eine verzerrungsfreie Übertragung möglich ⇒ <u>Antwort 1</u>. |
| − | '''(3)''' Der Modulationsindex (oder Phasenhub) ist bei Phasenmodulation gleich $η = K_{\rm M} · A_{\rm N}$. | + | '''(3)''' Der Modulationsindex (oder Phasenhub) ist bei Phasenmodulation gleich $η = K_{\rm M} · A_{\rm N}$. |
| − | *Somit ist die Modulatorkonstante $K_{\rm M} = 1/A_{\rm N}\hspace{0.15cm}\underline { = 0.5 \rm \cdot {1}/{V}}$ zu wählen, damit sich $η = 1$ ergibt. | + | *Somit ist die Modulatorkonstante $K_{\rm M} = 1/A_{\rm N}\hspace{0.15cm}\underline { = 0.5 \rm \cdot {1}/{V}}$ zu wählen, damit sich $η = 1$ ergibt. |
| Line 90: | Line 90: | ||
'''(4)''' Es liegt ein sogenanntes Besselspektrum vor: | '''(4)''' Es liegt ein sogenanntes Besselspektrum vor: | ||
:$$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$ | :$$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$ | ||
| − | *Dieses ist ein diskretes Spektrum mit Anteilen bei $f = n · f_{\rm N}$, wobei $n$ ganzzahlig ist. | + | *Dieses ist ein diskretes Spektrum mit Anteilen bei $f = n · f_{\rm N}$, wobei $n$ ganzzahlig ist. |
| − | *Die Gewichte der Diracfunktionen sind durch die Besselfunktionen gegeben. Mit $A_{\rm T} = 1\ \rm V$ erhält man: | + | *Die Gewichte der Diracfunktionen sind durch die Besselfunktionen gegeben. Mit $A_{\rm T} = 1\ \rm V$ erhält man: |
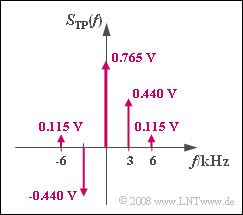
[[File:P_ID1082__Mod_A_3_2_d.png|right|frame|PM–Spektrum im äquivalenten Tiefpass–Bereich]] | [[File:P_ID1082__Mod_A_3_2_d.png|right|frame|PM–Spektrum im äquivalenten Tiefpass–Bereich]] | ||
:$$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$ | :$$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$ | ||
:$$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$ | :$$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$ | ||
:$$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$ | :$$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$ | ||
| − | *Aufgrund der Symmetrie ${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$ erhält man für die Spektrallinie bei $f = -3 \ \rm kHz$: | + | *Aufgrund der Symmetrie ${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$ erhält man für die Spektrallinie bei $f = -3 \ \rm kHz$: |
:$$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$ | :$$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$ | ||
| − | ''Anmerkung'': Eigentlich müsste man für den Spektralwert bei $f = 0$ schreiben: | + | ''Anmerkung'': Eigentlich müsste man für den Spektralwert bei $f = 0$ schreiben: |
:$$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$ | :$$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$ | ||
| − | Dieser ist somit aufgrund der Diracfunktion unendlich groß, lediglich das Gewicht der Diracfunktion ist endlich. Gleiches gilt für alle diskreten Spektrallinien. | + | *Dieser ist somit aufgrund der Diracfunktion unendlich groß, lediglich das Gewicht der Diracfunktion ist endlich. |
| + | *Gleiches gilt für alle diskreten Spektrallinien. | ||
| − | '''(5)''' $S_+(f)$ ergibt sich aus $S_{\rm TP}(f)$ durch Verschiebung um $f_{\rm T}$ nach rechts. Deshalb ist | + | '''(5)''' $S_+(f)$ ergibt sich aus $S_{\rm TP}(f)$ durch Verschiebung um $f_{\rm T}$ nach rechts. Deshalb ist |
:$$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$ | :$$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$ | ||
| − | *Das tatsächliche Spektrum unterscheidet sich von $S_+(f)$ bei positiven Frequenzen um den Faktor $1/2$: | + | *Das tatsächliche Spektrum unterscheidet sich von $S_+(f)$ bei positiven Frequenzen um den Faktor $1/2$: |
:$$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$ | :$$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$ | ||
*Allgemein kann geschrieben werden: | *Allgemein kann geschrieben werden: | ||
| Line 112: | Line 113: | ||
| − | '''(6)''' Unter der vorgeschlagenen Vernachlässigung können alle Bessellinien ${\rm J}_{|n|>3}$ außer Acht gelassen werden. | + | |
| − | * Damit erhält man $B_{\rm K} = 2 · 3 · f_{\rm N}\hspace{0.15cm}\underline { = 18 \ \rm kHz}$. | + | '''(6)''' Unter der vorgeschlagenen Vernachlässigung können alle Bessellinien ${\rm J}_{|n|>3}$ außer Acht gelassen werden. |
| + | * Damit erhält man $B_{\rm K} = 2 · 3 · f_{\rm N}\hspace{0.15cm}\underline { = 18 \ \rm kHz}$. | ||
Revision as of 17:16, 24 March 2020
Es wird hier von folgenden Gleichungen ausgegangen:
- Quellensignal:
- $$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$
- Sendesignal:
- $$s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + K_{\rm M} \cdot q(t)\big ]\hspace{0.05cm},$$
- Empfangssignal (idealer Kanal:
- $$r(t) = s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + \phi(t)\big ]\hspace{0.05cm},$$
- idealer Demodulator:
- $$ v(t) = \frac{1}{ K_{\rm M}} \cdot \phi(t)\hspace{0.05cm}.$$
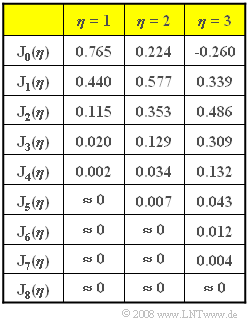
Die Grafik zeigt die Besselfunktionen ${\rm J}_n (\eta)$ erster Art und $n$–ter Ordnung in tabellarischer Form.
Hinweise:
- Die Aufgabe gehört zum Kapitel Phasenmodulation.
- Bezug genommen wird insbesondere auf die Seiten Spektralfunktion eines phasenmodulierten Sinussignals sowie Interpretation des Besselspektrums.
Fragebogen
Musterlösung
(2) Eine Winkelmodulation (PM, FM) führt bei bandbegrenztem Kanal stets zu nichtlinearen Verzerrungen.
- Bei Zweiseitenband-Amplitudenmodulation (ZSB-AM) ist hier dagegen bereits mit $B_{\rm K} = 6 \ \rm kHz$ eine verzerrungsfreie Übertragung möglich ⇒ Antwort 1.
(3) Der Modulationsindex (oder Phasenhub) ist bei Phasenmodulation gleich $η = K_{\rm M} · A_{\rm N}$.
- Somit ist die Modulatorkonstante $K_{\rm M} = 1/A_{\rm N}\hspace{0.15cm}\underline { = 0.5 \rm \cdot {1}/{V}}$ zu wählen, damit sich $η = 1$ ergibt.
(4) Es liegt ein sogenanntes Besselspektrum vor:
- $$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$
- Dieses ist ein diskretes Spektrum mit Anteilen bei $f = n · f_{\rm N}$, wobei $n$ ganzzahlig ist.
- Die Gewichte der Diracfunktionen sind durch die Besselfunktionen gegeben. Mit $A_{\rm T} = 1\ \rm V$ erhält man:
- $$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$
- $$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$
- $$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$
- Aufgrund der Symmetrie ${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$ erhält man für die Spektrallinie bei $f = -3 \ \rm kHz$:
- $$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$
Anmerkung: Eigentlich müsste man für den Spektralwert bei $f = 0$ schreiben:
- $$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$
- Dieser ist somit aufgrund der Diracfunktion unendlich groß, lediglich das Gewicht der Diracfunktion ist endlich.
- Gleiches gilt für alle diskreten Spektrallinien.
(5) $S_+(f)$ ergibt sich aus $S_{\rm TP}(f)$ durch Verschiebung um $f_{\rm T}$ nach rechts. Deshalb ist
- $$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$
- Das tatsächliche Spektrum unterscheidet sich von $S_+(f)$ bei positiven Frequenzen um den Faktor $1/2$:
- $$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$
- Allgemein kann geschrieben werden:
- $$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$
(6) Unter der vorgeschlagenen Vernachlässigung können alle Bessellinien ${\rm J}_{|n|>3}$ außer Acht gelassen werden.
- Damit erhält man $B_{\rm K} = 2 · 3 · f_{\rm N}\hspace{0.15cm}\underline { = 18 \ \rm kHz}$.
(7) Die Zahlenwerte in der Tabelle auf der Angabenseite zeigen, dass nun folgende Kanalbandbreiten erforderlich wären:
- für $η = 2$: $B_{\rm K} \hspace{0.15cm}\underline { = 24 \ \rm kHz}$,
- für $η = 3$: $B_{\rm K} \hspace{0.15cm}\underline { = 36 \ \rm kHz}$.