Difference between revisions of "Aufgaben:Exercise 1.1Z: Simple Path Loss Model"
m (Javier verschob die Seite Exercises:Exercise 1.1Z: Simple Path Loss Model nach Exercise 1.1Z: Simple Path Loss Model) |
|||
| Line 3: | Line 3: | ||
[[File:P_ID2121__Mob_Z_1_1.png|right|frame|Bandbreitenorganisation bei DSL]] | [[File:P_ID2121__Mob_Z_1_1.png|right|frame|Bandbreitenorganisation bei DSL]] | ||
| − | + | Radio transmission with line-of-sight can be described by the so-called path loss model, which is given by the following equations: | |
| − | + | $$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},$$ | |
| − | + | $$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$ | |
| − | + | The graphic shows the path loss $V_{\rm P}(d)$ in $\rm dB$. The abscissa $d$ is also displayed logarithmically. | |
| − | In | + | In the above equation are used: |
| − | * | + | * the distance $d$ of sender and receiver, |
| − | * | + | * the reference distance $d_0 = 1 \ \rm m$, |
| − | * | + | * the path loss exponent $\gamma$, |
| − | * | + | * the wavelength $\lambda$ of electromagnetic wave. |
| − | + | Two scenarios are shown $\rm (A)$ and $\rm (B)$ with the same path loss at distance $d_0 = 1 \ \rm m$: | |
| − | + | $$V_{\rm 0} = V_{\rm P}(d = d_0) = 20\,{\rm dB} \hspace{0.05cm}.$$ | |
| − | + | One of these two scenarios describes the so-called <i>free space attenuation</i>, characterized by the path loss exponent $\gamma = 2$. However, the equation for the free space attenuation only applies in the <i>far-field</i>, i.e. when the distance $d$ between transmitter and receiver is greater than the „Fraunhofer–distance” | |
| − | + | $$d_{\rm F} = {2 D^2}/{\lambda} \hspace{0.05cm}.$$ | |
| − | + | Where $D$ is the largest physical dimension of the transmitting antenna. With an $\lambda/2$–antenna, you get the simple result for this: | |
| − | + | $$d_{\rm F} = \frac{2 \cdot (\lambda/2)^2}{\lambda} = {\lambda}/{2}\hspace{0.05cm}.$$ | |
| Line 30: | Line 30: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * The task belongs to the chapter [[Mobile_Communication/Distancedependent%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Distance-dependent attenuation and shading]]. |
| − | * | + | * The speed of light is $c = 3 \cdot 10^8 \ {\rm m/s}$. |
| Line 38: | Line 38: | ||
| − | === | + | ===Questionnaire=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which path loss exponents apply to the scenarios $\rm (A)$ and $\rm (B)$? |
|type="{}"} | |type="{}"} | ||
$\gamma_{\rm A}\ = \ $ { 2 3% } | $\gamma_{\rm A}\ = \ $ { 2 3% } | ||
$\gamma_{\rm B} \ = \ $ { 2.5 3% } | $\gamma_{\rm B} \ = \ $ { 2.5 3% } | ||
| − | { | + | {Which scenario describes the free space attenuation? |
|type="()"} | |type="()"} | ||
| − | + | + | + scenario $\rm (A)$, |
| − | - | + | - Scenario $\rm (B)$. |
| − | { | + | {Which signal frequencies are the basis for the scenarios $\rm (A)$ and $\rm (B)$ ? |
|type="{}"} | |type="{}"} | ||
| − | $f_{\rm A} \ = \ $ { 240 3% } $\ \rm MHz$ | + | $f_{\rm A} \ = \ $ { 240 3% } $\ \ \rm MHz$ |
| − | $f_{\rm B} \ = \ $ { 151.4 3% } $\ \rm MHz$ | + | $f_{\rm B} \ = \ $ { 151.4 3% } $\ \ \rm MHz$ |
| − | + | Does the free space&ndash scenario apply to all distances between $1 \ \ \rm m$ and $10 \ \rm km$? | |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes, |
| − | - | + | - No. |
</quiz> | </quiz> | ||
| − | === | + | ===Sample solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1) | + | '''(1)'' The (simplest) path loss equation is |
| − | + | $$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm}.$$ | |
| − | * | + | *In scenario (A), the waste per decade (for example, between $d_0 = 1 \ \rm m$ and $d = 10 \ \rm m$) is exactly $20 \ \rm dB$ and in scenario (B) $25 \ \rm dB$. |
| − | * | + | *It follows: |
| − | + | $$\gamma_{\rm A} \hspace{0.15cm} \underline{= 2}\hspace{0.05cm},\hspace{0.2cm}\gamma_{\rm B} \hspace{0.15cm} \underline{= 2.5}\hspace{0.05cm}.$$ | |
| − | '''(2)''' | + | '''(2)''' Correct is <u>solution 1</u>, since the free space attenuation is characterized by the path loss exponent $\gamma = 2$. |
| − | '''(3)''' | + | '''(3)''' The path loss at $d_0 = 1 \ \rm m$ is in both cases $V_0 = 20 \ \rm dB$. For scenario (A) the same applies: |
| − | + | $$10 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}}\right ]^2 = 20\,{\rm dB} \hspace{0.2cm} \Rightarrow \hspace{0.2cm} | |
\frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}} = 10 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} | \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}} = 10 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} | ||
| − | \lambda_{\rm A} = 4 | + | \lambda_{\rm A} = 4 \pi \cdot 0.1\,{\rm m} = 1,257\,{\rm m} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The frequency $f_{\rm A}$ is related to the wavelength $\lambda_{\rm A}$ over the speed of light $c$: |
| − | + | $$f_{\rm A} = \frac{c}{\lambda_{\rm A}} = \frac{3 \cdot 10^8\,{\rm m/s}}}{1.257\,{\rm m}} = 2.39 \cdot 10^8\,{\rm Hz} | |
| − | \hspace{0.15cm} \underline{\approx | + | \hspace{0.15cm} \underline{\approx 240 \,\,{\rm MHz}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *On the other hand, the scenario (B) |
| − | + | $$10 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}}\right ]^{2.5} = 20\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 25 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}}\right ] = 20\,{\rm dB}$$ | |
| − | + | $$\Rightarrow \hspace{0.3cm} \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}} = 10^{0.8} \approx 6.31 | |
| − | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | + | \hspace {0.3cm} \Rightarrow \hspace{0.3cm} |
{\lambda_{\rm B}} = \frac{10}{6.31} \cdot {\lambda_{\rm A}}\hspace{0.3cm} | {\lambda_{\rm B}} = \frac{10}{6.31} \cdot {\lambda_{\rm A}}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} | \Rightarrow \hspace{0.3cm} | ||
| − | {f_{\rm B}} = \frac{6.31}{10} \cdot {f_{\rm A}} = 0.631 \cdot 240 \,{\rm MHz}\hspace{0.15cm} \underline{\approx | + | {f_{\rm B}}} = \frac{6.31}{10} \cdot {f_{\rm A}}} = 0.631 \cdot 240 \,{\rm MHz}\hspace{0.15cm} \underline {\approx 151.4 \,\,{\rm MHz}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' <u>first suggested solution</u> is correct: |
| − | * | + | *In free space–scenario (A) the Fraunhofer–distance $d_{\rm F} = \lambda_{\rm A}/2 \approx 63 \ \rm cm$. Thus, the following always applies $d > d_{\rm F}$. |
| − | * | + | *Also in scenario (B) is because of $\lambda_{\rm B} \approx 2 \ \rm m$ or $d_{\rm F} \approx 1 \ \rm m$ the entire displayed course correct. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 15:44, 25 March 2020
Radio transmission with line-of-sight can be described by the so-called path loss model, which is given by the following equations: $$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},$$ $$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$
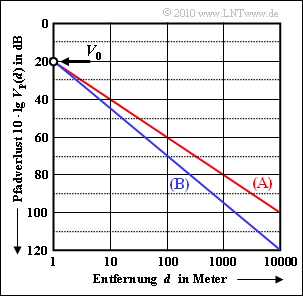
The graphic shows the path loss $V_{\rm P}(d)$ in $\rm dB$. The abscissa $d$ is also displayed logarithmically.
In the above equation are used:
- the distance $d$ of sender and receiver,
- the reference distance $d_0 = 1 \ \rm m$,
- the path loss exponent $\gamma$,
- the wavelength $\lambda$ of electromagnetic wave.
Two scenarios are shown $\rm (A)$ and $\rm (B)$ with the same path loss at distance $d_0 = 1 \ \rm m$:
$$V_{\rm 0} = V_{\rm P}(d = d_0) = 20\,{\rm dB} \hspace{0.05cm}.$$
One of these two scenarios describes the so-called free space attenuation, characterized by the path loss exponent $\gamma = 2$. However, the equation for the free space attenuation only applies in the far-field, i.e. when the distance $d$ between transmitter and receiver is greater than the „Fraunhofer–distance” $$d_{\rm F} = {2 D^2}/{\lambda} \hspace{0.05cm}.$$
Where $D$ is the largest physical dimension of the transmitting antenna. With an $\lambda/2$–antenna, you get the simple result for this: $$d_{\rm F} = \frac{2 \cdot (\lambda/2)^2}{\lambda} = {\lambda}/{2}\hspace{0.05cm}.$$
Notes:
- The task belongs to the chapter Distance-dependent attenuation and shading.
- The speed of light is $c = 3 \cdot 10^8 \ {\rm m/s}$.
Questionnaire
Sample solution
- In scenario (A), the waste per decade (for example, between $d_0 = 1 \ \rm m$ and $d = 10 \ \rm m$) is exactly $20 \ \rm dB$ and in scenario (B) $25 \ \rm dB$.
- It follows:
$$\gamma_{\rm A} \hspace{0.15cm} \underline{= 2}\hspace{0.05cm},\hspace{0.2cm}\gamma_{\rm B} \hspace{0.15cm} \underline{= 2.5}\hspace{0.05cm}.$$
(2) Correct is solution 1, since the free space attenuation is characterized by the path loss exponent $\gamma = 2$.
(3) The path loss at $d_0 = 1 \ \rm m$ is in both cases $V_0 = 20 \ \rm dB$. For scenario (A) the same applies: $$10 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}}\right ]^2 = 20\,{\rm dB} \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}} = 10 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \lambda_{\rm A} = 4 \pi \cdot 0.1\,{\rm m} = 1,257\,{\rm m} \hspace{0.05cm}.$$
- The frequency $f_{\rm A}$ is related to the wavelength $\lambda_{\rm A}$ over the speed of light $c$:
$$f_{\rm A} = \frac{c}{\lambda_{\rm A}} = \frac{3 \cdot 10^8\,{\rm m/s}}}{1.257\,{\rm m}} = 2.39 \cdot 10^8\,{\rm Hz} \hspace{0.15cm} \underline{\approx 240 \,\,{\rm MHz}} \hspace{0.05cm}.$$
- On the other hand, the scenario (B)
$$10 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}}\right ]^{2.5} = 20\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 25 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}}\right ] = 20\,{\rm dB}$$ $$\Rightarrow \hspace{0.3cm} \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}} = 10^{0.8} \approx 6.31 \hspace {0.3cm} \Rightarrow \hspace{0.3cm} {\lambda_{\rm B}} = \frac{10}{6.31} \cdot {\lambda_{\rm A}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {f_{\rm B}}} = \frac{6.31}{10} \cdot {f_{\rm A}}} = 0.631 \cdot 240 \,{\rm MHz}\hspace{0.15cm} \underline {\approx 151.4 \,\,{\rm MHz}} \hspace{0.05cm}.$$
(4) first suggested solution is correct:
- In free space–scenario (A) the Fraunhofer–distance $d_{\rm F} = \lambda_{\rm A}/2 \approx 63 \ \rm cm$. Thus, the following always applies $d > d_{\rm F}$.
- Also in scenario (B) is because of $\lambda_{\rm B} \approx 2 \ \rm m$ or $d_{\rm F} \approx 1 \ \rm m$ the entire displayed course correct.