Difference between revisions of "Aufgaben:Exercise 4.3: Natural and Discrete Sampling"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1615__Mod_A_4_3.png|right|frame| | + | [[File:P_ID1615__Mod_A_4_3.png|right|frame|Zur natürlichen und diskreten Abtastung]] |
| − | Die ideale Abtastung lässt sich im Zeitbereich durch Multiplikation des analogen Quellensignals $q(t)$ mit einem [[Signaldarstellung/Zeitdiskrete_Signaldarstellung#Diracpuls_im_Zeit-_und_im_Frequenzbereich|Diracpuls]] $p_δ(t)$ beschreiben: | + | Die ideale Abtastung lässt sich im Zeitbereich durch Multiplikation des analogen Quellensignals $q(t)$ mit einem [[Signaldarstellung/Zeitdiskrete_Signaldarstellung#Diracpuls_im_Zeit-_und_im_Frequenzbereich|Diracpuls]] $p_δ(t)$ beschreiben: |
:$$ q_{\rm A}(t) = p_{\delta}(t) \cdot q(t) \hspace{0.05cm}.$$ | :$$ q_{\rm A}(t) = p_{\delta}(t) \cdot q(t) \hspace{0.05cm}.$$ | ||
| − | Diracimpulse – unendlich schmal und unendlich hoch – und dementsprechend auch der Diracpuls $p_δ(t)$ lassen sich in der Praxis jedoch nicht realisieren. Hier muss statt dessen vom Rechteckpuls $p_{\rm R}(t)$ ausgegangen werden, wobei folgender Zusammenhang gilt: | + | Diracimpulse – unendlich schmal und unendlich hoch – und dementsprechend auch der Diracpuls $p_δ(t)$ lassen sich in der Praxis jedoch nicht realisieren. Hier muss statt dessen vom Rechteckpuls $p_{\rm R}(t)$ ausgegangen werden, wobei folgender Zusammenhang gilt: |
:$$ p_{\rm R}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \right ]\star g_{\rm R}(t)\hspace{0.9cm}\text{mit}\hspace{0.9cm} | :$$ p_{\rm R}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \right ]\star g_{\rm R}(t)\hspace{0.9cm}\text{mit}\hspace{0.9cm} | ||
g_{\rm R}(t) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} < T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} = T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.005cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} > T_{\rm R}/2\hspace{0.05cm}. \\ \end{array}$$ | g_{\rm R}(t) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} < T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} = T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.005cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} > T_{\rm R}/2\hspace{0.05cm}. \\ \end{array}$$ | ||
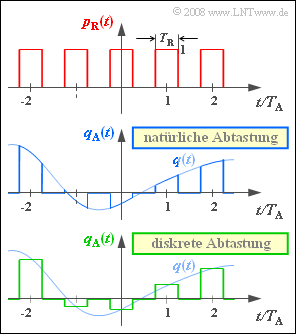
| − | Die Dauer $T_{\rm R}$ eines Rechteckimpulses $g_{\rm R}(t)$ sollte dabei (deutlich) kleiner sein als der Abstand $T_{\rm A}$ zweier Abtastwerte. In der Grafik ist dieses Verhältnis mit $T_{\rm R}/T_{\rm A} = 0.5$ sehr groß gewählt, um den Unterschied zwischen der | + | Die Dauer $T_{\rm R}$ eines Rechteckimpulses $g_{\rm R}(t)$ sollte dabei (deutlich) kleiner sein als der Abstand $T_{\rm A}$ zweier Abtastwerte. |
| + | |||
| + | In der Grafik ist dieses Verhältnis mit $T_{\rm R}/T_{\rm A} = 0.5$ sehr groß gewählt, um den Unterschied zwischen der „natürlichen Abtastung” und der „diskreten Abtastung” besonders deutlich werden zu lassen: | ||
* Bei natürlicher Abtastung ist das abgetastete Signal $q_{\rm A}(t)$ gleich dem Produkt aus Rechteckpuls $p_{\rm R}(t)$ und analogem Quellensignal $q(t)$: | * Bei natürlicher Abtastung ist das abgetastete Signal $q_{\rm A}(t)$ gleich dem Produkt aus Rechteckpuls $p_{\rm R}(t)$ und analogem Quellensignal $q(t)$: | ||
:$$q_{\rm A}(t) = p_{\rm R}(t) \cdot q(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t)\hspace{0.05cm}.$$ | :$$q_{\rm A}(t) = p_{\rm R}(t) \cdot q(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t)\hspace{0.05cm}.$$ | ||
| Line 15: | Line 17: | ||
:$$ q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \cdot q(t)\right ]\star g_{\rm R}(t)\hspace{0.05cm}.$$ | :$$ q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \cdot q(t)\right ]\star g_{\rm R}(t)\hspace{0.05cm}.$$ | ||
| − | In der Grafik sind diese Signale in blau (natürliche Abtastung) bzw. grün (diskrete Abtastung) skizziert. | + | In der Grafik sind diese Signale in blau (natürliche Abtastung) bzw. grün (diskrete Abtastung) skizziert. |
| − | Zur Signalrekonstruktion wird ein rechteckförmiger Tiefpass $H(f)$ mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2$ und der Verstärkung $T_{\rm A}/T_{\rm R}$ im Durchlassbereich eingesetzt: | + | Zur Signalrekonstruktion wird ein rechteckförmiger Tiefpass $H(f)$ mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2$ und der Verstärkung $T_{\rm A}/T_{\rm R}$ im Durchlassbereich eingesetzt: |
:$$H(f) = \left\{ \begin{array}{l} T_{\rm A}/T_{\rm R} \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2}\hspace{0.05cm}. \\ \end{array}$$ | :$$H(f) = \left\{ \begin{array}{l} T_{\rm A}/T_{\rm R} \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2}\hspace{0.05cm}. \\ \end{array}$$ | ||
| + | |||
| + | |||
| + | |||
| Line 28: | Line 33: | ||
*Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Pulscodemodulation|Pulscodemodulation]]. | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Pulscodemodulation|Pulscodemodulation]]. | ||
*Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Pulscodemodulation#Nat.C3.BCrliche_und_diskrete_Abtastung|Natürliche und diskrete Abtastung]]. | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Pulscodemodulation#Nat.C3.BCrliche_und_diskrete_Abtastung|Natürliche und diskrete Abtastung]]. | ||
| − | *Das abgetastete Quellensignal wird mit $q_{\rm A}(t)$ bezeichnet und dessen Spektralfunktion mit $Q_{\rm A}(f)$. Die Abtastung erfolgt stets bei $ν · T_{\rm A}$. | + | *Das abgetastete Quellensignal wird mit $q_{\rm A}(t)$ bezeichnet und dessen Spektralfunktion mit $Q_{\rm A}(f)$. |
| + | * Die Abtastung erfolgt stets bei $ν · T_{\rm A}$. | ||
| Line 36: | Line 42: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Es gelte $T_{\rm R}/T_{\rm A} = 0.5$. Geben Sie hierfür das normierte Spektrum $G_{\rm R}(f)/T_{\rm A}$ an. Welcher Spektralwert tritt bei $f = 0$ auf? | + | {Es gelte $T_{\rm R}/T_{\rm A} = 0.5$. Geben Sie hierfür das normierte Spektrum $G_{\rm R}(f)/T_{\rm A}$ an. Welcher Spektralwert tritt bei $f = 0$ auf? |
|type="{}"} | |type="{}"} | ||
$G_{\rm R}(f=0)/T_{\rm A} \ = \ $ { 0.5 3% } | $G_{\rm R}(f=0)/T_{\rm A} \ = \ $ { 0.5 3% } | ||
| − | {Wie lautet das Spektrum $Q_{\rm A}(f)$ bei natürlicher Abtastung? Vorschläge: | + | {Wie lautet das Spektrum $Q_{\rm A}(f)$ bei natürlicher Abtastung? Vorschläge: |
|type="[]"} | |type="[]"} | ||
- Es gilt $Q_{\rm A}(f) = P_{\rm δ}(f) ∗ Q(f)$. | - Es gilt $Q_{\rm A}(f) = P_{\rm δ}(f) ∗ Q(f)$. | ||
| Line 51: | Line 57: | ||
- Nein. | - Nein. | ||
| − | { Wie lautet das Spektrum $Q_{\rm A}(f)$ bei diskreter Abtastung? Vorschläge: | + | { Wie lautet das Spektrum $Q_{\rm A}(f)$ bei diskreter Abtastung? Vorschläge: |
|type="[]"} | |type="[]"} | ||
- Es gilt $Q_{\rm A}(f) = P_{\rm δ}(f) ∗ Q(f)$. | - Es gilt $Q_{\rm A}(f) = P_{\rm δ}(f) ∗ Q(f)$. | ||
Revision as of 10:02, 1 April 2020
Die ideale Abtastung lässt sich im Zeitbereich durch Multiplikation des analogen Quellensignals $q(t)$ mit einem Diracpuls $p_δ(t)$ beschreiben:
- $$ q_{\rm A}(t) = p_{\delta}(t) \cdot q(t) \hspace{0.05cm}.$$
Diracimpulse – unendlich schmal und unendlich hoch – und dementsprechend auch der Diracpuls $p_δ(t)$ lassen sich in der Praxis jedoch nicht realisieren. Hier muss statt dessen vom Rechteckpuls $p_{\rm R}(t)$ ausgegangen werden, wobei folgender Zusammenhang gilt:
- $$ p_{\rm R}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \right ]\star g_{\rm R}(t)\hspace{0.9cm}\text{mit}\hspace{0.9cm} g_{\rm R}(t) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} < T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} = T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.005cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} > T_{\rm R}/2\hspace{0.05cm}. \\ \end{array}$$
Die Dauer $T_{\rm R}$ eines Rechteckimpulses $g_{\rm R}(t)$ sollte dabei (deutlich) kleiner sein als der Abstand $T_{\rm A}$ zweier Abtastwerte.
In der Grafik ist dieses Verhältnis mit $T_{\rm R}/T_{\rm A} = 0.5$ sehr groß gewählt, um den Unterschied zwischen der „natürlichen Abtastung” und der „diskreten Abtastung” besonders deutlich werden zu lassen:
- Bei natürlicher Abtastung ist das abgetastete Signal $q_{\rm A}(t)$ gleich dem Produkt aus Rechteckpuls $p_{\rm R}(t)$ und analogem Quellensignal $q(t)$:
- $$q_{\rm A}(t) = p_{\rm R}(t) \cdot q(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t)\hspace{0.05cm}.$$
- Dagegen lautet die entsprechende Gleichung für die diskrete Abtastung:
- $$ q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \cdot q(t)\right ]\star g_{\rm R}(t)\hspace{0.05cm}.$$
In der Grafik sind diese Signale in blau (natürliche Abtastung) bzw. grün (diskrete Abtastung) skizziert.
Zur Signalrekonstruktion wird ein rechteckförmiger Tiefpass $H(f)$ mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2$ und der Verstärkung $T_{\rm A}/T_{\rm R}$ im Durchlassbereich eingesetzt:
- $$H(f) = \left\{ \begin{array}{l} T_{\rm A}/T_{\rm R} \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2}\hspace{0.05cm}. \\ \end{array}$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Pulscodemodulation.
- Bezug genommen wird insbesondere auf die Seite Natürliche und diskrete Abtastung.
- Das abgetastete Quellensignal wird mit $q_{\rm A}(t)$ bezeichnet und dessen Spektralfunktion mit $Q_{\rm A}(f)$.
- Die Abtastung erfolgt stets bei $ν · T_{\rm A}$.
Fragebogen
Musterlösung
- $$ G_{\rm R}(f) = T_{\rm R} \cdot {\rm si}(\pi f T_{\rm R}) \hspace{0.3cm} {\rm mit}\hspace{0.3cm} {\rm si}(x) = \sin(x)/x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{G_{\rm R}(f)}{T_{\rm A}} = \frac{T_{\rm R}}{T_{\rm A}} \cdot {\rm si}(\pi f T_{\rm R}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{G_{\rm R}(f = 0)}{T_{\rm A}} =\frac{T_{\rm R}}{T_{\rm A}}\hspace{0.15cm}\underline { = 0.5} \hspace{0.05cm}.$$
(2) Richtig ist der zweite Lösungsvorschlag:
- Aus der angegebenen Gleichung im Zeitbereich ergibt sich mit dem Faltungssatz:
- $$q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}Q_{\rm A}(f) = \left [ \frac{1}{T_{\rm A}}\cdot P_{\rm \delta}(f) \cdot G_{\rm R}(f) \right ] \star Q(f) = \left [ P_{\rm \delta}(f) \cdot \frac{G_{\rm R}(f)}{{T_{\rm A}}} \right ] \star Q(f) \hspace{0.05cm}.$$
- Der erste Lösungsvorschlag gilt nur bei idealer Abtastung (mit einem Diracpuls) und der letzte bei diskreter Abtastung.
(3) Die Antwort ist JA:
- Ausgehend von dem Ergebnis der Teilaufgabe (2) erhält man mit der Spektralfunktion des Diracpulses
- $$Q_{\rm A}(f) = \left [ P_{\rm \delta}(f) \cdot \frac{G_{\rm R}(f)}{{T_{\rm A}}} \right ] \star Q(f)= \left [ \frac{G_{\rm R}(f)}{{T_{\rm A}}} \cdot \sum_{\mu = -\infty}^{+\infty} \delta(f - \mu \cdot f_{\rm A})\right ] \star Q(f) \hspace{0.05cm}.$$
- Ist das Abtasttheorem erfüllt und der Tiefpass richtig dimensioniert, so liegen von den unendlich vielen Faltungsprodukten nur das Faltungsprodukt mit $μ = 0$ im Durchlassbereich.
- Unter Berücksichtigung des Verstärkungsfaktors $T_{\rm A}/T_{\rm R}$ erhält man somit für das Spektrum am Filterausgang:
- $$V(f) = \frac{T_{\rm A}}{T_{\rm R}} \cdot \left [ \frac{G_{\rm R}(f = 0)}{{T_{\rm A}}} \cdot \delta(f )\right ] \star Q(f)= Q(f) \hspace{0.05cm}.$$
(4) Richtig ist der letzte Lösungsvorschlag.
- Verlagert man den Faktor $1/T_{\rm A}$ zum Rechteckimpuls, so erhält man bei diskreter Abtastung mit dem Faltungssatz:
- $$ q_{\rm A}(t) = \big [ p_{\rm \delta}(t)\cdot q(t) \big ] \star \frac{g_{\rm R}(t)}{T_{\rm A}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}Q_{\rm A}(f)= \big [ P_{\rm \delta}(f)\star Q(f) \big ] \cdot \frac{G_{\rm R}(f)}{T_{\rm A}}\hspace{0.05cm}.$$
(5) Die Antwort ist NEIN:
- Die Gewichtungsfunktion $G_{\rm R}(f)$ betrifft nun auch den inneren Kern $(μ = 0)$ des Faltungsproduktes.
- Alle anderen Terme $(μ ≠ 0)$ werden durch den Tiefpass eliminiert. Man erhält hier im relevanten Bereich $|f| < f_{\rm A}/2$:
- $$V(f) = \frac{T_{\rm A}}{T_{\rm R}} \cdot \frac{G_{\rm R}(f )}{{T_{\rm A}}} \cdot Q(f) = 2 \cdot 0.5 \cdot {\rm si}(\pi f T_{\rm R})\cdot Q(f) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}V(f) = Q(f) \cdot {\rm si}(\pi f T_{\rm R})\hspace{0.05cm}.$$
- Sieht man hier keine zusätzliche Entzerrung vor, so werden die höheren Frequenzen entsprechend der si–Funktion gedämpft.
- Die höchste Signalfrequenz $(f = f_{\rm A}/2)$ wird hierbei am stärksten abgesenkt:
- $$V(f = \frac{f_{\rm A}}{2}) = Q( \frac{f_{\rm A}}{2}) \cdot {\rm si}(\pi \cdot \frac{T_{\rm R}}{2 \cdot T_{\rm A}})= Q( \frac{f_{\rm A}}{2}) \cdot {\rm si}(\pi \cdot \frac{\sin(\pi/4)}{\pi/4})\approx 0.9 \cdot Q( \frac{f_{\rm A}}{2}) \hspace{0.05cm}.$$