Difference between revisions of "Aufgaben:Exercise 2.2: Simple Two-Path Channel Model"
| Line 4: | Line 4: | ||
[[File:P_ID2157__Mob_A_2_2.png|right|frame|Zwei äquivalente Modelle <br>für den Zweiwege-Kanal]] | [[File:P_ID2157__Mob_A_2_2.png|right|frame|Zwei äquivalente Modelle <br>für den Zweiwege-Kanal]] | ||
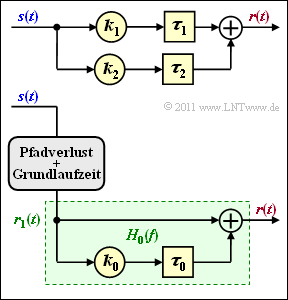
Here we consider a two-way–channel for mobile radio according to the adjacent graphic, characterized by the model parameters | Here we consider a two-way–channel for mobile radio according to the adjacent graphic, characterized by the model parameters | ||
| − | :$$k_1 = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} \ | + | :$$k_1 = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} \tau_{1} = 10\,{\rm µ s}\hspace{0.05cm}, \hspace{0.2cm}\tau_{2} = 11\,{\rm µ s} \hspace{0.05cm}.$$ |
Two different numerical values are considered for the damping factor on the secondary path: | Two different numerical values are considered for the damping factor on the secondary path: | ||
| Line 81: | Line 81: | ||
'''(3)''' The impulse location is | '''(3)''' The impulse location is | ||
| − | $$h_{\rm 0}(\ | + | $$h_{\rm 0}(\tau) = \delta(\tau) + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$ |
By Fourier transformation you get the frequency response | By Fourier transformation you get the frequency response | ||
| − | :$$H_{\rm 0}(f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + k_0 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \ | + | :$$H_{\rm 0}(f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + k_0 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_0}=1 + k_0 \cdot {\cos}( 2 \pi f \tau_0) + {\rm j}\cdot k_0 \cdot {\sin |
}( 2 \pi f \tau_0) | }( 2 \pi f \tau_0) | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Line 110: | Line 110: | ||
'''(5)''' The difference $\tau_{\rm max} \ – \tau_{\rm min}$ of the delay times in the two paths is equal to $\tau_0 = 1 \ \ \rm µ s$. | '''(5)''' The difference $\tau_{\rm max} \ – \tau_{\rm min}$ of the delay times in the two paths is equal to $\tau_0 = 1 \ \ \rm µ s$. | ||
*So the coherence bandwidth | *So the coherence bandwidth | ||
| − | :$$B_{\rm K}\hspace{0.01cm}' = {1}/{\ | + | :$$B_{\rm K}\hspace{0.01cm}' = {1}/{\tau_{\rm 0} \hspace{0.1cm} \underline {=1\,{\rm MHz} \hspace{0.05cm}.$$ |
*The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow k_0 = $1 in the same way. | *The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow k_0 = $1 in the same way. | ||
Revision as of 13:47, 15 April 2020
Here we consider a two-way–channel for mobile radio according to the adjacent graphic, characterized by the model parameters
- $$k_1 = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} \tau_{1} = 10\,{\rm µ s}\hspace{0.05cm}, \hspace{0.2cm}\tau_{2} = 11\,{\rm µ s} \hspace{0.05cm}.$$
Two different numerical values are considered for the damping factor on the secondary path:
- $k_2 = 2 \cdot 10^{-5}$ ⇒ subtasks (1) to (4),
- $k_2 = 10^{-4}$ ⇒ subtasks (5) and (6)'.
An equivalent channel model is shown below, with only the part highlighted in green being considered further. This means:
- The basic attenuation (path loss) and the basic propagation time are not taken into account here.
- The frequency response of this $(k_0, \tau_0$)–model is designated $H_0(f)$ .
An important descriptive parameter of any mobile radio system is the coherence bandwidth $B_{\rm K}$, which is defined in the chapter GWSSUS–Channel Model . With this it can be decided whether the system can be considered as non-frequency selective:
- This is justified if the signal bandwidth $B_{\rm S}$ is significantly smaller than the coherence bandwidth $B_{\rm K}$.
- Otherwise, the mobile radio system is frequency selective, which requires a more complicated description.
As a simple approximation for the coherence bandwidth, the reciprocal value of pulse broadening is often used in the literature (marked by an apostrophe in our learning tutorial):
- $$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\frac_{\rm max} - \frac_{\rm min}} \hspace{0.05cm}.$$
Notes:
- This task belongs to the topic of the chapter Mehrwegeempfang beim Mobilfunk.
- For the solution you also need the speed of light $c = 3 \cdot 10^8 \ \rm m/s$.
- For $k_2$ only positive values are used here You may remember: If the secondary path is created by reflection on a wall, a phase change by $\pi$ is actually to be considered, resulting in a negative $k_2$–value.
Questionnaire
Sample solution
(2) The damping factor is $k_0 = k_2/k_1 \ \ \underline {= 0.2}$ and the delay time $\tau_0 = \tau_2 \ – \tau_1 \ \underline {= 1 \ \ \rm µ s}$.
- The path loss effective for both paths is thus $k_1 = 10^{-4}$ and the basic delay time is $\tau_1 = 10 \ \ \rm µ s$.
(3) The impulse location is $$h_{\rm 0}(\tau) = \delta(\tau) + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$ By Fourier transformation you get the frequency response :$$H_{\rm 0}(f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + k_0 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_0}=1 + k_0 \cdot {\cos}( 2 \pi f \tau_0) + {\rm j}\cdot k_0 \cdot {\sin
}( 2 \pi f \tau_0)
\hspace{0.05cm},$$
and thus to the following magnitude frequency response:
$$|H_{\rm 0}(f)| = \sqrt{ \left [ 1 + k_0 \cdot {\cos}( 2 \pi f \tau_0)\right ]^2 + k_0^2 \cdot {\sin^2 }( 2 \pi f \tau_0)}\hspace{0.3cm}
\Rightarrow \hspace{0.3cm}|H_{\rm 0}(f = 0)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1+ k_0 \hspace{0.1cm} \underline {=1.2} \hspace{0.05cm},$$ $$|H_{\rm 0}(f = 250\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi/2)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi/2)} = \sqrt{1+ k_0^2} \hspace{0.1cm} \underline {\approx 1.02} \hspace{0.05cm},$$ $$|H_{\rm 0}(f = 500\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi)} = {1- k_0} \hspace{0.1cm} \underline {= 0.8} \hspace{0.05cm}.$$ [[File:P_ID2158__Mob_A_2_2c.png|right|frame|Amount frequency response of a two-way channel]] The graphic (red curve) shows the function $|H_0(f)|$. *The values you are looking for are marked by the yellow dots. *The blue curve refers to the subtask (5) with $k_0 = 1 \ \Rightarrow \ k_2 = k_0 \cdot k_1 = 10^{–4}$. '''(4)''' Correct is the <u>solution 1</u>: *Destructive overlays exist for $|H_0(f)| < 1$, for example for $f = 500 \ \rm kHz$. *On the other hand: :$$|H_{\rm 0}(f = 750\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 250\,{\rm kHz})| \approx 1.02 > 1\hspace{0.05cm},$$ :$$|H_{\rm 0}(f = 1\,{\rm MHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 0)| = 1.2 > 1 \hspace{0.05cm}.$ '''(5)''' The difference $\tau_{\rm max} \ – \tau_{\rm min}$ of the delay times in the two paths is equal to $\tau_0 = 1 \ \ \rm µ s$. *So the coherence bandwidth :'"`UNIQ-MathJax34-QINU`"' *The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow k_0 = $1 in the same way. *In the graph this approximation $B_{\rm K}\hspace{0.01cm}'$ is drawn for the coherence bandwidth. '''(6)''' Correct is the <u>solution 2</u>: *The channel is not frequency selective if the coherence bandwidth $B_{\rm K}$ is significantly larger than the signal bandwidth $B_{\rm S}$.
- For the given channel, this is true for GSM, but not for UMTS. For UMTS there is a frequency-selective channel.
{