Difference between revisions of "Applets:Generation of Walsh functions"
(Die Seite wurde neu angelegt: „== program description== <br> This applet allows to display the Hadamard matrices $\mathbf{H}_J$ for the construction of the Walsh functions …“) |
|||
| Line 1: | Line 1: | ||
| − | == | + | {{LntAppletLinkEn|walsh}} |
| + | |||
| + | == Program description== | ||
<br> | <br> | ||
| − | This applet allows to display the Hadamard matrices $\mathbf{H}_J$ for the construction of the Walsh functions $w_j$. The factor $J$ of the band spreading as well as the selection of the individual Walsh functions (by blue bordering the rows of the matrix) can be changed. | + | This applet allows to display the Hadamard matrices $\mathbf{H}_J$ for the construction of the Walsh functions $w_j$. The factor $J$ of the band spreading as well as the selection of the individual Walsh functions (by blue bordering the rows of the matrix) can be changed. |
==Theoretical background== | ==Theoretical background== | ||
| Line 7: | Line 9: | ||
===Application=== | ===Application=== | ||
<br> | <br> | ||
| − | The '''Walsh functions''' are a group of periodic orthogonal functions. Their application in digital signal processing is mainly in the use for band spreading in CDMA systems, for example the mobile radio standard UMTS. | + | The '''Walsh functions''' are a group of periodic orthogonal functions. Their application in digital signal processing is mainly in the use for band spreading in CDMA systems, for example the mobile radio standard UMTS. |
| − | *Due to their orthogonal properties and the favourable | + | *Due to their orthogonal properties and the favourable periodic cross-correlation function $\rm (PCCF)$, the Walsh functions represent optimal spreading sequences for a distortion-free channel and a synchronous CDMA system. If you take any two lines and form the correlation (averaging over the products), the PCCF value is always zero. |
| − | *In asynchronous operation (example: uplink of a mobile radio system) or de-orthogonalization due to multipath propagation, Walsh functions alone are not necessarily suitable for band spreading | + | *In asynchronous operation (example: uplink of a mobile radio system) or de-orthogonalization due to multipath propagation, Walsh functions alone are not necessarily suitable for band spreading. |
| − | *In terms of | + | *In terms of $\rm (PACF)$ (''periodic cross-correlation function'') these sequences are less good: Each individual Walsh function has a different PACF and each individual PACF is less good than a comparable pseudo noise $\rm (PN)$ sequence. That means: The synchronization is more difficult with Walsh functions than with PN sequences. |
| + | <br> | ||
| − | === Construction== | + | === Construction=== |
<br> | <br> | ||
| − | The construction of Walsh functions can be done recursively using the '''Hadamard matrices''. A Hadamard matrix $\mathbf{H}_J$ of order $J$ is a $J\times J$ matrix, which contains line by line the $\pm 1$ weights of the Walsh sequences. The orders of the Hadamard matrices are fixed to powers of two, i.e. $J = 2^G$ applies to a natural number $G$. Starting from $\mathbf{H}_1 = [+1]$ and | + | The construction of Walsh functions can be done recursively using the '''Hadamard matrices'''. |
| + | *A Hadamard matrix $\mathbf{H}_J$ of order $J$ is a $J\times J$ matrix, which contains line by line the $\pm 1$ weights of the Walsh sequences. | ||
| + | *The orders of the Hadamard matrices are fixed to powers of two, i.e. $J = 2^G$ applies to a natural number $G$. Starting from $\mathbf{H}_1 = [+1]$ and | ||
| − | + | :$$ | |
\mathbf{H}_2 = | \mathbf{H}_2 = | ||
\left[ \begin{array}{rr} | \left[ \begin{array}{rr} | ||
+1 & +1\\ | +1 & +1\\ | ||
+1 & -1 \\ | +1 & -1 \\ | ||
| − | \end | + | \end{array}\right] |
| − | + | $$ | |
the following relationship applies to the generation of further Hadamard matrices: | the following relationship applies to the generation of further Hadamard matrices: | ||
| − | + | :$$ | |
\mathbf{H}_{2N} = | \mathbf{H}_{2N} = | ||
\left[ \begin{array}{rr} | \left[ \begin{array}{rr} | ||
| − | +\mathbf{H}_N & +\mathbf{H}_N | + | +\mathbf{H}_N & +\mathbf{H}_N\\ |
| − | +\mathbf{H}_N & -\mathbf{H}_N | + | +\mathbf{H}_N & -\mathbf{H}_N \\ |
| − | \end | + | \end{array}\right] |
| − | + | $$ | |
<br> | <br> | ||
| − | {{ | + | |
| − | $\text{ | + | {{GraueBox|TEXT= |
| − | [[File: | + | $\text{Example:}$ The graphic shows the Hadamard matrix $\mathbf H_8$ (right) and the $J -1$ spreading sequences which can be constructed with it. |
| + | [[File:P_ID1882__Mod_T_5_3_S7_neu.png|right|frame| Walsh spreading sequences $(J = 8)$ and Hadamard matrix $\mathbf H_8$ ]] | ||
*$J - 1$ because the unspread sequence $w_0(t)$ is usually not used. | *$J - 1$ because the unspread sequence $w_0(t)$ is usually not used. | ||
*Please note the color assignment between the lines of the Hadamard matrix and the spreading sequences $w_j(t)$. | *Please note the color assignment between the lines of the Hadamard matrix and the spreading sequences $w_j(t)$. | ||
| Line 40: | Line 46: | ||
<br clear=all> | <br clear=all> | ||
| − | == | + | ==How to use the applet== |
<br> | <br> | ||
| − | [[File:Walsh | + | [[File:Walsh Handhabung.png|right|550px]] |
'''(A)''' Selection of the factor for band spreading as power of two of $G$ | '''(A)''' Selection of the factor for band spreading as power of two of $G$ | ||
| Line 51: | Line 57: | ||
== About the authors== | == About the authors== | ||
| − | |||
| + | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | ||
| + | *Die erste Version wurde 2007 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Thomas_Gro.C3.9Fer_.28Diplomarbeit_LB_2006.2C_danach_freie_Mitarbeit_bis_2010.29|Thomas Großer]] im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). | ||
| + | *2018/2019 wurde das Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] (Ingenieurspraxis, Betreuer: [[Biografien_und_Bibliografien/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]] ) auf „HTML5” umgesetzt und neu gestaltet. | ||
| + | |||
| + | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| + | <br> | ||
| + | {{LntAppletLinkEn|walsh}} | ||
Translated with www.DeepL.com/Translator (free version) | Translated with www.DeepL.com/Translator (free version) | ||
Revision as of 17:51, 12 May 2020
Contents
Program description
This applet allows to display the Hadamard matrices $\mathbf{H}_J$ for the construction of the Walsh functions $w_j$. The factor $J$ of the band spreading as well as the selection of the individual Walsh functions (by blue bordering the rows of the matrix) can be changed.
Theoretical background
Application
The Walsh functions are a group of periodic orthogonal functions. Their application in digital signal processing is mainly in the use for band spreading in CDMA systems, for example the mobile radio standard UMTS.
- Due to their orthogonal properties and the favourable periodic cross-correlation function $\rm (PCCF)$, the Walsh functions represent optimal spreading sequences for a distortion-free channel and a synchronous CDMA system. If you take any two lines and form the correlation (averaging over the products), the PCCF value is always zero.
- In asynchronous operation (example: uplink of a mobile radio system) or de-orthogonalization due to multipath propagation, Walsh functions alone are not necessarily suitable for band spreading.
- In terms of $\rm (PACF)$ (periodic cross-correlation function) these sequences are less good: Each individual Walsh function has a different PACF and each individual PACF is less good than a comparable pseudo noise $\rm (PN)$ sequence. That means: The synchronization is more difficult with Walsh functions than with PN sequences.
Construction
The construction of Walsh functions can be done recursively using the Hadamard matrices.
- A Hadamard matrix $\mathbf{H}_J$ of order $J$ is a $J\times J$ matrix, which contains line by line the $\pm 1$ weights of the Walsh sequences.
- The orders of the Hadamard matrices are fixed to powers of two, i.e. $J = 2^G$ applies to a natural number $G$. Starting from $\mathbf{H}_1 = [+1]$ and
- $$ \mathbf{H}_2 = \left[ \begin{array}{rr} +1 & +1\\ +1 & -1 \\ \end{array}\right] $$
the following relationship applies to the generation of further Hadamard matrices:
- $$ \mathbf{H}_{2N} = \left[ \begin{array}{rr} +\mathbf{H}_N & +\mathbf{H}_N\\ +\mathbf{H}_N & -\mathbf{H}_N \\ \end{array}\right] $$
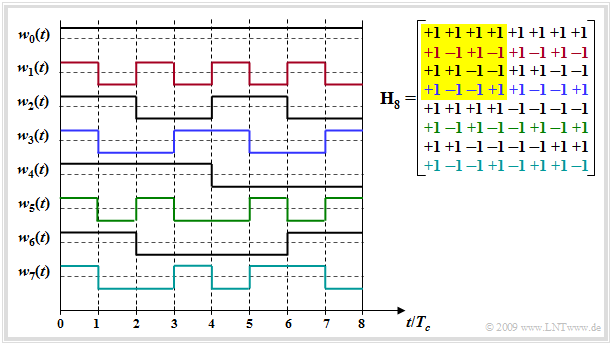
$\text{Example:}$ The graphic shows the Hadamard matrix $\mathbf H_8$ (right) and the $J -1$ spreading sequences which can be constructed with it.
- $J - 1$ because the unspread sequence $w_0(t)$ is usually not used.
- Please note the color assignment between the lines of the Hadamard matrix and the spreading sequences $w_j(t)$.
- The matrix $\mathbf H_4$ is highlighted in yellow.
}
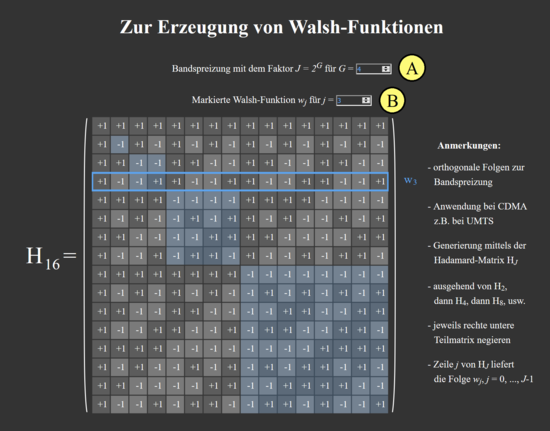
How to use the applet
(A) Selection of the factor for band spreading as power of two of $G$
(B) Selection of the respective Walsh function $w_j$
About the authors
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2007 von Thomas Großer im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018/2019 wurde das Programm von Carolin Mirschina (Ingenieurspraxis, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.
Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
Open Applet in new Tab
Translated with www.DeepL.com/Translator (free version)