Mobile Communications/Distance Dependent Attenuation and Shading

1. Mobile Communications
2. Zeitvariante Übertragungskanäle
3. Distance Dependent Attenuation and Shading

• Previous page
• Next page

• Previous page
• Next page

# ÜBERBLICK ZUM ERSTEN HAUPTKAPITEL #

Das erste Hauptkapitel beschäftigt sich mit zeitvarianten Übertragungskanälen, eine Eigenschaft, die für die mobile Kommunikation von großer Bedeutung ist.  Die Beschreibung erfolgt durchgehend im äquivalenten Tiefpassbereich.

Im Einzelnen werden behandelt:

• die distanzabhängige Dämpfung eines Funksignals und verschiedene Pfadverlustmodelle,
• der durch das  Lognormal–Fading  modellierbare Einfluss von Abschattung  („Shadowing”),
• das nichtfrequenzselektive  Rayleigh–Fading   für Kanäle ohne „Line of Sight  (LoS)”,
• die Berücksichtigung des Dopplereffekts durch das so genannte  Jakes–Spektrum,
• das nichtfrequenzselektive  Rice–Fading   für Kanäle mit Direktpfad  (Line of Sight).

Physikalische Beschreibung des Mobilfunkkanals

Beispiel für ein Mobilfunkszenario

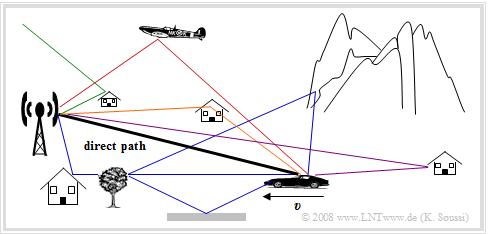
Die Grafik zeigt ein typisches Mobilfunkszenario mit fester Basisstation und einem mobilen Teilnehmer, der sich mit der Geschwindigkeit  $v$  auf die Basisstation zu bewegt.

Bei dieser Darstellung erreicht das Funksignal die Mobilstation über einen direkten Pfad.

Die Antenne des mobilen Teilnehmers empfängt aber auch noch weitere Signalanteile, die auf Umwegen zum Empfänger gelangen, zum Beispiel

• aufgrund von Reflexionen an Häusern,
• einem Gebirge,
• einem Flugzeug,
• der Ionosphäre,
• dem Erdboden.

Anhand dieses Szenarios lassen sich wichtige Probleme bei der Mobilkommunikation erklären:

• Pfadverlust  (englisch:  Path Loss):   Dieser erfasst die Dämpfung der elektromagnetischen Welle, die in starkem Maße von der Entfernung zwischen Sender und Empfänger abhängt.
  

• Abschattung  (englisch:  Shadowing, Long Term Fading):   Diese beschreibt eine langsame Veränderung der Empfangsbedingungen aufgrund der sich ändernden Umgebung, zum Beispiel, wenn man an einem Gebäude vorbeifährt oder wenn man ein Waldstück verlässt.
  

• Mehrwegeausbreitung  (englisch:  Multipath Propagation):   Gelangt das Signal auf mehreren Wegen mit Laufzeitunterschieden zum Empfänger, so kommt es – je nach Signalfrequenz – zu konstruktiven oder destruktiven Überlagerungen bis hin zu völliger Auslöschung.  Für bestimmte Frequenzen ist die Topologie günstig, für andere ungünstig.  Deshalb wird dieser Effekt auch als frequenzselektives Fading  bezeichnet.
  

• Zeitvarianz  (englisch:  Time Variation):   Der Effekt entsteht durch die Bewegung des Senders und/oder des Empfängers, da zu jeder Zeit ein anderer Kanal vorliegt.  Die Übertragungsqualität sinkt rapide, wenn der direkte Pfad durch ein Hindernis abgeschattet ist.  Das Empfangssignal setzt sich dann nur aus den auf Umwegen eintreffenden Teilsignalen zusammen, die aufgrund von Streuungen an Bäumen und Sträuchern sowie eventuell Brechungs– und Beugungserscheinungen gegenüber dem direkten Pfad abgeschwächt sind und sich vektoriell zum Gesamtsignal addieren.
  

• Dopplereffekt  (englisch:  Doppler Spread):   Je nachdem, ob  (und auch in welchem Winkel)  sich die Mobilstation auf den Sender zu bewegt oder sich von diesem entfernt, kommt es zu (leichten) Frequenzverschiebungen und damit zu statistischen Bindungen innerhalb des empfangenen Signals, die  Impulsinterferenzen  bewirken.
  
  

In diesem Kapitel betrachten wir Pfadverlust und Abschattungseffekte genauer.  Die folgenden Kapitel beschäftigen sich mit der Zeitvarianz, auch unter Berücksichtigung des Dopplereffektes.  Das zweite Hauptkapitel beschreibt die Mehrwegeausbreitung, die beim Mobilfunk Echos zur Folge hat.

Freiraumausbreitung

Man spricht von „Freiraumausbreitung”, wenn zwischen Sender und dem im Abstand  $d$  positionierten Empfänger eine Sichtverbindung besteht wie bei der Satellitenkommunikation oder im Weltraum.  Die Radiowellen breiten sich im „leeren Raum” ungehindert kugelförmig um die Sendeantenne aus, werden aber aufgrund des Energieerhaltungssatzes mit zunehmender Entfernung abgeschwächt.

Geometrisch kann man sich das so vorstellen, dass der Radius  $R$  der Kugel und damit auch die Kugelfläche immer größer werden und bei konstanter Gesamtenergie der Energieanteil pro Flächeneinheit proportional zu  $1/R^2$  immer kleiner wird.

Wir gehen von einer unmodulierten Schwingung der Frequenz  $f_{\rm S}$  bzw. der Wellenlänge  $\lambda= c/f_{\rm S}$  aus, wobei  $c = 3 \cdot 10^8\ \rm m/s$  die Lichtgeschwindigkeit  angibt.  Die Signalleistung sei  $P_{\rm S}$.

Harald Friis  hat 1944 eine Gleichung für die Empfangsleistung  $P_{\rm E}(d)$  im Abstand  $d$  angegeben, die allerdings nur im Vakuum gültig ist:

\[P_{\rm E}(d) = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} \cdot \lambda^2}{16 \cdot \pi^2 \cdot d^2 \cdot V_{\rm zus}} = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} /V_{\rm zus}}{K_{\rm FR}(d)} \hspace{0.05cm}.\]

• $G_{\rm S}$  bzw.  $G_{\rm E}$  bezeichnen die Antennengewinne von Sender und Empfänger.
• $V_{\rm zus} > 1$  fasst alle zusätzlichen, von der Wellenausbreitung unabhängigen Verluste zusammen, z. B. durch die Antennen–Kabelzuführungen.
• Die  Freiraumdämpfung  $K_{\rm FR}(d)$  hängt von der Distanz  $d$  ab:

\[K_{\rm FR}(d) = K_{\rm FR}(d_0) \cdot (d/d_0)^2 \hspace{0.2cm}{\rm mit} \hspace{0.2cm} K_{\rm FR}(d_0) = ({4 \pi d_0}/{\lambda} )^2 \hspace{0.05cm}.\]

Meist wird die Freiraumdämpfung logarithmisch mit der Pseudoeinheit „dB” angegeben.  Dann gilt für den Leistungsverlust durch die Freiraumdämpfung („V” steht für „Verlust” in dB):

\[V_{\rm FR}(d) = 10 \cdot {\rm lg} \hspace{0.1cm} K_{\rm FR}(d) = V_{\rm 0} + 20\,\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},\hspace{0.5cm} V_{\rm 0} = V_{\rm FR}(d_0) = 20\,\,{\rm dB} \cdot {\rm lg} \hspace{0.2cm} ({4 \pi d_0}/{\lambda}) \hspace{0.05cm}.\]

Zu dieser Gleichung ist anzumerken:

• Die Gleichung gilt nur im Fernfeld der Antenne  $(d > d_{\rm F})$.  Hierbei ist  $d_{\rm F} = 2 D^2/\lambda$  die so genannte  Fraunhofer–Distanz.  Für  $D$  ist die größte physikalische Abmessung der Sendeantenne einzusetzen.
  

• Die Gleichung gilt nicht für  $d \to 0$.  Hierfür ergäbe sich der Grenzwert  $K_{\rm FR} \to 0$, und es ergäbe sich unabhängig von  $P_{\rm S}$  stets eine unendliche Empfangsleistung  $P_{\rm E}(d \to 0)$.
  

• Die Freiraumdämpfung  $K_{\rm FR}(d)$  nimmt mit zunehmender Entfernung  $d$  quadratisch zu und ebenfalls quadratisch mit zunehmender Signalfrequenz  $f_{\rm S}$, das heißt, mit kleiner werdender Wellenlänge  $\lambda$.
  

• Beispielsweise gilt beim  GSM/E–Netz  $(f_{\rm S} = 1.8 \ \rm GHz$   ⇒   $\lambda \approx 17 \ \rm cm)$:   $K_{\rm FR}(d = 1\ \rm km) = 1.6 \cdot 10^9$.  Beim Empfänger im Abstand von einem Kilometer kommt also nicht mal ein Milliardstel der Sendeleistung an.
  
  

In der  Aufgabe 1.1Z  soll die obige Friis–Gleichung numerisch ausgewertet und interpretiert werden.  Oft setzt man die Freiraumdämpfung in Bezug zu einer geeignet zu definierenden Normierungsdistanz  $d_0$   ⇒   $K_{\rm FR}(d/d_0)$, wobei man häufig  $d_0 = 1\ \rm m$  verwendet.

Gebräuchliches Pfadverlustmodell

Im Gegensatz zu Satelliten– und Richtfunk–Übertragungsstrecken sind beim Landmobilfunk neben der Freiraumdämpfung noch weitere störende Effekte zu berücksichtigen, die ebenfalls zu einer Verminderung der Empfangsleistung beitragen, nämlich:

• Reflexionen:   Durch Überlagerung des Sendesignals mit einer am Erdboden oder an anderen großen glatten Oberflächen reflektierten Signalkomponente können Auslöschungen entstehen, die eine Abnahme der Empfangsleistung bis zur vierten Potenz des Abstandes  $d$  zwischen Sender und Empfänger bewirken.  Mehr hierzu finden Sie in  [Zan05]  und  [PA95].
  

• Beugung:   Hiervon spricht man, wenn das Signal nicht reflektiert, sondern – zum Beispiel an einer Gebäudekante – von seiner Ausbreitungsrichtung abgelenkt wird.  Eine physikalische Erklärung findet man wieder in  [Zan05].
  

• Streuung:   Ist die Verbindung  Sender – Empfänger  durch mehrere Objekte mit unregelmäßiger Oberfläche  (zum Beispiel Bäume oder Sträucher)  unterbrochen, so trifft das Signal am Empfänger in Form vieler Streusignale mit leicht unterschiedlichen Laufzeiten ein.  Die Größe des Hindernisses bestimmt dabei, ob dieses als reflektierendes oder als streuendes Objekt aufzufassen ist.
  
  

Die hier genannten Effekte sind dafür verantwortlich, dass man Mobilfunk auch ohne direkte Sichtverbindung betreiben kann, und damit eine der Grundlagen für den wirtschaftlichen Erfolg der Mobilfunksysteme.  Negativ wirken sich diese Effekte durch eine geringere Empfangsleistung aus, was durch einen größeren Exponenten als  $\gamma = 2$  berücksichtigt werden muss.  Wir sprechen dann nicht mehr von Freiraumdämpfung, sondern allgemein vom  „Pfaddämpfungsfaktor”:

\[K_{\rm P}(d) = K_{\rm P}(d_0) \cdot (d/d_0)^\gamma \hspace{0.05cm}.\]

Die entsprechende dB–Größe nennen wir den  Pfadverlust  $(\rm lg$ ist der Logarithmus zur Basis $10)$:

\[V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},\hspace{0.5cm} V_{\rm 0} = V_{\rm P}(d_0) = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda}\hspace{0.05cm}. \]

Aus diesen Gleichungen ist zu ersehen, dass die Freiraumdämpfung  $V_{\rm FR}(d)$  ein Sonderfall von  $V_{\rm P}(d)$  mit  $\gamma = 2$  ist.  In  [Zan05] werden Zahlenwerte für den Exponenten  $\gamma$  angegeben, die als Mittelwerte über eine Vielzahl von Messungen bestimmt wurden.  Unter anderem gilt

• bei freier Sichtverbindung (Satelliten, Richtfunk):   $\gamma \approx 2$,
  

• in städtischer Umgebung:   $\gamma = 2.7 \ \text{...} \ 3.5$,
  

• in abgeschatteter städtischer Umgebung:   $\gamma = 3.0\ \text{...} \ 5.0$,
  

• innerhalb von Gebäuden ohne Sichtverbindung:   $\gamma = 4.0 \ \text{...} \ 6.0$.
  

Weitere, exaktere Pfadverlustmodelle

Das relativ einfache Pfadverlustmodell entsprechend der letzten Seite ist gut geeignet für Makrozellen, setzt allerdings hohe Antennen der Basisstationen voraus.  Es wurde beispielsweise als Referenz–Szenario bei der Standardisierung von  Long Term Evolution  (LTE) eingesetzt.

Natürlich kann dieses sehr einfache Zweiparameter–Modell  $(V_0, \ \gamma)$  nicht alle Anwendungsfälle mit ausreichender Genauigkeit wiedergeben.  Vielmehr findet man in der Literatur eine Vielzahl weiterer Modelle für die Leistungsdämpfung, die genauer an spezifische Randbedingungen  (Umgebungen)  angepasst sind und auch unterschiedliche Zellgrößen berücksichtigen.  Bekannt sind zum Beispiel – siehe  [Gol06]:

• das  Okumura–Hata–Modell,
  

• das Pfadverlustmodell gemäß  COST 231,
  

• das  Dual–Slope–Modell.
  
  

Dual-Slope-Pfadverlustmodell

$\text{Beispiel 1:}$  Das Dual–Slope–Modell wird oft für Simulationen von Mikrozellen im städtischen Bereich eingesetzt.  Es lautet mit den Kenngrößen  $d_0 = 1\ \rm m$  und  $d_{\rm BP}$  $($Breakpoint, beispielsweise  $d_{\rm BP} = 100\ \rm m)$:

\[V_{\rm P}(d) \hspace{-0.05cm} = \hspace{-0.05cm} V_{\rm 0} \hspace{-0.05cm}+\hspace{-0.05cm} \gamma_0 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 10\,{\rm dB} \hspace{-0.05cm}\cdot \hspace{-0.05cm}{\rm lg} \hspace{0.01cm} \left ( {d}/{d_0} \right ) \hspace{-0.05cm}+ \hspace{-0.05cm}(\gamma_1 \hspace{-0.05cm}- \hspace{-0.05cm}\gamma_0) \hspace{-0.05cm}\cdot \hspace{-0.05cm}10\,{\rm dB} \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm lg} \hspace{0.01cm} \left (1+ {d}/{d_{\rm BP} } \right )\hspace{0.05cm}.\]

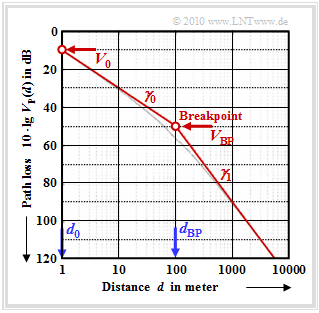
Die Grafik zeigt diesen Verlauf für  $V_{\rm 0} = 10 \ {\rm dB}$,  $\gamma_0 = 2$  und  $\gamma_1 = 4$  im Bereich von einem Meter bis zu mehreren Kilometern  (dünner grauer Kurvenzug).

Häufig wird zur Vereinfachung die in der Grafik rot eingezeichnete asymptotische Näherung

\[V_{\rm P}(d) = \left\{ \begin{array}{c} V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},\\ V_{\rm BP} + \gamma_1 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_{\rm BP})\hspace{0.05cm}, \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm}d < d_{\rm BP}\hspace{0.05cm}, \\ {\rm f\ddot{u}r} \hspace{0.15cm} d \ge d_{\rm BP}\hspace{0.05cm} \\ \end{array}\]

verwendet.  Der Wert  $V_{\rm BP} = 50 \ {\rm dB}$  ergibt sich aus der Gleichung für den ersten Abschnitt an der Grenze  $d = 100\ \rm m$  des Gültigkeitsbereiches.

Hinweis:   In der  Aufgabe 1.1  wird dieses Modell noch eingehend untersucht.

Zusätzlicher Verlust durch Abschattungen (Shadowing)

Der störende Einfluss von Abschattungen wird anhand einer Grafik erläutert, die dem Vorlesungsmanuskript   [Hin08]   entnommen ist:

Pfadverlust ohne und mit Berücksichtigung von Abschattung

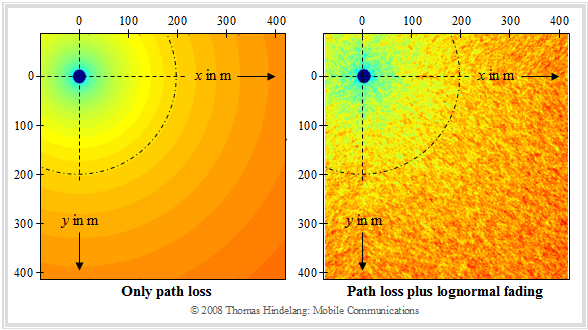
• Die bisherigen Pfadverlustmodelle berücksichtigen jeweils nur die distanzabhängige Signaldämpfung gemäß der linken Grafik und lassen topologische Gegebenheiten wie den Einfluss von Abschattungen außer Acht.

• Im Landmobilfunk führen Abschattungen  (englisch:  Shadowing)  dazu, dass der Signalpegel auch dann variiert, wenn man sich im gleichen Abstand von der Basisstation  (auf einem Kreisbogen)  bewegt.

• Diesen Sachverhalt zeigt die rechte Grafik, wobei dunklere Bereiche einen größeren Pfadverlust kennzeichnen.  Der Unterschied zwischen linkem und rechtem Bild ist auf „Shadowing” zurückzuführen.
  

Die Auswirkungen von Abschattungen  (Shadowing)  lassen sich wie folgt zusammenfassen:

• Bei ruhenden Sender und Empfänger ist die Abschattung deterministisch zu betrachten.  Sie führt dazu, dass der Pfadverlust aufgrund der Abschattung um einen konstanten Wert  $V_{\rm S}$  (in dB) verändert wird:

\[V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)+ V_{\rm S}\hspace{0.05cm}. \]

• Bewegt sich der Empfänger  (oder auch der Sender), so ändert sich der Shadowing–Verlust entsprechend den Koordinaten und demzufolge auch mit der Zeit. Das bedeutet:   $V_{\rm S}$   ⇒   $V_{\rm S}(x, y)$   bzw.   $V_{\rm S}$   ⇒   $V_{\rm S}(t)$.
  

• Allerdings sind solche Kanaländerungen aufgrund von Abschattungen sehr langsam.  Oft bleiben die Bedingungen über mehrere Sekunden gleich und man spricht hier dann von  „Long Term Fading”  im Gegensatz zu schnellem Fading wie  Rayleigh–Fading  und  Rice–Fading.
  

Lognormal–Kanalmodell

Lognormal-WDF   ⇒   Shadowing-Verlust

Zur Berücksichtigung des Verlustes  $V_{\rm S}$  durch Shadowing muss man bei der Systemplanung auf statistische Modelle zurückgreifen, die sich aus empirischen Untersuchungen ergeben haben.

Am bekanntesten ist das  Lognormal–Kanalmodell, das für die Zufallsvariable  $V_{\rm S}$  eine  Gaußsche WDF  zugrundelegt:

\[f_{V_{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm e }^{ - { (V_{\rm S}\hspace{0.05cm}- \hspace{0.05cm}m_{\rm S})^2}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2) } \hspace{0.05cm}.\]

Der Name „Lognormal” ergibt sich aus der Tatsache, dass die dB–Größe  $V_{\rm S}$, die über den Logarithmus aus dem linearen Leistungsdämpfungsfaktor abgeleitet wird, normalverteilt (und damit gaußisch) ist.

Das Lognormal–Kanalmodell ist durch zwei Parameter bestimmt:

• Der Mittelwert  $m_{\rm S} = {\rm E}\big [V_{\rm S}\big ]$  gibt den mittleren Shadowing–Verlust an.  Für ländliches Gebiet wird meist mit  $m_{\rm S} = 6 \ \rm dB$  gerechnet, für städtisches Gebiet geht man von  $14 \ \rm dB$ ... $20 \ \rm dB$  aus.
  

• Auch die Standardabweichung  (oder Streuung)   $\sigma_{\rm S}$  ist für ländliches Gebiet  $(\approx 6 \ \rm dB)$  bzw. für städtische Bedingungen  $($zwischen  $8 \ \rm dB$  und  $12 \ \rm dB)$  unterschiedlich.
  
  

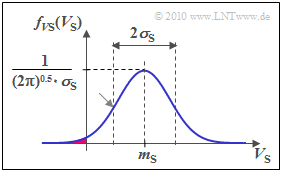
Beachten Sie, dass  $V_{\rm S}$  beim Lognormal–Fading auch negative Werte annehmen kann  (rote Hinterlegung in obiger Grafik), was der Vorstellung von Abschattung eigentlich widerspricht.  In der Praxis hat sich dieses Modell allerdings als sehr gut erwiesen.

Den „Gewinn durch Abschattung” könnte man wie folgt interpretieren:

• In Häuserschluchten kann durch Reflexionen an Gebäuden mehr Energie ankommen, als es nach dem Pfadverlust zu erwarten wäre.
  

• Der Pfadverlustexponent  $\gamma$  wird stets fest vorgegeben, zum Beispiel  $\gamma = 3.76$  im städtischen Gebiet.   Aber es gibt Positionen in der Stadt, bei denen  $\gamma$  kleiner ist.
  

• Ein solch einfaches Modell kann nicht alle Details exakt abbilden.  Man sollte daher nicht versuchen, alle Modelleigenschaften physikalisch zu interpretieren.
  
  

$\text{Fazit:}$  Es ist zweckmäßig, die Pfadverlustanteile in folgender Weise zusammenzufassen:

\[V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t) \hspace{0.25cm}{\rm mit}\hspace{0.25cm} V_{\rm 1} = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)+ m_{\rm S}\hspace{0.05cm}.\]

Der zweite Anteil  $V_{\rm 2}(t)$  beschreibt nun eine Lognormal–WDF mit Mittelwert Null:

\[f_{V_2}(V_2) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S} } \cdot {\rm e }^{ - V_2 ^2/(2 \hspace{0.05cm}\cdot \hspace{0.05cm} \sigma_{\rm S}^2) }\hspace{0.05cm}.\]

Die Entfernungsabhängigkeit von  $V_1$  spielt keine große Rolle und wird hier nicht weiter betrachtet.

Zeitbereichsmodell für das Lognormal–Fading

Pfadverlustmodell mit Lognormal-Fading

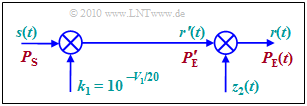
Die Grafik zeigt ein Zeitbereichsmodell, mit dessen Hilfe der Pfadverlust  $V_{\rm P}$  gemäß obiger Gleichung simulativ nachgebildet werden kann.  Hierzu ist anzumerken:

• Das Eingangssignal  $s(t)$  besitze die Leistung  $P_{\rm S}$.  In logarithmischer Darstellung wird die Leistung auf  $1\ \rm mW$  bezogen und es wird die Pseudoeinheit  „dBm”  hinzugefügt.

• Der Pfadverlust  $V_1$  wird durch die Multiplikation mit  $k_1$  erzeugt.  Das Ausgangssignal  $r'(t)$  hat dann eine um  $V_1$  (in dB)  kleinere Leistung:

\[k_1 = 10^{-V_{\rm 1}/20} \hspace{0.1cm} \Rightarrow \hspace{0.1cm} 10 \cdot {\rm lg} \hspace{0.1cm} \frac{P_{\rm E}\hspace{0.05cm}' }{\rm 1\,mW}= 10 \cdot {\rm lg} \hspace{0.1cm} \frac{P_{\rm S} }{\rm 1\,mW} + 20 \cdot {\rm lg} \hspace{0.1cm} k_1 = 10 \cdot {\rm lg} \hspace{0.1cm} \frac{P_{\rm S} }{\rm 1\,mW} - V_1 \hspace{0.05cm}.\]

Zusammenhang zwischen Gauß  $(V_2)$  und Lognormal  $(z_2)$

• Das  (mittelwertfreie)  Lognormal–Fading wird durch Multiplikation mit der Zufallsgröße  $z_2(t)$  nachgebildet. 
• Die WDF ergibt sich aus der Gaußschen Zufallsgröße  $V_2$  durch eine  nichtlineare Transformation  an der Kennlinie 

$$z_2 = g(V_2) = 10^{-V_{\rm 2}/20}.$$

• Für  $z_2< 0$  ist diese WDF gleich Null, und für  $z_2\ge 0$  gilt mit der Abkürzung  $C = \rm ln(10)/20 dB$:

$$f_{z_{\rm 2}}(z_{\rm 2}) = \frac {{\rm e^{- {\rm ln}^2 (z_{\rm 2}) /({2 \hspace{0.05cm}\cdot \hspace{0.05cm} C^2 \hspace{0.05cm} \cdot \hspace{0.05cm} \sigma_{\rm S}^2}) } } }{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.05cm}.$$

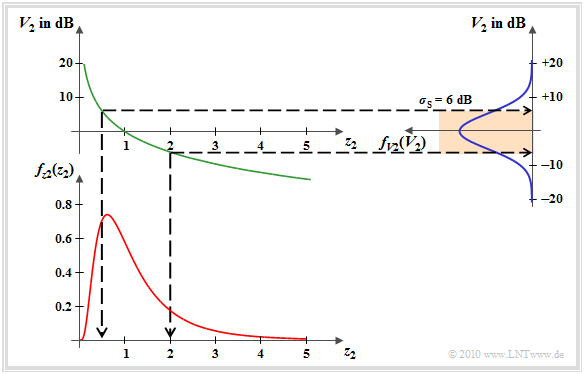
Die Grafik verdeutlicht die Transformation.  Man erkennt

• die Gauß–WDF von  $V_2$  (blau) mit Streuung  $\sigma_{\rm S} = 6 \ \rm dB$,
• die negativ–logarithmische Kennlinie (grün), sowie
• die unsymmetrische WDF (rot) der zu multiplizierenden Größe  $z_2(t)$.

Wir verweisen hier auf die  Aufgabe 1.2Z.

Voraussetzungen für die folgenden Kapitel

Die mittlere Leistung aller am Empfänger ankommenden Signalanteile können mit Hilfe von Pfadverlust– und Abschattungsmodell berechnet werden.

• Das Lognormal–Abschattungsmodell berücksichtigt langsame Änderungen der Reflektoren aufgrund der Topologie, wobei sich die Empfangsbedingungen in Städten nur alle fünf bis zehn Meter ändern und auf dem Land nur alle 30 bis 100 Meter.
• Im Folgenden wird der Pfadverlust und der Einfluss von Abschattungen nicht weiter betrachtet, sondern auf  $1$  normiert.
  

Pfade können sich konstruktiv oder destruktiv überlagern. Die damit zusammenhängenden Änderungen ergeben sich örtlich im Bereich der halben Wellenlänge.  Beim Mobilfunk genügen dabei schon einige wenige Zentimeter, um völlig andere Empfangsbedingungen vorzufinden.  Man spricht von  Fast Fading.  Ein solcher Kanal ist grundsätzlich frequenz– und zeitabhängig.

Für den Rest dieses ersten Hauptkapitel wird die Frequenzabhängigkeit dadurch eliminiert, dass wir von einer einzigen festen Frequenz ausgehen (siehe Grafik).

Signale  $s(t)$  und  $r(t)$  zur Beschreibung des Mobilfunkkanals im Bandpass–Bereich (rot) und im äquivalenten Tiefpassbereich (blau); für die Skizze gilt  $ϕ(t)\equiv 0$

Es gelten somit ab sofort folgende Voraussetzungen:

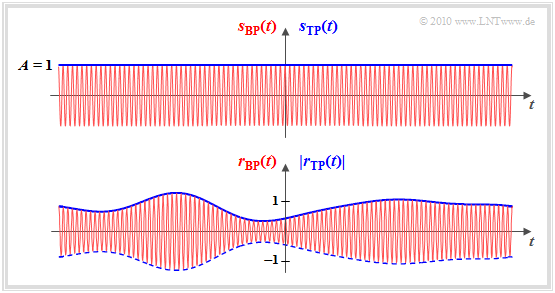
• Das Eingangssignal des Mobilfunkkanals sei eine Cosinusschwingung mit der Amplitude  $A = 1$  und der Frequenz  $f_{\rm T}$.  Wir bezeichnen diese harmonische Schwingung als das  „Sendesignal”  $s_{\rm BP}(t)$.  Dieses Bandpass–Signal ist in der oberen Grafik rot dargestellt.
  

• Das Ausgangssignal  $r_{\rm BP}(t)$  des Mobilfunkkanals – im Folgenden  „Empfangssignal”  genannt – kann sich von  $s_{\rm BP}(t)$  sowohl in der Amplitude  (Hüllkurve)  als auch in der Phase unterscheiden   ⇒   untere Grafik, rot.
  

• Wir betrachten des Weiteren den Mobilfunkkanal meist im  äquivalenten Tiefpassbereich.  Das  „Sendesignal”  ist dann  $s_{\rm TP}(t) = 1$  und somit reell   ⇒   blaue Horizontale in der oberen Grafik.
  

• Das TP–Ausgangssignal  $r_{\rm TP}(t)$  ist im Allgemeinen komplex, wobei die Hüllkurve durch  $a(t)$  gegeben ist und sich die Phase  $\phi(t)$  durch Verschiebungen der Nulldurchgänge bemerkbar macht   ⇒   blaue Hüllkurve in der unteren Grafik.
  
  

$\text{Fazit:}$  Für das  physikalische (Bandpass–)Signal am Ausgang des Mobilfunkkanals  gelte im Folgenden stets:

\[r_{\rm BP}(t) = a(t) \cdot \cos \big [2\pi f_{\rm T} t + \phi(t)\big ]\hspace{0.3cm}\Rightarrow \hspace{0.3cm} a(t) = \vert r_{\rm BP}(t)\vert\hspace{0.05cm}, \hspace{0.2cm} \phi(t) = {\rm arc}\hspace{0.15cm} r_{\rm BP}(t)\hspace{0.05cm}.\]

Aufgaben zum Kapitel

Exercise 1.1: Dual Slope Loss Model

Aufgabe 1.1Z: Einfaches Pfadverlustmodell

Aufgabe 1.2: Lognormal – Kanalmodell

Aufgabe 1.2Z: Nochmals Lognormal–Fading