Difference between revisions of "Aufgaben:Exercise 3.2: GSM Data Rates"
m |
|||
| Line 1: | Line 1: | ||
| − | + | {{{quiz-Header|Book page=Mobile communications/Communities of GSM and UMTS | |
| − | {{quiz-Header| | ||
}} | }} | ||
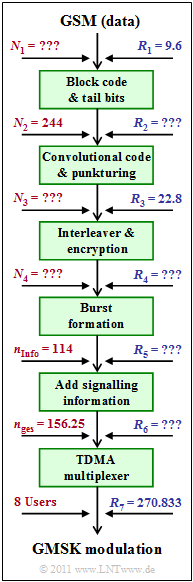
[[File:EN_Mob_A_3_2.png|right|frame|Block diagram of GSM]] | [[File:EN_Mob_A_3_2.png|right|frame|Block diagram of GSM]] | ||
| − | In | + | In this task, the data transmission with GSM is considered. However, since this system was mainly specified for voice transmission, we usually use the duration $T_{\rm R} = 20 \ \rm ms$ of a voice frame as a temporal reference in the following calculations. The input data rate is $R_{1} = 9.6 \ \rm kbit/s$. The number of input bits in each $T_{\rm R}$ frame is $N_{1}$. All parameters labelled "???" in the graphic should be calculated in the task. |
| + | |||
| + | |||
| + | |||
| + | The first blocks you will see in the transmission chain shown: | ||
| + | *the outer coder (block code including four tail bits) with $N_{2} = 244 \ \rm Bit$ per frame $(T_{\rm R} = 20 \ \ \ \rm ms)$ ⇒ Rate $R_{2}$ is to be determined, | ||
| + | *the convolutional coder with the code rate $1/2$, and subsequent puncturing $($waiver of $N_{\rm P} \ \rm bit)$ ⇒ Rate $R_{3} = 22.8 \ \rm kbit/s$, | ||
| + | *Interleaving and encryption, both rate-neutral At the output of this block the rate $R_4$ occurs. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The further signal processing is basically as follows: | |
| − | * | + | *Each $114$ (coded, scrambled, encrypted) data bits are combined together with $34$ control bits (for training sequence, tail bits, guard period) and a pause $($Duration: $8.25 \ \ \rm Bit)$ to a so called ''Normal \ Burst'' . The rate at the output is called $R_{5}$ . |
| − | * | + | *Additionally, further bursts (''Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts'') are added for signalling. The rate after this block is $R_{6}$. |
| − | * | + | *Finally the TDMA multiplexing equipment follows, so that the total gross data rate of the GSM is $R_{\rm ges} = R_{7}$ . |
| − | + | The total gross data rate $R_{\rm ges} = 270,833 \ \rm kbit/s$ (for eight users) is assumed to be known. | |
| Line 26: | Line 29: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The task belongs to the chapter [[Mobile_Kommunikation/Gemeinsamkeiten_von_GSM_und_UMTS|Gemeinsamkeiten von GSM und |
UMTS]]. | UMTS]]. | ||
| − | * | + | *The graphic above summarizes the present description and defines the data rates used. |
| − | * | + | *All rates are given in "$ \rm kbit/s$". |
| − | *$N_{1}, N_{2}, N_{3}$ | + | *$N_{1}, N_{2}, N_{3}$ and $N_{4}$ denote the respective number of bits at the corresponding points of the above block diagram within a time frame of duration $T_{\rm R} = 20 \ \rm ms$. |
| − | *$N_{\rm ges} = 156.25$ | + | *$N_{\rm ges} = 156.25$ is the number of bits after burst formation, related to the duration $T_{\rm Z}$ of a TDMA time slot. Of which $N_{\rm Info} = 114$ are information bits including channel coding. |
| + | |||
| + | |||
| + | |||
| − | === | + | ===Questionnaire== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How many bits are provided by the source in each frame? |
|type="{}"} | |type="{}"} | ||
| − | $N_{1} \ = \ $ { 192 3% } $\ \rm Bit$ | + | $N_{1} \ = \ $ { 192 3% } $\ \ \rm Bit$ |
| − | { | + | {What is the data rate after the outer coder? |
|type="{}"} | |type="{}"} | ||
| − | $R_{2} \ = \ $ { 12.2 3% } $\ \rm kbit/s$ | + | $R_{2} \ = \ $ { 12.2 3% } $\ \ \rm kbit/s$ |
| − | { | + | {How many bits would the convolutional coder deliver alone (without dotting)? |
|type="{}"} | |type="{}"} | ||
| − | $N_{3}\hspace{0.01cm}' \ = \ $ { 488 3% } $\ \rm Bit$ | + | $N_{3}\hspace{0.01cm}' \ = \ $ { 488 3% } $\ \ \rm Bit$ |
| − | { | + | {How many bits does the dotted convolutional coder actually emit? |
|type="{}"} | |type="{}"} | ||
| − | $N_{3} \ = \ $ { 456 3% } $\ \rm Bit$ | + | $N_{3} \ = \ $ { 456 3% } $\ \ \rm Bit$ |
| − | { | + | {What is the data rate after Interleaver and encryption? |
|type="{}"} | |type="{}"} | ||
| − | $R_{4} \ = \ $ { 22.8 3% } $\ \rm kbit/s$ | + | $R_{4} \ = \ $ { 22.8 3% } $\ \ \rm kbit/s$ |
| − | { | + | {How long does a time slot last? |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm Z} \ = \ $ { 576.9 3% } $\ \rm µ s$ | + | $T_{\rm Z} \ = \ $ { 576.9 3% } $\ \ \rm µ s$ |
| − | { | + | {What is the gross data rate for each individual TDMA user? |
|type="{}"} | |type="{}"} | ||
| − | $R_{6} \ = \ $ { 33 | + | $R_{6} \ = \ $ { 33,854 3% } $\ \ \rm kbit/s$ |
| − | { | + | {What gross data rate would be without signaling bits? |
|type="{}"} | |type="{}"} | ||
| − | $R_{5} \ = \ $ { 31.25 3% } $\ \rm kbit/s$ | + | $R_{5} \ = \ $ { 31.25 3% } $\ \ \rm kbit/s$ |
</quiz> | </quiz> | ||
| − | === | + | === sample solution=== |
| − | {{ML | + | {{{ML Kopf} |
| − | '''(1)''' | + | '''(1)''' The following applies $N_{1} = R_{1} \cdot T_{\rm R} = 9.6 {\ \rm kbit/s} \cdot 20 {\ \rm ms} \hspace{0.15cm} \underline{\ 192 \rm bit}$. |
| − | '''(2)''' | + | '''(2)''' Analogous to the subtask '''(1)'' applies: |
| − | + | $$R_2= \frac{N_2}{T_{\rm R}}} = \frac{244\,{\rm bit}}{20\,{\rm ms}}\hspace{0.15cm} \underline { = 12.2\,{\rm kbit/s}}\hspace{0.05cm}.$$ | |
| − | + | Please note: For a redundancy-free binary source (but only this one), there is no difference between "$\rm bit$" and "$\rm bit$". | |
| − | '''(3)''' | + | '''(3)''' The convolutional encoder of rate $1/2$ alone would generate exactly $N_{3}\hspace{0.01cm}' from its $N_{2} = 244$ input bits. \hspace{0.15cm}\underline{= 488}$ generate output bits per frame. |
| − | '''(4)''' | + | '''(4)''' Contrary, $N_{3} follows from the specified data rate $R_{3} = 22.8 \ \rm kbit/s$ \hspace\underline $456. |
| − | * | + | *This means that from $N_{3}' = 488 \ \ \rm Bit$ are removed by the dotting $N_{\rm P} = 32 \ \ \rm Bit$. |
| − | '''(5)''' | + | '''(5)''' Both the interleaving and the encryption are "data neutral" so to speak. Thus the following applies: |
| − | :$$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} | + | :$$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} |
| − | '''(6)''' | + | '''(6)''' The bit duration is $T_{\rm B} = 1/R_{7} = 1/(0.270833 {\ \ \rm Mbit/s}) \approx 3.69 \ \rm µ s$. |
| − | * | + | *A burst - consisting of $156.25 \ \ \rm Bit$ - is transmitted in each time slot of duration $T_{\rm Z}$. |
| − | * | + | *This results in $T_{\rm Z} \hspace{0.15cm}\underline{= 576.9 \ \rm µ s}$. |
| − | '''(7)''' | + | '''(7)''' GSM has eight time slots, with one time slot being periodically assigned to each user. |
| − | * | + | *The gross data rate for each user is $R_{6} = R_{7}/8 \hspace{0.15cm}\underline{ \approx 33.854 \ \rm kbit/s}$. |
| − | '''(8)''' | + | '''(8)''' Considering that for the ''Normal Burst'' the amount of user data (including channel coding) is $114/156.25$, the rate would be without consideration of the added signaling bits: |
| − | :$$R_5 = \frac{n_{\rm ges} } | + | :$$R_5 = \frac{n_{\rm ges} }{\rm Info} \cdot R_4 = \frac{156.25}{114} \cdot 22.8\,{\rm kbit/s}\hspace{0.15cm} \underline { = 31,250\,{\rm kbit/s}}\hspace{0.05cm}.$$ |
| − | * | + | *The same result can be obtained if you consider that in GSM every 13th frame is reserved for ''Common Control'' (signalling info): |
| − | :$$R_5 = \frac{12 }{13 } \cdot 33 | + | :$$R_5 = \frac{12}{13} \cdot 33,854\,{\rm kbit/s} ={ 31,250\,{\rm kbit/s}}\hspace{0.05cm}.$$ |
| − | * | + | *Consequently , the percentage of signaling bits is: |
| − | + | $$\alpha_{\rm SB} = \frac{33.854 - 31.250}{33.854} { \approx 7.7\%}\hspace{0.05cm}.$$ | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 123: | Line 129: | ||
| − | + | Category:Exercises for Mobile Communications|^3.2 Similarities between GSM and UMTS | |
^]] | ^]] | ||
Revision as of 09:39, 25 June 2020
{
- [[{{{Buchseite}}} | Return to book]]
In this task, the data transmission with GSM is considered. However, since this system was mainly specified for voice transmission, we usually use the duration $T_{\rm R} = 20 \ \rm ms$ of a voice frame as a temporal reference in the following calculations. The input data rate is $R_{1} = 9.6 \ \rm kbit/s$. The number of input bits in each $T_{\rm R}$ frame is $N_{1}$. All parameters labelled "???" in the graphic should be calculated in the task.
The first blocks you will see in the transmission chain shown:
- the outer coder (block code including four tail bits) with $N_{2} = 244 \ \rm Bit$ per frame $(T_{\rm R} = 20 \ \ \ \rm ms)$ ⇒ Rate $R_{2}$ is to be determined,
- the convolutional coder with the code rate $1/2$, and subsequent puncturing $($waiver of $N_{\rm P} \ \rm bit)$ ⇒ Rate $R_{3} = 22.8 \ \rm kbit/s$,
- Interleaving and encryption, both rate-neutral At the output of this block the rate $R_4$ occurs.
The further signal processing is basically as follows:
- Each $114$ (coded, scrambled, encrypted) data bits are combined together with $34$ control bits (for training sequence, tail bits, guard period) and a pause $($Duration: $8.25 \ \ \rm Bit)$ to a so called Normal \ Burst . The rate at the output is called $R_{5}$ .
- Additionally, further bursts (Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts) are added for signalling. The rate after this block is $R_{6}$.
- Finally the TDMA multiplexing equipment follows, so that the total gross data rate of the GSM is $R_{\rm ges} = R_{7}$ .
The total gross data rate $R_{\rm ges} = 270,833 \ \rm kbit/s$ (for eight users) is assumed to be known.
Notes:
- The task belongs to the chapter Gemeinsamkeiten von GSM und UMTS.
- The graphic above summarizes the present description and defines the data rates used.
- All rates are given in "$ \rm kbit/s$".
- $N_{1}, N_{2}, N_{3}$ and $N_{4}$ denote the respective number of bits at the corresponding points of the above block diagram within a time frame of duration $T_{\rm R} = 20 \ \rm ms$.
- $N_{\rm ges} = 156.25$ is the number of bits after burst formation, related to the duration $T_{\rm Z}$ of a TDMA time slot. Of which $N_{\rm Info} = 114$ are information bits including channel coding.
=Questionnaire
sample solution
{{{ML Kopf}
(1) The following applies $N_{1} = R_{1} \cdot T_{\rm R} = 9.6 {\ \rm kbit/s} \cdot 20 {\ \rm ms} \hspace{0.15cm} \underline{\ 192 \rm bit}$.
'(2) Analogous to the subtask (1) applies:
$$R_2= \frac{N_2}{T_{\rm R}}} = \frac{244\,{\rm bit}}{20\,{\rm ms}}\hspace{0.15cm} \underline { = 12.2\,{\rm kbit/s}}\hspace{0.05cm}.$$
Please note: For a redundancy-free binary source (but only this one), there is no difference between "$\rm bit$" and "$\rm bit$".
(3) The convolutional encoder of rate $1/2$ alone would generate exactly $N_{3}\hspace{0.01cm}' from its $N_{2} = 244$ input bits. \hspace{0.15cm}\underline{= 488}$ generate output bits per frame.
(4) Contrary, $N_{3} follows from the specified data rate $R_{3} = 22.8 \ \rm kbit/s$ \hspace\underline $456.
- This means that from $N_{3}' = 488 \ \ \rm Bit$ are removed by the dotting $N_{\rm P} = 32 \ \ \rm Bit$.
(5) Both the interleaving and the encryption are "data neutral" so to speak. Thus the following applies:
- $$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} '''(6)''' The bit duration is $T_{\rm B} = 1/R_{7} = 1/(0.270833 {\ \ \rm Mbit/s}) \approx 3.69 \ \rm µ s$. *A burst - consisting of $156.25 \ \ \rm Bit$ - is transmitted in each time slot of duration $T_{\rm Z}$. *This results in $T_{\rm Z} \hspace{0.15cm}\underline{= 576.9 \ \rm µ s}$. '''(7)''' GSM has eight time slots, with one time slot being periodically assigned to each user. *The gross data rate for each user is $R_{6} = R_{7}/8 \hspace{0.15cm}\underline{ \approx 33.854 \ \rm kbit/s}$. '''(8)''' Considering that for the ''Normal Burst'' the amount of user data (including channel coding) is $114/156.25$, the rate would be without consideration of the added signaling bits: :$$R_5 = \frac{n_{\rm ges} }{\rm Info} \cdot R_4 = \frac{156.25}{114} \cdot 22.8\,{\rm kbit/s}\hspace{0.15cm} \underline { = 31,250\,{\rm kbit/s}}\hspace{0.05cm}.$$ *The same result can be obtained if you consider that in GSM every 13th frame is reserved for ''Common Control'' (signalling info): :$$R_5 = \frac{12}{13} \cdot 33,854\,{\rm kbit/s} ={ 31,250\,{\rm kbit/s}}\hspace{0.05cm}.$$ *Consequently , the percentage of signaling bits is: $$\alpha_{\rm SB} = \frac{33.854 - 31.250}{33.854} { \approx 7.7\%}\hspace{0.05cm}.$$
Category:Exercises for Mobile Communications|^3.2 Similarities between GSM and UMTS ^]]