Aufgaben:Exercise 3.2: GSM Data Rates

• Return to book

Block diagram of GSM

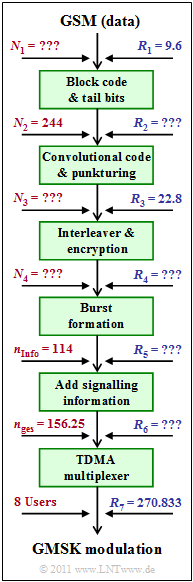
In this task, the data transmission with GSM is considered. However, since this system was mainly specified for voice transmission, we usually use the duration  $T_{\rm R} = 20 \ \rm ms$  of a voice frame as a temporal reference in the following calculations. The input data rate is  $R_{1} = 9.6 \ \rm kbit/s$. The number of input bits in each $T_{\rm R}$ frame is  $N_{1}$. All parameters labelled "???" in the graphic should be calculated in the task.

The first blocks are shown in the transmission chain shown:

• the outer coder (block code including four tail bits) with  $N_{2} = 244 \ \rm Bit$  per frame  $(T_{\rm R} = 20 \ \ \rm ms)$   ⇒   Rate  $R_{2}$  is to be determined,
• the convolutional coder with the code rate  $1/2$, and subsequent puncturing $($waiver of  $N_{\rm P} \ \rm bit)$    ⇒   Rate $R_{3} = 22.8 \ \rm kbit/s$,
• Interleaving and encryption, both rate-neutral At the output of this block the rate  $R_4$  occurs.

The further signal processing is basically as follows:

• Each  $114$  (coded, scrambled, encrypted) data bits are combined together with  $34$  control bits (for training sequence, tail bits, guard period) and a pause $($Duration:   $8.25 \ \ \rm Bit)$  to a so called  Normal \ Burst . The rate at the output is called  $R_{5}$ .
• Additionally, further bursts (Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts) are added for signalling. The rate after this block is  $R_{6}$.
• Finally the TDMA multiplexing equipment follows, so that the total gross data rate of the GSM is  $R_{\rm ges} = R_{7}$ .

The total gross digital data rate  $R_{\rm ges} = 270,833 \ \rm kbit/s$  (for eight users) is assumed to be known.

Notes:

• The task belongs to the chapter  Gemeinsamkeiten von GSM und UMTS.
• The graphic above summarizes the present description and defines the data rates used.
• All rates are given in "$ \rm kbit/s$".
• $N_{1},  N_{2},  N_{3}$  and  $N_{4}$  denote the respective number of bits at the corresponding points of the above block diagram within a time frame of duration  $T_{\rm R} = 20 \ \rm ms$.
• $N_{\rm ges} = 156.25$  is the number of bits after burst formation, related to the duration  $T_{\rm Z}$  of a TDMA time slot. Of which  $N_{\rm Info} = 114$  are information bits including channel coding.

Questionnaire

1

How many bits are provided by the source in each frame?

$N_{1} \ = \ $ $\ \ \rm Bit$

2

What is the data rate after the outer coder?

$R_{2} \ = \ $ $\ \ \rm kbit/s$

3

How many bits would the convolutional coder deliver alone (without dotting)?

$N_{3}\hspace{0.01cm}' \ = \ $ $\ \ \rm Bit$

4

How many bits does the dotted convolutional coder actually emit?

$N_{3} \ = \ $ $\ \ \rm Bit$

5

What is the data rate after Interleaver and encryption?

$R_{4} \ = \ $ $\ \ \rm kbit/s$

6

How long does a time slot last?

$T_{\rm Z} \ = \ $ $\ \ \rm µ s$

7

What is the gross data rate for each individual TDMA user?

$R_{6} \ = \ $ $\ \ \rm kbit/s$

8

What gross data rate would be without signaling bits?

$R_{5} \ = \ $ $\ \ \rm kbit/s$

sample solution

Solution

(1)  The following applies $N_{1} = R_{1} \cdot T_{\rm R} = 9.6 {\ \rm kbit/s} \cdot 20 {\ \rm ms} \hspace{0.15cm} \underline{= 192 \ \rm Bit}$.

(2)  Analogous to subtask (1) applies:

$$R_2= \frac{N_2}{T_{\rm R}} = \frac{244\,{\rm Bit}}{20\,{\rm ms}}\hspace{0.15cm} \underline { = 12.2\,{\rm kbit/s}}\hspace{0.05cm}.$$

Please note:   For a redundancy-free binary source (but only on this one), there is no difference between "$\rm Bit$" and "$\rm bit$".

(3)  Der Faltungscoder der Rate $1/2$ allein würde aus seinen $N_{2} = 244$ Eingangsbits genau $N_{3}\hspace{0.01cm}' \hspace{0.15cm}\underline{= 488}$ Ausgangsbits pro Rahmen generieren.

(4)  Aus der angegebenen Datenrate $R_{3} = 22.8 \ \rm kbit/s$ folgt dagegen $N_{3} \hspace{0.15cm}\underline{= 456}$.

• Das bedeutet, dass von den $N_{3}' = 488 \ \rm Bit$ durch die Punktierung $N_{\rm P} = 32 \ \rm Bit$ entfernt werden.

(5)  Sowohl das Interleaving als auch die Verschlüsselung erfolgt sozusagen „datenneutral”. Damit gilt:

$$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} \Rightarrow N_{4} = N_{3} = 456.$$

(6)  Für die Bitdauer gilt $T_{\rm B} = 1/R_{7} = 1/(0.270833 {\ \rm Mbit/s}) \approx 3.69 \ \rm µ s$.

• In jedem Zeitschlitz der Dauer $T_{\rm Z}$ wird ein Burst – bestehend aus $156.25 \ \rm Bit$ – übertragen.
• Daraus ergibt sich $T_{\rm Z} \hspace{0.15cm}\underline{= 576.9 \ \rm µ s}$.

(7)  Bei GSM gibt es acht Zeitschlitze, wobei jedem Nutzer periodisch ein Zeitschlitz zugewiesen wird.

• Damit beträgt die Bruttodatenrate für jeden Nutzer $R_{6} = R_{7}/8 \hspace{0.15cm}\underline{ \approx 33.854 \ \rm kbit/s}$.

(8)  Berücksichtigt man, dass beim Normal Burst der Anteil der Nutzdaten (inkl. Kanalcodierung) $114/156.25$ beträgt, so wäre die Rate ohne Berücksichtigung der zugefügten Signalisierungsbits:

$$R_5 = \frac{n_{\rm ges} }{n_{\rm Info} } \cdot R_4 = \frac{156.25 }{114} \cdot 22.8\,{\rm kbit/s}\hspace{0.15cm} \underline { = 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$

• Zum gleichen Ergebnis kommt man, wenn man berücksichtigt, dass bei GSM jeder 13. Rahmen für Common Control (Signalisierungs–Info) reserviert ist:

$$R_5 = \frac{12 }{13 } \cdot 33.854\,{\rm kbit/s} ={ 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$

• Damit beträgt der prozentuale Anteil der Signalisierungsbits:

$$\alpha_{\rm SB} = \frac{33.854 - 31.250}{33.854 } { \approx 7.7\%}\hspace{0.05cm}.$$