Difference between revisions of "Aufgaben:Exercise 3.2: GSM Data Rates"
| Line 13: | Line 13: | ||
The further signal processing is basically as follows: | The further signal processing is basically as follows: | ||
| − | *Each $114$ (coded, scrambled, encrypted) data bits are combined together with $34$ control bits (for training sequence, tail bits, guard period) and a pause $($Duration: $8.25 \ \ \rm Bit)$ to a so called ''Normal \ Burst'' . The rate at the output is called $R_{5}$ . | + | *Each $114$ (coded, scrambled, encrypted) data bits are combined together with $34$ control bits (for training sequence, tail bits, guard period) and a pause $($Duration: $8.25 \ \ \rm Bit)$ to a so called ''Normal \ Burst'' . The rate at the output is called $R_{5}$ . |
*Additionally, further bursts (''Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts'') are added for signalling. The rate after this block is $R_{6}$. | *Additionally, further bursts (''Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts'') are added for signalling. The rate after this block is $R_{6}$. | ||
*Finally the TDMA multiplexing equipment follows, so that the total gross data rate of the GSM is $R_{\rm tot} = R_{7}$ . | *Finally the TDMA multiplexing equipment follows, so that the total gross data rate of the GSM is $R_{\rm tot} = R_{7}$ . | ||
Revision as of 20:17, 25 June 2020
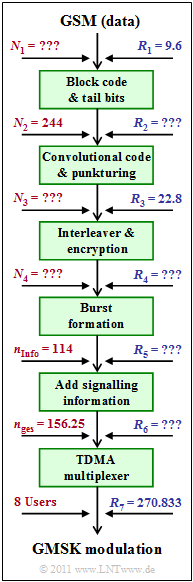
In this task, the data transmission with GSM is considered. However, since this system was mainly specified for voice transmission, we usually use the duration $T_{\rm R} = 20 \ \rm ms$ of a voice frame as a temporal reference in the following calculations. The input data rate is $R_{1} = 9.6 \ \rm kbit/s$. The number of input bits in each $T_{\rm R}$ frame is $N_{1}$. All parameters labelled "???" in the graphic should be calculated in the task.
The first blocks are shown in the transmission chain shown:
- the outer coder (block code including four tail bits) with $N_{2} = 244 \ \rm Bit$ per frame $(T_{\rm R} = 20 \ \ \rm ms)$ ⇒ Rate $R_{2}$ is to be determined,
- the convolutional coder with the code rate $1/2$, and subsequent puncturing $($waiver of $N_{\rm P} \ \rm bit)$ ⇒ Rate $R_{3} = 22.8 \ \rm kbit/s$,
- Interleaving and encryption, both rate-neutral At the output of this block the rate $R_4$ occurs.
The further signal processing is basically as follows:
- Each $114$ (coded, scrambled, encrypted) data bits are combined together with $34$ control bits (for training sequence, tail bits, guard period) and a pause $($Duration: $8.25 \ \ \rm Bit)$ to a so called Normal \ Burst . The rate at the output is called $R_{5}$ .
- Additionally, further bursts (Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts) are added for signalling. The rate after this block is $R_{6}$.
- Finally the TDMA multiplexing equipment follows, so that the total gross data rate of the GSM is $R_{\rm tot} = R_{7}$ .
The total gross digital data rate $R_{\rm tot} = 270,833 \ \rm kbit/s$ (for eight users) is assumed to be known.
Notes:
- The task belongs to the chapter Gemeinsamkeiten von GSM und UMTS.
- The graphic above summarizes the present description and defines the data rates used.
- All rates are given in "$ \rm kbit/s$".
- $N_{1}, N_{2}, N_{3}$ and $N_{4}$ denote the respective number of bits at the corresponding points of the above block diagram within a time frame of duration $T_{\rm R} = 20 \ \rm ms$.
- $N_{\rm tot} = 156.25$ is the number of bits after burst formation, related to the duration $T_{\rm Z}$ of a TDMA time slot. Of which $N_{\rm Info} = 114$ are information bits including channel coding.
Questionnaire
Sample Solution
(1) The following applies $N_{1} = R_{1} \cdot T_{\rm R} = 9.6 {\ \rm kbit/s} \cdot 20 {\ \rm ms} \hspace{0.15cm} \underline{= 192 \ \rm Bit}$.
(2) Analogous to subtask (1) applies:
- $$R_2= \frac{N_2}{T_{\rm R}} = \frac{244\,{\rm Bit}}{20\,{\rm ms}}\hspace{0.15cm} \underline { = 12.2\,{\rm kbit/s}}\hspace{0.05cm}.$$
Please note: For a redundancy-free binary source (but only on this one), there is no difference between "$\rm Bit$" and "$\rm bit$".
(3) The convolutional encoder of rate $1/2$ alone would generate exactly $N_{3}\hspace{0.01cm}' \hspace{0.15cm}\underline{= 488}$ output bits from the input bits $N_{2} = 244$ .
(4) In contrast, $N_{3} \hspace{0.15cm}\underline{= 456}$ is followed by the specifed data rate $R_{3} = 22.8 \ \rm kbit/s$
- This means that from $N_{3}' = 488 \ \rm Bit$ ,$N_{\rm P} = 32 \ \rm Bit$ can be removed by puncturing.
(5) Both the interleaving and the encryption are "data neutral" so to speak. Thus the following applies:
- $$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} \Rightarrow N_{4} = N_{3} = 456.$$
(6) The bit duration is $T_{\rm B} = 1/R_{7} = 1/(0.270833 {\ \rm Mbit/s}) \approx 3.69 \ \rm µ s$.
- In every time slot $T_{\rm Z}$ a Burst of $156.25 \ \rm Bit$ – will be transmitted.
- This makes $T_{\rm Z} \hspace{0.15cm}\underline{= 576.9 \ \rm µ s}$.
(7) GSM has eight time slots, whereby each user is periodically assigned a time slot.
- The gross data rate for each user is $R_{6} = R_{7}/8 \hspace{0.15cm}\underline{ \approx 33.854 \ \rm kbit/s}$.
(8) Considering that in the normal burst the portion of user data (including channel coding) is $114/156.25$, the rate would be without consideration of the added signaling bits:
- $$R_5 = \frac{n_{\rm tot} }{n_{\rm Info} } \cdot R_4 = \frac{156.25}{114} \cdot 22.8\,{\rm kbit/s}\hspace{0.15cm} \underline { = 31,250\,{\rm kbit/s}}\hspace{0.05cm}.$$
- The same result can be obtained if you consider that in GSM every 13th frame is reserved for Common Control (signaling info):
- $$R_5 = \frac{12}{13} \cdot 33,854\,{\rm kbit/s} ={ 31,250\,{\rm kbit/s}}\hspace{0.05cm}.$$
- Thus the percentage of signaling bits is
- $$\alpha_{\rm SB} = \frac{33.854 - 31.250}{33.854 } { \approx 7.7\%}\hspace{0.05cm}.$$