Difference between revisions of "Aufgaben:Exercise 3.7Z: Spread Spectrum in UMTS"
m (Text replacement - "[File:" to "[File:") |
m (Javier moved page Exercises:Exercise 3.7Z: Spread Spectrum in UMTS to Exercise 3.7Z: Spread Spectrum in UMTS: Text replacement - "Exercises:Exercise" to "Aufgaben:Exercise") |
(No difference)
| |
Revision as of 08:42, 30 June 2020
Bei UMTS/CDMA wird die so genannte PN–Modulation angewandt:
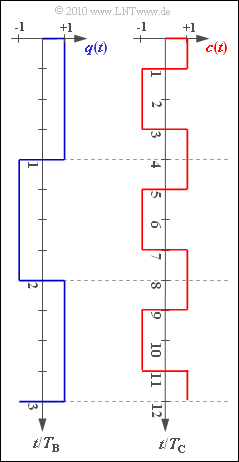
- Das rechteckförmige Digitalsignal $q(t)$ wird dabei mit dem Spreizsignal $c(t)$ multipliziert und ergibt das Sendesignal $s(t)$.
- Dieses ist um den Spreizfaktor $J$ höherfrequenter als $q(t)$; man spricht von Bandspreizung.
Beim Empfänger wird das gleiche Spreizsignal $c(t)$ zugesetzt (und zwar phasensynchron!). Dadurch wird die Bandspreizung rückgängig gemacht ⇒ Bandstauchung.
Die Grafik zeigt beispielhafte Signalverläufe von $q(t)$ und $c(t)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Die Charakteristika von UMTS.
- Bezug genommen wird auch auf das Kapitel Nachrichtentechnische Aspekte von UMTS im Buch „Beispiele von Nachrichtensystemen”.
- Zur Berechnung der Chipdauer $T_{\rm C}$ wird auf die Seite Physikalische Kanäle verwiesen.
- Dort findet man unter anderem die für diese Aufgabe wichtige Information, dass auf dem so genannten Dedicated Physical Channel (DPCH) in zehn Millisekunden genau $15 \cdot 2560 \ \rm Chips$ übertragen werden.
- In Teilaufgabe (5) wird nach Sendechips gefragt. Hierbei bezeichnet beispielsweise das „Sendechip” $s_{3}$ den konstanten Signalwert von $s(t)$ im Zeitintervall $2T_{\rm C}$ ... $3T_{\rm C}$.
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 2:
- Fest vorgegeben ist bei UMTS die Chipdauer $T_{\rm C}$, die in der Teilaufgabe (2) noch berechnet werden soll.
- Je größer der Spreizgrad $J$ ist, desto größer ist die Bitdauer.
(2) Laut dem Hinweis auf der Angabenseite werden in $10 \ \rm ms$ genau $15 \cdot 2560 = 38400 \ \rm Chips$ übertragen.
- Damit beträgt die Chiprate $R_{\rm C} = 100 \cdot 38400 \ {\rm Chips/s} \ \underline{= 3.84 \ \rm Mchip/s}$.
- Die Chipdauer ist der Kehrwert hierzu: $T_{\rm C} \ \underline{\approx 0.26 \ \rm µ s}$.
(3) Jedes Datenbit besteht aus vier Spreizchips ⇒ $\underline{J = 4}$.
(4) Die Bitrate ergibt sich mit dem Spreizfaktor $J = 4$ zu $R_{\rm B} = R_{\rm C}/J \ \underline{= 960 \ \rm kbit/s}$.
- Mit dem für UMTS maximalen Spreizfaktor $J = 512$ beträgt die Bitrate dagegen nur $7.5 \ \rm kbit/s$.
(5) Für das Sendesignal gilt $s(t) = q(t) \cdot c(t)$.
- Die Chips $s_{3}$ und $s_{4}$ des Sendesignals gehören zum ersten Datenbit ($q_{1} = +1)$:
- $$s_3 = c_3 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_4 = c_4 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$
- Dagegen sind die beiden weiteren gesuchten Sendechips dem zweiten Datenbit $(q_{2} = -1)$ zuzuordnen:
- $$s_5 = -c_5= -c_1 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_6 = -c_6= -c_2 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}$$