Aufgaben:Exercise 3.7Z: Spread Spectrum in UMTS

• Return to book

Source signal and spread signal

For UMTS/CDMA, the so-called PN modulation is applied:

• The rectangular digital signal  $q(t)$  is multiplied by the spread signal  $c(t)$  and gives the transmit signal  $s(t)$.
• This is by the spreading factor  $J$  higher frequent (=more frequent) than  $q(t)$; this is called  band spreading.

At the receiver the same spreading signal  $c(t)$  is added (namely in phase!). This reverses the band spreading   ⇒   band compression

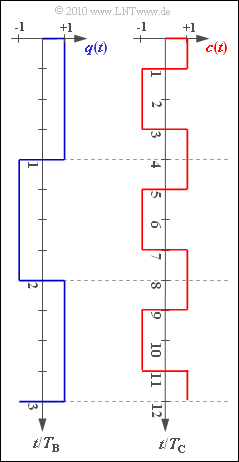
The diagram shows exemplary signal characteristics of  $q(t)$  und  $c(t)$.

Notes:

• This exercise belongs to the chapter   Die Charakteristika von UMTS.
• Reference is made to the chapter  Nachrichtentechnische Aspekte von UMTS  in the book„Beispiele von Nachrichtensystemen”.
• For the calculation of the chip duration   $T_{\rm C}$ , please refer to page  Physikalische Kanäle .
• There you will find, among other things, the information important for this task, which is transmitted on the so-called  Dedicated Physical Channel  (DPCH) in ten milliseconds exactly  $15 \cdot 2560 \ \rm Chips$ .
• In subtask (5), the system asks for transmit chips. For example, the "sending chip"  $s_{3}$  denotes the constant signal value of  $s(t)$  in the time interval  $2T_{\rm C}$ ... $3T_{\rm C}$.

Questionnaire

1

Which of the following statements are true?

	For UMTS the bit duration  $T_{\rm B}$  is fixed.
	For UMTS, the chip duration  $T_{\rm C}$  is fixed.
	Both values depend on the channel conditions.

2

Specify the chip duration  $T_{\rm C}$  and the chip rate  $R_{\rm C}$  in the downlink.

$R_{\rm C} \ = \ $ $\ \rm Mchip/s $

$T_{\rm C} \hspace{0.18cm} = \ $ $ \ \rm µ s $

3

Which spreading factor can be read from the graph on the data page?

$J \ = \ $

4

What is the bit rate with this spreading factor?

$R_{\rm B} \ = \ $ $\ \rm kbit/s $

5

What values do the „chips” of the transmit signal have?

$s_{3} \ = \ $

$s_{4} \ = \ $

$s_{5} \ = \ $

$s_{6} \ = \ $

Musterlösung

Solution

(1)  Richtig ist der Lösungsvorschlag 2:

• Fest vorgegeben ist bei UMTS die Chipdauer $T_{\rm C}$, die in der Teilaufgabe (2) noch berechnet werden soll.
• Je größer der Spreizgrad $J$ ist, desto größer ist die Bitdauer.

(2)  Laut dem Hinweis auf der Angabenseite werden in $10 \ \rm ms$ genau $15 \cdot 2560 = 38400 \ \rm Chips$ übertragen.

• Damit beträgt die Chiprate   $R_{\rm C} = 100 \cdot 38400 \ {\rm Chips/s} \ \underline{= 3.84 \ \rm Mchip/s}$.
• Die Chipdauer ist der Kehrwert hierzu:   $T_{\rm C} \ \underline{\approx 0.26 \ \rm µ s}$.

(3)  Jedes Datenbit besteht aus vier Spreizchips   ⇒   $\underline{J = 4}$.

(4)  Die Bitrate ergibt sich mit dem Spreizfaktor $J = 4$ zu $R_{\rm B} = R_{\rm C}/J \ \underline{= 960 \ \rm kbit/s}$.

• Mit dem für UMTS maximalen Spreizfaktor $J = 512$ beträgt die Bitrate dagegen nur $7.5 \ \rm kbit/s$.

(5)  Für das Sendesignal gilt $s(t) = q(t) \cdot c(t)$.

• Die Chips $s_{3}$ und $s_{4}$ des Sendesignals gehören zum ersten Datenbit ($q_{1} = +1)$:

$$s_3 = c_3 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_4 = c_4 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$

• Dagegen sind die beiden weiteren gesuchten Sendechips dem zweiten Datenbit $(q_{2} = -1)$ zuzuordnen:

$$s_5 = -c_5= -c_1 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_6 = -c_6= -c_2 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}$$