Difference between revisions of "Aufgaben:Exercise 1.1: Music Signals"
From LNTwww
m (Text replacement - "[[Signaldarstellung/" to "[[Signal_Representation/") |
|||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Signaldarstellung/Prinzip der Nachrichtenübertragung}} | {{quiz-Header|Buchseite=Signaldarstellung/Prinzip der Nachrichtenübertragung}} | ||
| − | [[File:P_ID339__Sig_A_1_1.png|right|frame| | + | [[File:P_ID339__Sig_A_1_1.png|right|frame|Music signals, original and <br> noisy and/or distorted?]] |
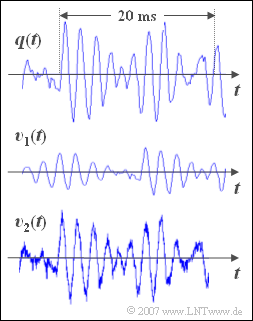
| − | + | On the right you see a ca. $\text{30 ms}$ long section of a music signal <math>q(t)</math>. It is the piece „For Elise” by Ludwig van Beethoven. | |
| − | * | + | *Underneath are drawn two sink signals <math>v_1(t)</math> and <math>v_2(t)</math>, which were recorded after the transmission of the music signal <math>q(t)</math> over two different channels. |
| − | * | + | *The following controls allow you to listen to the first fourteen seconds of each of the three audio signals <math>q(t)</math>, <math>v_1(t)</math> and <math>v_2(t)</math>. |
| Line 24: | Line 24: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The task belongs to chapter [[Signal_Representation/Prinzip_der_Nachrichtenübertragung|Prinzip der Nachrichtenübertragung]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Estimate the signal frequency of <math>q(t)</math> in the displayed section. |
|type="()"} | |type="()"} | ||
| − | - | + | - The signal frequency is approximately <math>f = 250\,\text{Hz}</math>. |
| − | + | + | + The signal frequency is approximately <math>f = 500\,\text{Hz}</math>. |
| − | - | + | - The signal frequency is about <math>f = 1\,\text{kHz}</math>. |
| − | { | + | {Which statements are true for the signal <math>v_1(t)</math> ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The signal <math>v_1(t)</math> is undistorted compared to <math>q(t)</math>. |
| − | - | + | - The signal <math>v_1(t)</math> shows distortions compared to <math>q(t)</math> . |
| − | - | + | - The signal <math>v_1(t)</math> is noisy compared to <math>q(t)</math> . |
| − | { | + | {Which statements are true for the signal <math>v_2(t)</math> ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The signal <math>v_2(t)</math> is undistorted compared to <math>q(t)</math> . |
| − | - | + | - The signal <math>v_2(t)</math> shows distortions compared to <math>q(t)</math> . |
| − | + | + | + The signal <math>v_2(t)</math> is noisy compared to <math>q(t)</math> . |
| − | { | + | {One of the signals is opposite the original <math>q(t)</math> undistorted and not noisy. <br> Estimate the attenuation factor and the running time for this. |
|type="{}"} | |type="{}"} | ||
<math> \alpha \ = \ </math> { 0.2-0.4 } | <math> \alpha \ = \ </math> { 0.2-0.4 } | ||
| Line 59: | Line 59: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solutions=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>solution 2</u>: |
| − | * | + | *In the marked range of $20$ milliseconds approx. $10$ oscillations can be detected. |
| − | * | + | *From this the result follows approximately for the signal frequency; $f = {10}/(20 \,\text{ms}) = 500 \,\text{Hz}$. |
| − | '''(2)''' | + | '''(2)''' Correct is the <u>solution 1</u>: |
| − | * | + | *The signal <math>v_1(t)</math> is undistorted compared to the original signal <math>q(t)</math>. The following applies: $v_1(t)=\alpha \cdot q(t-\tau) .$ |
*Eine Dämpfung <math>\alpha</math> und eine Laufzeit <math>\tau</math> führen nicht zu Verzerrungen, sondern das Signal ist dann nur leiser und es kommt später als das Original. | *Eine Dämpfung <math>\alpha</math> und eine Laufzeit <math>\tau</math> führen nicht zu Verzerrungen, sondern das Signal ist dann nur leiser und es kommt später als das Original. | ||
Revision as of 22:15, 7 August 2020
On the right you see a ca. $\text{30 ms}$ long section of a music signal \(q(t)\). It is the piece „For Elise” by Ludwig van Beethoven.
- Underneath are drawn two sink signals \(v_1(t)\) and \(v_2(t)\), which were recorded after the transmission of the music signal \(q(t)\) over two different channels.
- The following controls allow you to listen to the first fourteen seconds of each of the three audio signals \(q(t)\), \(v_1(t)\) and \(v_2(t)\).
Originalsignal \(q(t)\)
Sinkensignal \(v_1(t)\)
Sinkensignal \(v_2(t)\)
Notes:
- The task belongs to chapter Prinzip der Nachrichtenübertragung.
Questions
Solutions
(1) Correct is the solution 2:
- In the marked range of $20$ milliseconds approx. $10$ oscillations can be detected.
- From this the result follows approximately for the signal frequency; $f = {10}/(20 \,\text{ms}) = 500 \,\text{Hz}$.
(2) Correct is the solution 1:
- The signal \(v_1(t)\) is undistorted compared to the original signal \(q(t)\). The following applies: $v_1(t)=\alpha \cdot q(t-\tau) .$
- Eine Dämpfung \(\alpha\) und eine Laufzeit \(\tau\) führen nicht zu Verzerrungen, sondern das Signal ist dann nur leiser und es kommt später als das Original.
(3) Richtig sind die Lösungsvorschläge 1 und 3:
- Man erkennt sowohl im dargestellten Signalverlauf \(v_2(t)\) als auch im Audiosignal additives Rauschen ⇒ Lösungsvorschlag 3.
- Der Signalrauschabstand beträgt dabei ca. $\text{30 dB}$; dies ist aber aus dieser Darstellung nicht erkennbar.
- Richtig ist aber auch der Lösungsvorschlag 1: Ohne diesen Rauschanteil wäre \(v_2(t)\) identisch mit \(q(t)\).
(4) Das Signal \(v_1(t)\) ist formgleich mit dem Originalsignal \(q(t)\) und unterscheidet sich von diesem lediglich
- durch den Amplitudenfaktor $\alpha = \underline{\text{0.3}}$ (dies entspricht etwa $\text{–10 dB)}$
- und die Laufzeit $\tau = \underline{10\,\text{ms}}$.