Aufgaben:Exercise 1.1: Music Signals

• Return to book

Music signals, original,
noisy and/or distorted?

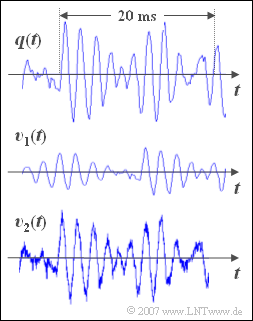
On the right you see a ca.  $\text{30 ms}$  long section of a music signal  [math]\displaystyle{ q(t) }[/math]. It is the piece „For Elise” by Ludwig van Beethoven.

• Underneath are drawn two sink signals  [math]\displaystyle{ v_1(t) }[/math]  and  [math]\displaystyle{ v_2(t) }[/math], which were recorded after the transmission of the music signal  [math]\displaystyle{ q(t) }[/math]  over two different channels.

• The following controls allow you to listen to the first fourteen seconds of each of the three audio signals  [math]\displaystyle{ q(t) }[/math],  [math]\displaystyle{ v_1(t) }[/math]  and  [math]\displaystyle{ v_2(t) }[/math].

Originalsignal  [math]\displaystyle{ q(t) }[/math]

Sinkensignal  [math]\displaystyle{ v_1(t) }[/math]

Sinkensignal  [math]\displaystyle{ v_2(t) }[/math]

Notes:

• The task belongs to chapter  Prinzip der Nachrichtenübertragung.

Questions

1 Estimate the signal frequency of  [math]\displaystyle{ q(t) }[/math]  in the displayed section.

	The signal frequency is approximately  [math]\displaystyle{ f = 250\,\text{Hz} }[/math].
	The signal frequency is approximately  [math]\displaystyle{ f = 500\,\text{Hz} }[/math].
	The signal frequency is about  [math]\displaystyle{ f = 1\,\text{kHz} }[/math].

2 Which statements are true for the signal  [math]\displaystyle{ v_1(t) }[/math] ?

	The signal  [math]\displaystyle{ v_1(t) }[/math]  is undistorted compared to [math]\displaystyle{ q(t) }[/math].
	The signal  [math]\displaystyle{ v_1(t) }[/math]  shows distortions compared to  [math]\displaystyle{ q(t) }[/math] .
	The signal  [math]\displaystyle{ v_1(t) }[/math]  is noisy compared to  [math]\displaystyle{ q(t) }[/math] .

3 Which statements are true for the signal  [math]\displaystyle{ v_2(t) }[/math] ?

	The signal  [math]\displaystyle{ v_2(t) }[/math]  is undistorted compared to  [math]\displaystyle{ q(t) }[/math] .
	The signal  [math]\displaystyle{ v_2(t) }[/math]  shows distortions compared to  [math]\displaystyle{ q(t) }[/math] .
	The signal  [math]\displaystyle{ v_2(t) }[/math]  is noisy compared to  [math]\displaystyle{ q(t) }[/math] .

4 One of the signals is opposite the original  [math]\displaystyle{ q(t) }[/math]  undistorted and not noisy.
Estimate the attenuation factor and the running time for this.

[math]\displaystyle{ \alpha \ = \ }[/math]

[math]\displaystyle{ \tau \ = \ }[/math] $\ \text{ms}$

Solutions

Solution

(1)  Correct is the solution 2:

• In the marked range of $20$ milliseconds approx.   $10$  oscillations can be detected.
• From this the result  follows approximately for the signal frequency; $f = {10}/(20 \,\text{ms}) = 500 \,\text{Hz}$.

(2)  Correct is the solution 1:

• The signal  [math]\displaystyle{ v_1(t) }[/math]  is undistorted compared to the original signal [math]\displaystyle{ q(t) }[/math]. The following applies:   $v_1(t)=\alpha \cdot q(t-\tau) .$

• An attenuation  [math]\displaystyle{ \alpha }[/math]  and a delay  [math]\displaystyle{ \tau }[/math]  do not cause distortion, but the signal is then only quieter and comes later than the original.

(3)  Correct are the solutions 1 and 3:

• One can recognize both in the displayed signal  [math]\displaystyle{ v_2(t) }[/math]  and in the audio signal  additive noise   ⇒   solution 3.
• The signal-to-noise ratio is approx.   $\text{30 dB}$; but this cannot be seen from this representation.
• Correct is also the solution 1:   Without this noise component  [math]\displaystyle{ v_2(t) }[/math]  identical with  [math]\displaystyle{ q(t) }[/math].

(4)  The signal  [math]\displaystyle{ v_1(t) }[/math]  is identical in form to the original signal  [math]\displaystyle{ q(t) }[/math]  and differs from it only

• by the attenuation factor  $\alpha = \underline{\text{0.3}}$  (dies entspricht etwa  $\text{–10 dB)}$
• and the delay  $\tau = \underline{10\,\text{ms}}$.