Difference between revisions of "Aufgaben:Exercise 2.6: Complex Fourier Series"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=*Buch*/*Kapitel* }} ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="[]"} - Falsch + Richtig {Input-Box Frage |…“) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=*Buch*/*Kapitel* | {{quiz-Header|Buchseite=*Buch*/*Kapitel* | ||
}} | }} | ||
| + | |||
| + | [[File:P_ID312__Sig_A_2_6.png|250px|right|Komplexe Fourierreihe (Aufgabe A2.6)]] | ||
| + | |||
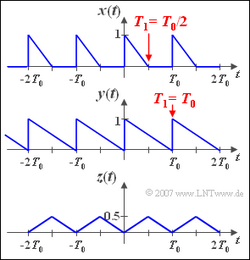
| + | Wir betrachten das Signal $x(t)$, das durch die beiden Parameter $T_0$ und $T_1$ festgelegt ist, wobei stets $T_1 \leq T_0$ gelten soll. Für die komplexen Fourierkoeffizienten | ||
| + | |||
| + | $$D_n=\frac{1}{T_0}\int_0^{T_0}x(t)\cdot\rm e^{-\rm j\it n\omega_0t}\,{\rm d} \it t$$ | ||
| + | |||
| + | dieses Signals erhält man nach mathematischen Umformungen: | ||
| + | |||
| + | $$D_n=\frac{T_0/T_1}{(2\pi n)^2}\bigg(1-{\rm e}^{-{\rm j} 2\pi nT_1/T_0}\bigg)-\frac{\rm j}{2\pi n}.$$ | ||
| + | |||
| + | Der in der Teilaufgabe 3) behandelte Parametersatz (mit $T_1 = T_0/2$) ist als das Signal $x(t)$ dargestellt. Für $T_1 = T_0$ (Teilaufgabe 2) ergibt sich die Funktion $y(t)$. Im letzten Punkt wird das Signal $z(t)$ betrachtet. Die Fourierkoeffizienten von $z(t)$ lauten: | ||
| + | |||
| + | $$A_0=1/4,$$ | ||
| + | |||
| + | $$A_n=\left\{ \begin{array}{cl} {\frac{\displaystyle-2}{\displaystyle(\pi n)^2}} & {\rm f\ddot{u}r\; geradzahliges\; \it n \rm ,} \\ 0 & {\rm f\ddot{u}r\; ungeradzahliges\; \it n,} \end{array}\right. $$ | ||
| + | |||
| + | $$B_n=0\; \;\; \rm{ f\ddot{u}r\; alle\; \it n.}$$ | ||
| + | |||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {Berechnen Sie den Koeffizienten $D_0$ und zeigen Sie, dass dieser stets reell ist. Welcher Wert ergibt sich für $T_1 = T_0/2$, also für das Signal $x(t)$? | ||
| + | |type="{}"} | ||
| + | Signal $x(t)$: $D_0$ = { 0.25 3% } | ||
| + | |||
| + | {Berechnen Sie für den Sonderfall $T_1 = T_0$ entsprechend dem Signal $y(t)$ die komplexen Fourierkoeffizienten $D_n$ für $n \neq 0$. Wie lauten die Koeffizienten $A_n$ und $B_n$, insbesondere für $n = 1$? | ||
| + | |type="{}"} | ||
| + | Signal $y(t)$: $A_1$ = { 0 } | ||
| + | Signal $y(t)$: $B_1$ = { 0.318 3% } | ||
| − | { | + | {Berechnen Sie nun für das Signal $x(t)$ mit $T_1 = T_0/2$ die Koeffizienten $A_n$ und $B_n$ für $n \neq 0$. Welche Werte ergeben sich hier für $A_1$ und $B_1$? |
|type="{}"} | |type="{}"} | ||
| − | + | Signal $x(t)$: $A_1$ = { 0.203 3% } | |
| + | Signal $x(t)$: $B_1$ = { 0.318 3% } | ||
| + | {Welche der folgenden Aussagen treffen bezüglich x(t), y(t) und z(t) zu? | ||
| + | |type="[]"} | ||
| + | - Es gilt $x(t) = y(t) + z(t)$. | ||
| + | + Es gilt $x(t) = y(t) – z(t)$. | ||
| + | - Die Cosinuskoeffizienten $A_n$ von $x(t)$ und $z(t)$ sind identisch. | ||
| + | + Die Koeffizienten $A_n$ von $x(t)$ und $z(t)$ sind betragsgleich. | ||
| + | + Die Sinuskoeffizienten $B_n$ von $y(t)$ und $z(t)$ sind identisch. | ||
</quiz> | </quiz> | ||
| + | |||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Mit dem Eulerschen Satz ist der komplexe Fourierkoeffizient $D_n$ wie folgt darstellbar: |
| + | |||
| + | |||
| + | Mit der für kleine $\alpha$ -Werte gültigen Näherung $\text{sin}(\alpha ) \approx \alpha$ erhält man für den Imaginärteil: | ||
| + | |||
| + | Für den Realteil erhält man mit $\text{cos}(\alpha) \approx 1 – \alpha_2/2$: | ||
| + | |||
| + | Für $T_1 = T_0/2$ folgt daraus der Gleichsignalkoeffizient $D_0 = 0.25$. Mit $T_1 = T_0$ ergibt sich $D_0 = 0.5$. Ein Vergleich mit den Signalen $x(t)$ und $y(t)$ auf der Angabenseite zeigen die Richtigkeit dieser Ergebnisse. | ||
| + | |||
| + | '''2.''' Es wird nun $n \neq 0$ vorausgesetzt. Mit $T_1 = T_0$ erhält man für den Realteil wegen $\text{cos}(2\pi n) = 1$: | ||
| + | |||
| + | Der Imagnärteil lautet: | ||
| + | |||
| + | Wegen $\text{sin}(2\pi n) = 0$ folgt daraus: | ||
| + | |||
| + | Somit ist | ||
| + | |||
| + | Der Koeffizientenvergleich liefert $A_n = 0$ und $B_n = 1/(\pi n)$, Insbesondere sind $A_1 = 0$ und $B1 \approx 0.318$. Wie zu erwarten war, gilt stets $B_{–n} = –B_n$. | ||
| + | |||
| + | '''3.''' Aus der in der Teilaufgabe 1) berechneten allgemeinen Gleichung folgt mit $T_1/T_0 = 1/2$: | ||
| + | |||
| + | Daraus erhält man die Cosinuskoeffizienten | ||
| + | |||
| + | Die Sinuskoeffizienten lauten: | ||
| + | |||
| + | Hierbei ist berücksichtigt, dass für alle ganzzahligen Werte von n die Funktion $\text{sin}(n\pi ) = 0$ ist. Die jeweils ersten reellen Koeffizienten lauten $A_1 = 2/\pi_2 \approx 0.203$ und $B_1 = 1/\pi \approx 0.318$. | ||
| + | |||
| + | '''4.''' Das Signal $x(t)$ ist gleich der Differenz zwischen $y(t)$ und $z(t)$. Da $z(t)$ eine gerade und $y(t)$ eine ungerade Funktion ist, werden die Cosinuskoeffizienten $A_n$ allein durch die Koeffizienten des Signals $z(t)$ bestimmt, allerdings mit negativen Vorzeichen. Die Sinuskoeffizienten $B_n$ stimmen vollständig mit denen von $y(t)$ überein. Der Gleichsignalanteil von $x(t)$ ergibt sich aus der Differenz der beiden Gleichanteile von $y(t)$ und $z(t): A_0 = 0.5 – 0.25 = 0.25$. Richtig sind somit die Lösungsvorschläge 2, 4 und 5. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^2. Periodische Signale^]] | [[Category:Aufgaben zu Signaldarstellung|^2. Periodische Signale^]] | ||
Revision as of 13:57, 11 April 2016
Wir betrachten das Signal $x(t)$, das durch die beiden Parameter $T_0$ und $T_1$ festgelegt ist, wobei stets $T_1 \leq T_0$ gelten soll. Für die komplexen Fourierkoeffizienten
$$D_n=\frac{1}{T_0}\int_0^{T_0}x(t)\cdot\rm e^{-\rm j\it n\omega_0t}\,{\rm d} \it t$$
dieses Signals erhält man nach mathematischen Umformungen:
$$D_n=\frac{T_0/T_1}{(2\pi n)^2}\bigg(1-{\rm e}^{-{\rm j} 2\pi nT_1/T_0}\bigg)-\frac{\rm j}{2\pi n}.$$
Der in der Teilaufgabe 3) behandelte Parametersatz (mit $T_1 = T_0/2$) ist als das Signal $x(t)$ dargestellt. Für $T_1 = T_0$ (Teilaufgabe 2) ergibt sich die Funktion $y(t)$. Im letzten Punkt wird das Signal $z(t)$ betrachtet. Die Fourierkoeffizienten von $z(t)$ lauten:
$$A_0=1/4,$$
$$A_n=\left\{ \begin{array}{cl} {\frac{\displaystyle-2}{\displaystyle(\pi n)^2}} & {\rm f\ddot{u}r\; geradzahliges\; \it n \rm ,} \\ 0 & {\rm f\ddot{u}r\; ungeradzahliges\; \it n,} \end{array}\right. $$
$$B_n=0\; \;\; \rm{ f\ddot{u}r\; alle\; \it n.}$$
Fragebogen
Musterlösung
Mit der für kleine $\alpha$ -Werte gültigen Näherung $\text{sin}(\alpha ) \approx \alpha$ erhält man für den Imaginärteil:
Für den Realteil erhält man mit $\text{cos}(\alpha) \approx 1 – \alpha_2/2$:
Für $T_1 = T_0/2$ folgt daraus der Gleichsignalkoeffizient $D_0 = 0.25$. Mit $T_1 = T_0$ ergibt sich $D_0 = 0.5$. Ein Vergleich mit den Signalen $x(t)$ und $y(t)$ auf der Angabenseite zeigen die Richtigkeit dieser Ergebnisse.
2. Es wird nun $n \neq 0$ vorausgesetzt. Mit $T_1 = T_0$ erhält man für den Realteil wegen $\text{cos}(2\pi n) = 1$:
Der Imagnärteil lautet:
Wegen $\text{sin}(2\pi n) = 0$ folgt daraus:
Somit ist
Der Koeffizientenvergleich liefert $A_n = 0$ und $B_n = 1/(\pi n)$, Insbesondere sind $A_1 = 0$ und $B1 \approx 0.318$. Wie zu erwarten war, gilt stets $B_{–n} = –B_n$.
3. Aus der in der Teilaufgabe 1) berechneten allgemeinen Gleichung folgt mit $T_1/T_0 = 1/2$:
Daraus erhält man die Cosinuskoeffizienten
Die Sinuskoeffizienten lauten:
Hierbei ist berücksichtigt, dass für alle ganzzahligen Werte von n die Funktion $\text{sin}(n\pi ) = 0$ ist. Die jeweils ersten reellen Koeffizienten lauten $A_1 = 2/\pi_2 \approx 0.203$ und $B_1 = 1/\pi \approx 0.318$.
4. Das Signal $x(t)$ ist gleich der Differenz zwischen $y(t)$ und $z(t)$. Da $z(t)$ eine gerade und $y(t)$ eine ungerade Funktion ist, werden die Cosinuskoeffizienten $A_n$ allein durch die Koeffizienten des Signals $z(t)$ bestimmt, allerdings mit negativen Vorzeichen. Die Sinuskoeffizienten $B_n$ stimmen vollständig mit denen von $y(t)$ überein. Der Gleichsignalanteil von $x(t)$ ergibt sich aus der Differenz der beiden Gleichanteile von $y(t)$ und $z(t): A_0 = 0.5 – 0.25 = 0.25$. Richtig sind somit die Lösungsvorschläge 2, 4 und 5.