Difference between revisions of "Signal Representation/Fourier Series"
| Line 100: | Line 100: | ||
:$$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$ | :$$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$ | ||
| − | + | The last integral is equal to zero due to orthogonality; the first one is zero too (integral over one period). | |
| − | * | + | *Only the middle term contributes here to $A_1$, namely $2 - 0.6 - 0.5 = 0.6. $ |
| − | * | + | *For all further ($n \ge 2$) cosine coefficients all three integrals return the value zero, and thus $A_{n \hspace{0.05cm}\neq \hspace{0.05cm}1}=0$. |
| − | + | To determine the sine coefficients $B_n$ with the determining equation: | |
:$$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$ | :$$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$ | ||
| − | * | + | *For $n \hspace{0.05cm}\neq \hspace{0.05cm}3$ all three integral values are zero and therefore $B_{n \hspace{0.05cm}\neq \hspace{0.05cm}3} = 0.$ |
| − | * | + | *On the other hand, for $n=3$ the last integral provides a contribution, and one gets for the sine coefficient $B_3 = -0.3.$}} |
==Exploitation of Symmetries== | ==Exploitation of Symmetries== | ||
<br> | <br> | ||
| − | + | Some insights into the Fourier coefficients $A_n$ and $B_n$ can already be read from the ''Symmetry properties'' of the time function $x(t)$ . | |
| − | * | + | *If the time signal $x(t)$ is an even function ⇒ axis-symmetrical around the ordinate $(t = 0)$, all sine coefficients $B_n$ disappear, since the sine function itself is an odd function ⇒ $\sin(-\alpha) = -\sin(\alpha)$: |
:$$B_n = 0 \hspace{0.4cm}(n = 1, \ 2, \ 3, \text{...}).$$ | :$$B_n = 0 \hspace{0.4cm}(n = 1, \ 2, \ 3, \text{...}).$$ | ||
| − | * | + | *An odd function $x(t)$ is point symmetric around the coordinate origin $(t= 0; \ x =0)$. Therefore, all cosine coefficients $(A_n = 0)$ disappear here, since the cosine function itself is even. In this case, the constant component $A_0$ is also always zero. |
:$$A_n = 0 \hspace{0.4cm}(n = 0, \ 1, \ 2, \ 3, \text{...}).$$ | :$$A_n = 0 \hspace{0.4cm}(n = 0, \ 1, \ 2, \ 3, \text{...}).$$ | ||
| − | * | + | *If a function without a constant component is present $(A_0 = 0)$ and if this function is odd within a period ⇒ it is $x(t) = -x(t - T_0/2)$, then only odd multiples of the fundamental frequency are present in the Fourier series representation. For the coefficients with an even index, however, the following always applies: |
:$$A_n = B_n = 0 \hspace{0.4cm}(n = 2, \ 4, \ 6, \text{...}).$$ | :$$A_n = B_n = 0 \hspace{0.4cm}(n = 2, \ 4, \ 6, \text{...}).$$ | ||
| − | * | + | *If all coefficients $A_n$ and $B_n$ with even-numbered index $(n = 2, \ 4, \ 6, \text{...})$ equals zero and the coefficient $A_0 \neq 0$, then the symmetry property mentioned in the last point refers to the DC component and applies: |
:$$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$ | :$$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$ | ||
| − | '' | + | ''Remark'': Several of the named symmetry properties can be fulfilled at the same time. |
| − | + | The symmetry properties of the Fourier coefficients are explained in the first part of the german learning video | |
| − | [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)| | + | [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Properties and Accuracy of the fourier series]] . |
| − | [[File:EN_Sig_T_2_4_S3.png|right|frame| | + | [[File:EN_Sig_T_2_4_S3.png|right|frame|Symmetry Properties of the Fourier Coefficients]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ |
| − | + | The above mentioned properties are now illustrated by three signal characteristics. | |
| − | *$x_1(t)$ | + | *$x_1(t)$ is an averaged function ⇒ $A_0 \ne 0$ and is also even, which is accordingly exclusively determined by cosine coefficients $A_n$ $(B_n = 0)$. |
| − | * | + | *In contrast, the odd function $x_2(t)$ all $A_n, \ ( n \ge 0)$ are identical to zero. |
| − | * | + | *Also the odd function $x_3(t)$ contains only sine coefficients, but because of $x_3(t) = -x_3(t - T_0/2)$ exclusively for odd values of $n$.}} |
==Complex Fourier Series== | ==Complex Fourier Series== | ||
<br> | <br> | ||
| − | + | As shown on the page [[ Signal_Representation/Harmonic_Oscillation#Darstellung_mit_Cosinus-_und_Sinusanteil|3 Representation with Cosine and Sine Components]] in case of a harmonic oscillation any periodic signal | |
| + | |||
:$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$ | :$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$ | ||
| − | + | can also be displayed using the magnitude and phase coefficients: | |
:$$x(t) =C_0+\sum^{\infty}_{n=1}C_{\it n} \cdot\cos(n \omega_0 t-\varphi_n).$$ | :$$x(t) =C_0+\sum^{\infty}_{n=1}C_{\it n} \cdot\cos(n \omega_0 t-\varphi_n).$$ | ||
| − | + | These modified Fourier coefficients have the following properties: | |
| − | * | + | *The '''DC coefficient''' $C_0$ is identical with $A_0$. |
| − | * | + | *The '''magnitude coefficient''' read with $n\ge 1$: $C_n = \sqrt{A_n^2 + B_n^2}$. |
| − | * | + | *For the '''phase coefficien''' applies: $\varphi_n = \arctan \hspace{0.05cm}(B_n/A_n$). |
| − | + | With the „Eulerian relationship” $\cos(x) + {\rm j} \cdot \sin(x) = {\rm e}^{{\rm j} \hspace{0.05cm}x}$ we get a second representation variant of the Fourier series evolution, which starts from the complex exponential function. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The '''complex Fourier series''' of a periodic signal x(t) is as follows | |
:$$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$ | :$$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$ | ||
| − | + | Here $D_n$ denote the '''complex Fourier coefficients''', which | |
| − | * | + | *from the cosine coefficients $A_n$ and the sine coefficients $B_n$, or |
| − | * | + | *from the magnitude coefficients $C_n$ and the phase coefficients $\varphi_n$ |
| − | + | can be calculated as follows $($valid for $n \neq 0)$: | |
:$$D_n = 1/2\cdot (A_n - {\rm j}\cdot B_n) =1/2\cdot C_n\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \varphi_n }$$}} | :$$D_n = 1/2\cdot (A_n - {\rm j}\cdot B_n) =1/2\cdot C_n\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \varphi_n }$$}} | ||
| − | + | The complex Fourier coefficients can also be calculated directly using the following equation | |
:$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$ | :$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$ | ||
| − | + | As long as the integration interval $T_0$ is preserved, it can be shifted randomly as with the coefficients $A_n$ and $B_n$ for example from $t = 0$ to $t = T_0$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Conclusion:}$ | + | $\text{Conclusion:}$ The coefficient $D_0 = A_0$ is always real. For the complex coefficients with negative iterating index $(n < 0)$ applies: |
:$$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$}} | :$$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$}} | ||
| Line 199: | Line 200: | ||
==Periodic Signal Spectrum== | ==Periodic Signal Spectrum== | ||
<br> | <br> | ||
| − | + | Starting from the complex Fourier series just derived | |
:$$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$ | :$$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$ | ||
| − | + | and the [[Signal_Representation/Fourier_Transform_Laws#Verschiebungssatz|Displacement Theorem]] (for the frequency domain) one gets the following spectrum for the periodic signal $x(t)$: | |
:$$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$ | :$$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$ | ||
| − | + | This means: | |
*Das Spektrum eines mit $T_0$ periodischen Signals ist ein '''Linienspektrum''' bei ganzzahligen Vielfachen der Grundfrequenz $f_0 = 1/T_0$. | *Das Spektrum eines mit $T_0$ periodischen Signals ist ein '''Linienspektrum''' bei ganzzahligen Vielfachen der Grundfrequenz $f_0 = 1/T_0$. | ||
*Der '''Gleichanteil''' liefert eine Diracfunktion bei $f=0$ mit dem Impulsgewicht $A_0$. | *Der '''Gleichanteil''' liefert eine Diracfunktion bei $f=0$ mit dem Impulsgewicht $A_0$. | ||
| Line 217: | Line 218: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ |
Wir betrachten – wie im [[Signal_Representation/Fourier_Series#Allgemeine_Beschreibung|$\text{Beispiel 1}$]] zu Beginn dieses Abschnitts - zwei periodische Rechtecksignale, jeweils mit Periodendauer $T_0$ und Grundfrequenz $f_0=1/T_0$. | Wir betrachten – wie im [[Signal_Representation/Fourier_Series#Allgemeine_Beschreibung|$\text{Beispiel 1}$]] zu Beginn dieses Abschnitts - zwei periodische Rechtecksignale, jeweils mit Periodendauer $T_0$ und Grundfrequenz $f_0=1/T_0$. | ||
Das obere Signal | Das obere Signal | ||
| Line 231: | Line 232: | ||
| − | [[File:P_ID528__Sig_T_2_4_S6_neu.png|center|frame| | + | [[File:P_ID528__Sig_T_2_4_S6_neu.png|center|frame|Spectrum of a periodic rectangle pulse]] |
| − | + | The function $x_{\rm u}(t)$ shown below is odd: | |
:$$x_{\rm u}(t)={4}/{\pi} \cdot \big[\sin(\omega_0 t)+{1}/{3} \cdot \sin(3\omega_0 t)+{1}/{5} \cdot \sin(5\omega_0 t)+ \, \text{...}\big].$$ | :$$x_{\rm u}(t)={4}/{\pi} \cdot \big[\sin(\omega_0 t)+{1}/{3} \cdot \sin(3\omega_0 t)+{1}/{5} \cdot \sin(5\omega_0 t)+ \, \text{...}\big].$$ | ||
| Line 264: | Line 265: | ||
| − | [[File:P_ID2720__Sig_T_2_4_S7_neu.png|center|frame| | + | [[File:P_ID2720__Sig_T_2_4_S7_neu.png|center|frame|On the Gibbs Phenomenon]] |
| − | + | From the right graphic you can see that the flank and the inner area are marked with | |
| − | $N = 100$ | + | $N = 100$ but due to the Gibbs phenomenon there are still oscillations around $9\%$ at the jumping point. |
| − | * | + | *Since the jump amplitudes here are equal to $2$ the maximum values are approximately $1.18$. |
| − | * | + | *With $N = 1000$ the oscillations would be exactly the same size, but limited to a narrower space and possibly not recognizable with time-discrete representation.}} |
Revision as of 10:27, 27 October 2020
Contents
General Description
Every periodic function $x(t)$ can be fragmented into a trigonometric series, which is called Fourier series, in all areas, where it is continuous or has only finite discontinuities.
$\text{Definition:}$ The Fourier series of a periodic signal $x(t)$ is defined as follows
- $$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t).$$
Here the symbols denote the following definitions:
- $A_0$ the constant component of $x(t)$,
- $A_n$ the cosine coefficients with $n \ge 1$,
- $B_n$ the sine coefficients mit $n \ge 1$,
- $\omega_0 = 2\pi/T_0$ the angular frequency of the periodic signal $(T_0$ is the period duration$)$.
If the Fourier series is to exactly match the actual periodic signal $x(t)$ , an infinite number of cosine and sine coefficients must generally be used for calculation.
- If the Fourier series is interrupted and only $N$ of $A_n$ and $B_n$ coefficients is used, then a slightly different plot of the function results except for some special cases:
- $$x_ N(t) =A_0+\sum^N_{n=1}A_ n \cdot \cos(n \omega_0 t)+\sum^N_{n=1} B_{n} \cdot \sin(n \omega_0 t).$$
- The relation between the periodic signal $x(t)$ and the Fourier series approximation $x_N(t)$ holds:
- $$x(t)=\lim_{N\to \infty} x_{N}(t).$$
- If $N \cdot f_0$ is the highest frequency occurring in the signal $x(t)$ then of course $x_N(t) = x(t)$.
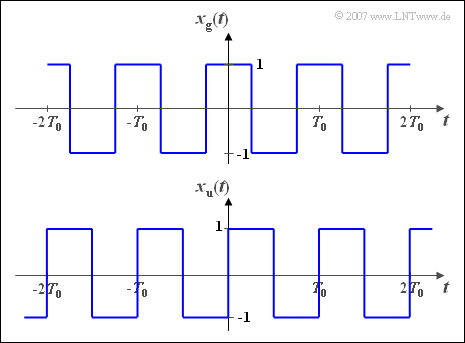
$\text{Example 1:}$ We consider two periodic square wave signals, each with the period duration $T_0$ and the fundamental frequency $\omega_0 = 2\pi/T_0$.
- For the even time signal sketched above: $x_{\rm g}(-t) = x_{\rm g}(t)$.
- The function shown below is odd: $x_{\rm u}(-t) = -x_{\rm u}(t)$.
One finds the fourier series representations of both signals in formularies:
- $$x_{\rm g}(t)=\frac{4}{\pi}\left [ \cos(\omega_0 t)-\frac{1}{3}\cdot \cos(3 \omega_0 t)+\frac{1}{5}\cdot\cos(5 \omega_0 t)- \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm}\right ],$$
- $$x_{\rm u}(t)=\frac{4}{\pi}\left [ \sin(\omega_0 t)+\frac{1}{3}\cdot\sin(3 \omega_0 t)+\frac{1}{5}\cdot\sin(5 \omega_0 t)+ \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm} \right ].$$
- Because of the generally valid relationship
- $$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\, {-}\, \hspace{0.05cm}\text{...}\hspace{0.05cm} \, {+} \hspace{0.05cm}\text{...}\hspace{0.05cm}=\frac{\pi}{4}$$
the amplitudes (maximum values) of the two rectangle pulses result to $1$.
- This can also be verified using the signal curves in the above graphic:
- $$x_{\rm g}(t = 0) = x_{\rm u}(t = T_0/4) = 1.$$
Calculation of the Fourier Coefficients
The Fourier coefficient $A_0$ specifies the constant component which can be determined by averaging over the signal course $x(t)$ . Due to the periodicity, averaging over one period is sufficient:
- $$A_0=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\,{\rm d}t.$$
The integration limits can also be selected from $t = 0$ to $t = T_0$ (or over a differently defined period of equal length).
The determination of the Fourier coefficients $A_n$ and $B_n$ $(n \ge 1)$ is based on the property that the harmonic cosine functions and sine functions are so-called orthogonal functions . For them the following applies:
- $$\int^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\cos(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad if \it \quad m=n,\atop \rm sonst} \right.$$
- $$\int ^{+T_0/2}_{-T_0/2}\sin(n\omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad if \it \quad m=n,\atop \rm sonst} \right.$$
- $$\int ^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=0 \quad \rm f\ddot{u}r\quad alle \ \it m, \ n.$$
$\text{Conclusion:}$ Considering these equations, the cosine coefficients $A_n$ and the sine coefficients $B_n$ result as follows
- $$A_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\cos(n \omega_0 t)\,{\rm d}t,$$
- $$B_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\sin(n \omega_0 t)\,{\rm d}t.$$
The german learning video Calculating the Fourier Coefficients illustrates these equations.
$\text{Example 2:}$ We consider the drawn periodic time function
- $$x(t)=0.4+0.6\cdot \cos(\omega_0 t)-0.3\cdot\sin(3 \omega_0 t).$$
Since the integral of the cosine and sine functions is identical to zero over one period in each case, one obtains for the DC signal coefficient $A_0 = 0.4$.
One determines the cosine coefficient $A_1$ with the following equations $($Integration limits from $t = 0$ to $t = T_0)$:
- $$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$
The last integral is equal to zero due to orthogonality; the first one is zero too (integral over one period).
- Only the middle term contributes here to $A_1$, namely $2 - 0.6 - 0.5 = 0.6. $
- For all further ($n \ge 2$) cosine coefficients all three integrals return the value zero, and thus $A_{n \hspace{0.05cm}\neq \hspace{0.05cm}1}=0$.
To determine the sine coefficients $B_n$ with the determining equation:
- $$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$
- For $n \hspace{0.05cm}\neq \hspace{0.05cm}3$ all three integral values are zero and therefore $B_{n \hspace{0.05cm}\neq \hspace{0.05cm}3} = 0.$
- On the other hand, for $n=3$ the last integral provides a contribution, and one gets for the sine coefficient $B_3 = -0.3.$
Exploitation of Symmetries
Some insights into the Fourier coefficients $A_n$ and $B_n$ can already be read from the Symmetry properties of the time function $x(t)$ .
- If the time signal $x(t)$ is an even function ⇒ axis-symmetrical around the ordinate $(t = 0)$, all sine coefficients $B_n$ disappear, since the sine function itself is an odd function ⇒ $\sin(-\alpha) = -\sin(\alpha)$:
- $$B_n = 0 \hspace{0.4cm}(n = 1, \ 2, \ 3, \text{...}).$$
- An odd function $x(t)$ is point symmetric around the coordinate origin $(t= 0; \ x =0)$. Therefore, all cosine coefficients $(A_n = 0)$ disappear here, since the cosine function itself is even. In this case, the constant component $A_0$ is also always zero.
- $$A_n = 0 \hspace{0.4cm}(n = 0, \ 1, \ 2, \ 3, \text{...}).$$
- If a function without a constant component is present $(A_0 = 0)$ and if this function is odd within a period ⇒ it is $x(t) = -x(t - T_0/2)$, then only odd multiples of the fundamental frequency are present in the Fourier series representation. For the coefficients with an even index, however, the following always applies:
- $$A_n = B_n = 0 \hspace{0.4cm}(n = 2, \ 4, \ 6, \text{...}).$$
- If all coefficients $A_n$ and $B_n$ with even-numbered index $(n = 2, \ 4, \ 6, \text{...})$ equals zero and the coefficient $A_0 \neq 0$, then the symmetry property mentioned in the last point refers to the DC component and applies:
- $$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$
Remark: Several of the named symmetry properties can be fulfilled at the same time.
The symmetry properties of the Fourier coefficients are explained in the first part of the german learning video Properties and Accuracy of the fourier series .
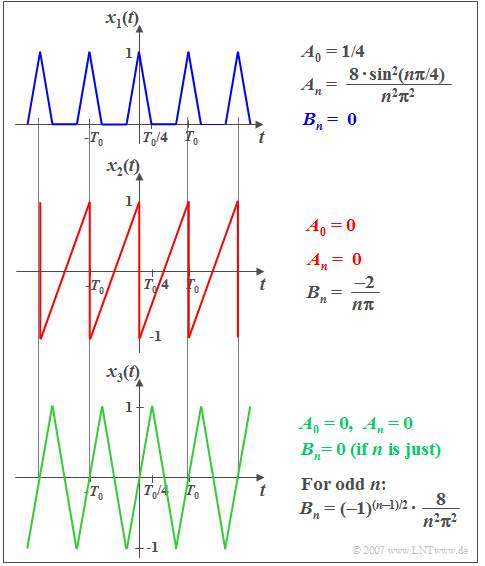
$\text{Example 3:}$ The above mentioned properties are now illustrated by three signal characteristics.
- $x_1(t)$ is an averaged function ⇒ $A_0 \ne 0$ and is also even, which is accordingly exclusively determined by cosine coefficients $A_n$ $(B_n = 0)$.
- In contrast, the odd function $x_2(t)$ all $A_n, \ ( n \ge 0)$ are identical to zero.
- Also the odd function $x_3(t)$ contains only sine coefficients, but because of $x_3(t) = -x_3(t - T_0/2)$ exclusively for odd values of $n$.
Complex Fourier Series
As shown on the page 3 Representation with Cosine and Sine Components in case of a harmonic oscillation any periodic signal
- $$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$
can also be displayed using the magnitude and phase coefficients:
- $$x(t) =C_0+\sum^{\infty}_{n=1}C_{\it n} \cdot\cos(n \omega_0 t-\varphi_n).$$
These modified Fourier coefficients have the following properties:
- The DC coefficient $C_0$ is identical with $A_0$.
- The magnitude coefficient read with $n\ge 1$: $C_n = \sqrt{A_n^2 + B_n^2}$.
- For the phase coefficien applies: $\varphi_n = \arctan \hspace{0.05cm}(B_n/A_n$).
With the „Eulerian relationship” $\cos(x) + {\rm j} \cdot \sin(x) = {\rm e}^{{\rm j} \hspace{0.05cm}x}$ we get a second representation variant of the Fourier series evolution, which starts from the complex exponential function.
$\text{Definition:}$ The complex Fourier series of a periodic signal x(t) is as follows
- $$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$
Here $D_n$ denote the complex Fourier coefficients, which
- from the cosine coefficients $A_n$ and the sine coefficients $B_n$, or
- from the magnitude coefficients $C_n$ and the phase coefficients $\varphi_n$
can be calculated as follows $($valid for $n \neq 0)$:
- $$D_n = 1/2\cdot (A_n - {\rm j}\cdot B_n) =1/2\cdot C_n\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \varphi_n }$$
The complex Fourier coefficients can also be calculated directly using the following equation
- $$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$
As long as the integration interval $T_0$ is preserved, it can be shifted randomly as with the coefficients $A_n$ and $B_n$ for example from $t = 0$ to $t = T_0$.
$\text{Conclusion:}$ The coefficient $D_0 = A_0$ is always real. For the complex coefficients with negative iterating index $(n < 0)$ applies:
- $$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$
Periodic Signal Spectrum
Starting from the complex Fourier series just derived
- $$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$
and the Displacement Theorem (for the frequency domain) one gets the following spectrum for the periodic signal $x(t)$:
- $$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$
This means:
- Das Spektrum eines mit $T_0$ periodischen Signals ist ein Linienspektrum bei ganzzahligen Vielfachen der Grundfrequenz $f_0 = 1/T_0$.
- Der Gleichanteil liefert eine Diracfunktion bei $f=0$ mit dem Impulsgewicht $A_0$.
- Daneben gibt es Diracfunktionen $\delta(f \pm n \cdot f_0)$ bei Vielfachen von $f_0$, wobei $\delta(f - n \cdot f_0)$ eine Diracfunktion bei $f= n \cdot f_0$ (also im positiven Frequenzbereich) und $\delta(f + n \cdot f_0)$ eine solche bei der Frequenz $f= -n \cdot f_0$ (im negativen Frequenzbereich) kennzeichnet.
- Die Impulsgewichte sind im allgemeinen komplex.
Diese Aussagen werden nun anhand zweier Beispiele verdeutlicht.
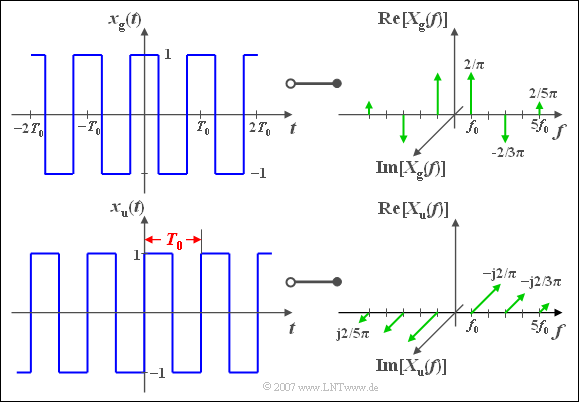
$\text{Example 4:}$ Wir betrachten – wie im $\text{Beispiel 1}$ zu Beginn dieses Abschnitts - zwei periodische Rechtecksignale, jeweils mit Periodendauer $T_0$ und Grundfrequenz $f_0=1/T_0$. Das obere Signal
- $$x_{\rm g}(t)={4}/{\pi} \cdot \big[\cos(\omega_0 t) - {1}/{3} \cdot \cos(3\omega_0 t)+{1}/{5}\cdot \cos(5\omega_0 t) - \, \text{...} \, + \, \text{...} \big]$$
ist eine gerade, aus verschiedenen Cosinusanteilen zusammengesetzte Funktion. Die zugehörige Spektralfunktion $X_{\rm g}(f)$ ist damit rein reell.
Begründung: Wie auf der Seite Spektraldarstellung eines Cosinussignals bereits beschrieben wurde, liefert die Grundwelle zwei Diracfunktionen bei $\pm f_0$, jeweils gewichtet mit $2/\pi$.
- Dieses Gewicht entspricht den (im Allgemeinen komplexen) Fourierkoeffizienten $D_1 = D_{ - 1}^\ast$, die nur im Sonderfall einer geraden Funktion reell sind.
- Weitere Diracfunktionen gibt es bei $\pm 3f_0$ (negativ), $\pm 5f_0$ (positiv), $\pm 7f_0$ (negativ) usw.
- Alle Phasenwerte $\varphi_n$ sind aufgrund der alternierenden Vorzeichen entweder Null oder $\pi$.
The function $x_{\rm u}(t)$ shown below is odd:
- $$x_{\rm u}(t)={4}/{\pi} \cdot \big[\sin(\omega_0 t)+{1}/{3} \cdot \sin(3\omega_0 t)+{1}/{5} \cdot \sin(5\omega_0 t)+ \, \text{...}\big].$$
Begründung: Wie im $\text{Beispiel 4}$ auf der Seite Allgemeine Spektraldarstellung bereits beschrieben wurde, liefert hier die Grundwelle zwei Diracfunktionen bei $+f_0$ $($gewichtet mit $-\text{j}\cdot 2/\pi)$ bzw. bei $-f_0$ $($gewichtet mit $+\text{j}\cdot 2/\pi)$.
- Auch alle weiteren Diracfunktionen bei $\pm 3f_0$, $\pm 5f_0$, usw. sind rein imaginär und liegen in gleicher Richtung wie die Diracs bei $\pm f_0$.
- Die beiden Betragsspektren sind gleich: $\vert X_{\rm u}(f)\vert = \vert X_{\rm g}(f) \vert$.
The Gibbs Phenomenon
Nicht jedes Signal eignet sich für die Fourierreihendarstellung. Hier einige Einschränkungen:
- Eine wichtige Voraussetzung für die Konvergenz der Fourierreihe ist, dass das Signal nur endlich viele Unstetigkeitsstellen je Periode besitzen darf.
- An denjenigen Stellen $t=t_i$, an denen $x(t)$ Sprünge aufweist, konvergiert die Reihe gegen den aus dem jeweiligen links– und rechtsseitigen Grenzwert gebildeten arithmetischen Mittelwert.
- In der Umgebung solcher Sprungstellen kommt es in der Reihendarstellung meist zu hochfrequenten Oszillationen. Dieser Fehler ist von prinzipieller Art, das heißt, er ließe sich auch nicht vermeiden, wenn man unendlich viele Summanden berücksichtigen würde. Man spricht vom Gibbschen Phänomen, benannt nach dem Physiker Josiah Willard Gibbs.
- Durch eine Erhöhung von $N$ wird zwar der fehlerhafte Bereich kleiner, nicht jedoch die maximale Abweichung zwischen $x(t)$ und der Fourierreihendarstellung $x_N(t)$. Der maximale Fehler beträgt ca. $9\%$ der Sprungamplitude – und zwar unabhängig von $N$.
Das Gibbsche Phänomen und weitere interessante Aspekte zu vergleichbaren Effekten werden im Lernvideo
Eigenschaften der Fourierreihendarstellung behandelt.
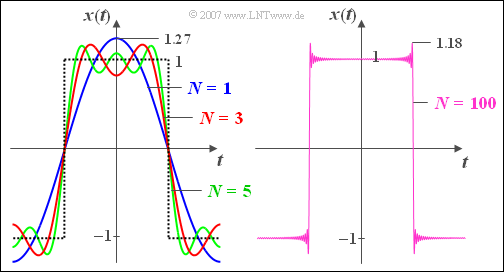
$\text{Example 5:}$ In der linken Grafik sehen Sie gepunktet einen Ausschnitt eines periodischen $\pm 1$–Rechtecksignals und die dazugehörige Fourierreihendarstellung mit $N = 1$ (blau), $N = 3$ (rot) und $N = 5$ (grün) Summanden.
- Die Grundwelle hat hier den Amplitudenwert $4/\pi \approx 1.27$.
- Auch mit $N = 5$ (das bedeutet wegen $A_2 = A_4 = 0$ drei „relevante” Summanden) unterscheidet sich die Fourierreihe vom anzunähernden Rechtecksignal noch deutlich, vor allem im Bereich der Flanke.
From the right graphic you can see that the flank and the inner area are marked with $N = 100$ but due to the Gibbs phenomenon there are still oscillations around $9\%$ at the jumping point.
- Since the jump amplitudes here are equal to $2$ the maximum values are approximately $1.18$.
- With $N = 1000$ the oscillations would be exactly the same size, but limited to a narrower space and possibly not recognizable with time-discrete representation.
Exercises for the Chapter
Aufgabe 2.4: Gleichgerichteter Cosinus
Aufgabe 2.5: Einweggleichrichtung
Aufgabe 2.6: Komplexe Fourierreihe
Aufgabe 2.6Z: Betrag und Phase