Aufgaben:Exercise 4.1Z: High-Pass System

• Return to book

Beispiele für Tiefpass und Hochpass

Die auf der Seite  Eigenschaften von Bandpass-Signalen  dargestellten Beziehungen gelten nicht nur für Signale und Spektren, sondern in gleicher Weise auch für

• den Frequenzgang  $H(f)$  und
• die Impulsantwort  $h(t)$

eines LZI-Systems. Auch diese stehen über die  Fouriertransformation  im Zusammenhang. Nähere Informationen hierzu finden Sie im Buch  Lineare zeitinvariante Systeme.

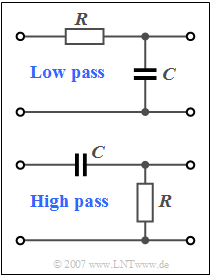
Die Schaltung gemäß der oberen Grafik ist die einfachste Realisierung eines Tiefpasses:

• Für sehr hohe Frequenzen wirkt die Kapazität  $C$  als Kurzschluss, so dass hochfrequente Anteile im Ausgangssignal nicht mehr enthalten sind.
• Dagegen werden niederfrequente Signalanteile durch den Spannungsteiler nur unmerklich abgeschwächt.
• Mit der 3dB–Grenzfrequenz  $f_{\rm G}$  gilt für den Frequenzgang:

$$H_{\rm TP}(f) = \frac{1}{1 + {\rm j} \cdot f / f_{\rm G}} = |H_{\rm TP}(f)|\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_{\rm TP}(f)} .$$

Im zweiten Gleichungsteil ist der Frequenzgang  $H_{\rm TP}(f)$  nach Betrag und Phase aufgespalten.

Die Impulsantwort  $h_{\rm TP}(t)$  erhält man durch Fouriertransformation von  $H_{\rm TP}(f)$, wobei die Zeitkonstante  $\tau = R \cdot C = {1}/({2\pi \cdot f_{\rm G}})$  zu setzen ist.

Für  $t < 0$  ist die Impulsantwort identisch Null, für positive Zeiten gilt:

$$h_{\rm TP}(t) = \frac{1}{\tau} \cdot {\rm e}^{-t / \tau} .$$

Die unten dargestellte Schaltung beschreibt einen Hochpass, dessen Frequenzgang  $H_{\rm HP}(f)$  und Impulsantwort  $h_{\rm HP}(t)$  in dieser Aufgabe ermittelt werden sollen. Ein solcher Hochpass kann auch als Grenzfall eines Bandpasses interpretiert werden.

Hinweis:

• Die Aufgabe gehört zum Kapitel  Unterschiede und Gemeinsamkeiten von Tiefpass- und Bandpass-Signalen.

Fragebogen

1

Welche der folgenden Aussagen sind beim TP-System zutreffend?

	Der Gleichsignalübertragungsfaktor beträgt  $H_{\rm TP}(f = 0) = 2$.
	$|H_{\rm TP}(f)|$  ist bei  $f = f_{\rm G}$  um  $\sqrt{2}$  kleiner als bei  $f = 0$.
	Die Phasenfunktion lautet:   $\varphi_{\rm TP}(f) = \arctan(f/f_{\rm G})$.

2

Begründen Sie, warum stets  $H_{\rm HP}(f) = 1 - H_{\rm TP}(f)$  gelten muss. Berechnen Sie  $H_{\rm HP}(f)$, insbesondere den Wert bei  $f = 0$.

$H_{\rm HP}(f = 0)\ = \ $

3

Welche der folgenden Aussagen sind zutreffend?

	Es gilt  $|H_{\rm HP}(f = f_{\rm G})| = 1 - |H_{\rm TP}(f = f_{\rm G})|$.
	Es gilt  $|H_{\rm HP}(f = f_{\rm G})| = |H_{\rm TP}(f = f_{\rm G})|$.
	Für positive Frequenzen gilt:   $\varphi_{\rm HP}(f) = \varphi_{\rm TP}(f) - \pi/2$.

4

Berechnen Sie die Impulsantwort  $h_{\rm TP}(t)$. Interpretieren Sie das Ergebnis. Welche der folgenden Aussagen sind richtig?

	Es gilt  $h_{\rm HP}(t) = \tau/t \cdot {\rm e}^{-t/\tau}$.
	Es gilt  $h_{\rm HP}(t) = \delta (t) - 1/\tau \cdot {\rm e}^{-t/\tau}$.
	Zum Zeitpunkt  $t = 0$  ist die Impulsantwort unendlich groß.
	Zum Zeitpunkt  $t = \tau$  ist die Impulsantwort gleich ${\rm e}/\tau$.

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 2 und 3:

• Der Gleichsignalübertragungsfaktor ist  $H_{\rm TP}(f = 0) = 1$.
• Für den Betragsfrequenzgang gilt:

$$|H_{\rm TP}(f)| = \frac{1}{\sqrt{1 + ( f / f_{\rm G})^2}} .$$

• Somit ist der Wert bei  $f_{\rm G}$ gleich $\sqrt{1/2}$. Die Leistungsübertragungsfunktion  $|H_{\rm TP}(f)|^2$  ist daher bei  $f = f_{\rm G}$  nur halb so groß als bei  $f = 0$, worauf die Bezeichnung „3dB–Grenzfrequenz” für  $f_{\rm G}$  zurückzuführen ist.
• Die Phasenfunktion wird allgemein nach folgender Gleichung berechnet:

$$\varphi_{\rm TP}(f) = -\arctan\frac{{\rm Im}\left[H_{\rm TP}(f)\right]}{{\rm Re}\left[H_{\rm TP}(f)\right]} .$$

• Mit der konjugiert–komplexen Erweiterung erhält man:

$$H_{\rm TP}(f) = \frac{1}{1 - ( f / f_{\rm G})^2} - \frac{{\rm j} \cdot f / f_{\rm G}}{1 - ( f / f_{\rm G})^2}.$$

• Setzt man dieses Ergebnis in obige Gleichung ein, so ergibt sich:

$$\varphi_{\rm TP}(f) = \arctan\left(f / f_{\rm G}\right) .$$

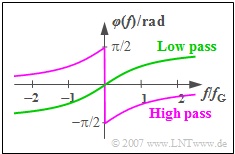
• Der Verlauf ist ausgehend von  $0$  $($bei  $f = 0)$  über  $\pi/2$  $($bei  $f = f_{\rm G})$  bis zu  $\pi$  $($bei  $f \rightarrow \infty)$  monoton steigend.

(2)  Auf der Seite Eigenschaften von Bandpass-Signalen wurde gezeigt, dass ein jedes Bandpass–Signal als Differenz zweier Tiefpass–Signale dargestellt werden kann.

Tiefpass– und Hochpass–Spektrum

Gleiches gilt für Frequenzgänge:

$$H_{\rm BP}(f) = H_1(f) - H_2(f).$$

• Setzt man  $H_2(f) = H_{\rm TP}(f)$  und betrachtet  $H_1(f) = 1$  als Grenzfall einer Tiefpassfunktion mit unendlich großer Bandbreite, so ergibt sich:

$$H_{\rm HP}(f) = 1 - H_{\rm TP}(f).$$

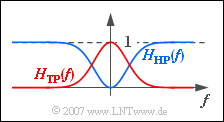
• Wie die Grafik zeigt, ist das Ergebnis wegen  $H_1(f) = 1$  nun ein Hochpass. Mit der vorgegebenen Tiefpassfunktion  $H_{\rm TP}(f)$  erhält man weiter:

$$H_{\rm HP}(f) = 1 - \frac{1}{1 + {\rm j} \cdot f / f_{\rm G}} = \frac{{\rm j} \cdot f / f_{\rm G}}{1 + {\rm j} \cdot f / f_{\rm G}} .$$

• Für  $f = 0$  ergibt sich  $H_{\rm HP}(f = 0) \;\underline{= 0}$. Anzumerken ist, dass die tatsächliche (komplexe) Funktion  $H_{\rm TP}(f)$  und nicht deren Betrag zu substrahieren ist. Daher ist die obige Skizze nur qualitativ zu verstehen.

Zum genau gleichen Ergebnis kommt man ausgehend von der konkreten Schaltung auf der Angabenseite. Entsprechend einem frequenzabhängigen Spannungsteiler mit den Widerständen  $R$  und  $1/(j\omega C)$  gilt:

$$H_{\rm HP}(f) = \frac{R}{R + 1/({\rm j}\cdot \omega \cdot C)} = \frac{{\rm j}\cdot \omega \cdot C \cdot R}{1+{\rm j} \cdot \omega \cdot C \cdot R} = \frac{{\rm j} \cdot f / f_{\rm G}}{1 + {\rm j} \cdot f / f_{\rm G}}.$$

(3)  Richtig sind die Lösungsvorschläge 2 und 3:

• Die Betragsfunktion des Hochpasses lautet:

$$|H_{\rm HP}(f)| = \frac{|f / f_{\rm G}|}{\sqrt{1 + ( f / f_{\rm G})^2}} .$$

• Bei der Grenzfrequenz  $f_{\rm G}$  sind somit die Beträge von Hochpass– und Tiefpass–Frequenzgang gleich groß, und zwar jeweils  $0.707$.
• Dagegen ist die erste Aussage offensichtlich falsch:  Demnach müsste sich nämlich der Wert  $|H_{HP}(f = f_{\rm G})| = 1 – 0.707 \approx 0.293$  ergeben.

Tiefpass– und Hochpass–Phasengang

• Der unter  (2)  berechnete Frequenzgang kann auch wie folgt dargestellt werden:

$$H_{\rm HP}(f) = \frac{( f / f_{\rm G})^2 + {\rm j} \cdot f / f_{\rm G}}{{1 + ( f / f_{\rm G})^2}} .$$

Damit ergibt sich für die Phasenfunktion:

$$\varphi_{\rm HP}(f) =-\arctan\frac{f / f_{\rm G}}{( f / f_{\rm G})^2}= -{\rm arcctg} ({f}/{f_{\rm G}})$$

$$\Rightarrow \hspace{0.3cm}\varphi_{\rm HP}(f) = {\rm arctan} (\frac{f}{f_{\rm G}}) - \frac{\pi}{2}= \varphi_{\rm TP}(f)- \frac{\pi}{2}.$$

• Bei positiven Frequenzen ergibt sich also bis auf eine Verschiebung um  $\pi /2$  nach unten der gleiche Verlauf wie beim Tiefpass-System. Da die Phasenfunktion ungerade ist, gibt es bei negativen Frequenzen eine Verschiebung um  $\pi /2$  nach oben.

(4)  Richtig sind die Lösungsvorschläge 2 und 3:

• Aufgrund der Linearität der Fourier(rück)transformation gilt für den Zeitverlauf für  $t > 0$:

$$h_{\rm HP}(t) = h_1(t) - h_2(t)= \delta(t) - \frac{1}{\tau}\cdot {\rm e}^{-t / \tau} .$$

• Die Diracfunktion ist die Fourierrücktransformierte der konstanten Frequenzfunktion „1”.
• Der zweite Anteil ist bis auf das Vorzeichen identisch mit der TP–Impulsantwort.
• Die Diracfunktion bewirkt, dass  $h_{\rm HP}(t)$  zum Zeitpunkt  $t = 0$  unendlich groß ist. Dagegen gilt für  $t = \tau$:

$$h_{\rm HP}(t = \tau) = - \frac{1}{\tau}\cdot {\rm e}^{-1} = - {{\rm e}\cdot \tau}^{-1}.$$

• Die letzte Aussage ist somit aufgrund des Vorzeichens ebenfalls falsch.