Aufgaben:Exercise 4.2: Rectangular Spectra

• Return to book

Rechteckförmige Tiefpass– und Bandpass–Spektren

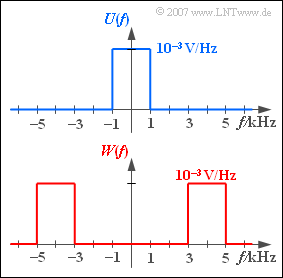
Wir betrachten zwei Signale  $u(t)$  und  $w(t)$  mit jeweils rechteckförmigen Spektren  $U(f)$  bzw.  $W(f)$.

• Es ist offensichtlich, dass

$$u(t) = u_0 \cdot {\rm si} ( \pi \cdot {t}/{T_{ u}})$$

ein Tiefpass–Signal ist, dessen zwei Parameter  $u_0$  und  $T_u$  in der Teilaufgabe  (1)  zu bestimmen sind.

• Dagegen zeigt das Spektrum  $W(f)$, dass  $w(t)$  ein Bandpass–Signal beschreibt.

In dieser Aufgabe wird außerdem auf das Bandpass–Signal

$$d(t) = 10 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 5 \pi f_2 \hspace{0.05cm}t) - 6 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 3 \pi f_2\hspace{0.05cm} t)$$

Bezug genommen, dessen Spektrum in  Aufgabe 4.1  ermittelt wurde. Es sei  $f_2 = 2 \ \rm kHz.$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Unterschiede und Gemeinsamkeiten von Tiefpass– und Bandpass–Signalen.

• Berücksichtigen Sie bei der Lösung die folgende trigonometrische Beziehung:

$$\sin (\alpha) \cdot \cos (\beta) = {1}/{2} \cdot \big[ \sin (\alpha + \beta)+ \sin (\alpha - \beta)\big].$$

Fragebogen

1

Welche Werte besitzen die Parameter  $u_0$  und  $T_u$  des Tiefpass–Signals?

$u_0\ = \ $  $\text{V}$

$T_u\ = \ $  $\text{ms}$

2

Berechnen Sie das Bandpass–Signal  $w(t)$. Wie groß sind die Signalwerte bei  $t = 0$  und  $t = 62.5 \, {\rm µ}\text{s}$?

$w(t=0)\ = \ $  $\text{V}$

$w(t=62.5 \,{\rm µ} \text{s})\ = \ $  $\text{V}$

3

Welche Aussagen sind bezüglich der Bandpass–Signale  $d(t)$  und  $w(t)$  zutreffend? Begründen Sie Ihr Ergebnis im Zeitbereich.

	Die Signale  $d(t)$  und  $w(t)$  sind identisch.
	$d(t)$  und  $w(t)$  unterscheiden sich durch einen konstanten Faktor.
	$d(t)$  und  $w(t)$  haben unterschiedliche Form.

Musterlösung

Solution

(1)  Die Zeit  $T_u$   ⇒   erste Nullstelle des TP–Signals  $u(t)$  – ist gleich dem Kehrwert der Breite des Rechteckspektrums, also  $1/(2\, \text{kHz} ) \hspace{0.15 cm}\underline{= 0.5 \, \text{ms}}$.

• Die Impulsamplitude ist wie in der Musterlösung zur  Aufgabe 4.1  dargelegt wurde, gleich der Rechteckfläche. Daraus folgt  $u_0\hspace{0.15 cm}\underline{= 2 \, \text{V}}$.

Multiplikation mit Cosinus

(2)  Das Bandpass–Spektrum kann mit  $f_{\rm T} = 4\, \text{kHz}$  wie folgt dargestellt werden:

$$W(f) = U(f- f_{\rm T}) + U(f+ f_{\rm T}) = U(f)\star \left[ \delta(f- f_{\rm T})+ \delta(f+ f_{\rm T})\right].$$

Entsprechend dem  Verschiebungssatz  gilt dann für das dazugehörige Zeitsignal:

$$w(t) = 2 \cdot u(t) \cdot {\cos} ( 2 \pi f_{\rm T} t) = 2 u_0 \cdot {\rm si} ( \pi {t}/{T_{\rm u}})\cdot {\cos} ( 2 \pi f_{\rm T} t).$$

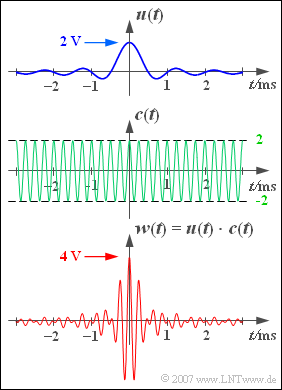
Die Grafik zeigt

• oben das Tiefpass–Signal $u(t)$,
• dann die Schwingung $c(t) = 2 · \cos(2 \pi fTt$ ),
• unten das Bandpass–Signal  $w(t) = u(t) \cdot c(t)$.

Insbesondere erhält man zum Zeitpunkt  $t = 0$:

$$w(t = 0) = 2 \cdot u_0 \hspace{0.15 cm}\underline{= 4 \hspace{0.05cm}{\rm V}}.$$

Der Zeitpunkt  $t=62.5 \,{\rm µ} \text{s}$  entspricht genau einer viertel Periodendauer des Signals  $c(t)$:

$$w(t = 62.5 \hspace{0.05cm}{\rm µ s}) = 2 u_0 \cdot {\rm si} ( \pi \cdot \frac{62.5 \hspace{0.05cm}{\rm µ s}} {500 \hspace{0.05cm}{\rm µ s}}) \cdot {\cos} ( 2 \pi \cdot 4\hspace{0.05cm}{\rm kHz}\cdot 62.5 \hspace{0.05cm}{\rm µ s})$$

$$\Rightarrow \hspace{0.3cm}w(t = 4\hspace{0.05cm}{\rm V}\cdot{\rm si} ( {\pi}/{8}) \cdot \cos ( {\pi}/{4})\hspace{0.15 cm}\underline{ = 0}.$$

(3)  Richtig ist der Lösungsvorschlag 1:

• Vergleicht man die Spektralfunktion  $W(f)$  dieser Aufgabe mit dem Spektrum  $D(f)$  in der Musterlösung zu  Aufgabe 4.1, so erkennt man, dass  $w(t)$  und  $d(t)$  identische Signale sind.
• Etwas aufwändiger ist dieser Beweis im Zeitbereich. Mit  $f_2 = 2 \,\text{kHz}$  kann für das hier betrachtete Signal geschrieben werden:

$$w(t ) = 4\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi f_2 t) \cdot {\cos} ( 4 \pi f_2 t) = ({4\hspace{0.05cm}{\rm V}})/({\pi f_2 t})\cdot \sin (\pi f_2 t) \cdot \cos ( 4 \pi f_2 t) .$$

• Wegen der trigonometrischen Beziehung

$$\sin (\alpha) \cdot \cos (\beta) = {1}/{2} \cdot \big[ \sin (\alpha + \beta)+ \sin (\alpha - \beta)\big]$$

kann obige Gleichung umgeformt werden:

$$w(t ) = \frac{2\hspace{0.05cm}{\rm V}}{\pi f_2 t}\cdot \big [\sin (5\pi f_2 t) + \sin (-3\pi f_2 t)\big ] = 10\hspace{0.05cm}{\rm V} \cdot \frac{\sin (5\pi f_2 t)}{5\pi f_2 t}- 6\hspace{0.05cm}{\rm V} \cdot \frac{\sin (3\pi f_2 t)}{3\pi f_2 t}.$$

• Damit ist gezeigt, dass beide Signale tatsächlich identisch sind   ⇒   Lösungsvorschlag 1:

$$w(t) = 10 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 5 \pi f_2 t) - 6 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 3 \pi f_2 t) = d(t).$$