Difference between revisions of "Aufgaben:Exercise 2.1Z: 2D-Frequency and 2D-Time Representations"
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Allgemeine Beschreibung zeitvarianter Systeme}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Allgemeine Beschreibung zeitvarianter Systeme}} | ||
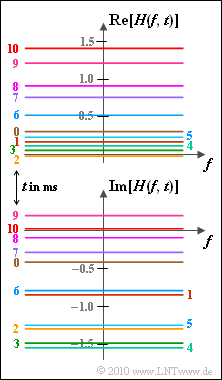
| − | [[File:P_ID2145__Mob_z_2_1.png|right|frame|2D transfer function: real and imaginary parts]] | + | [[File:P_ID2145__Mob_z_2_1.png|right|frame|2D transfer function: <br>real and imaginary parts]] |
| − | To describe a time-variant channel with several paths, the | + | To describe a time-variant channel with several paths, the '''two-dimensional impulse response''' is used: |
| − | $$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$ | + | :$$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$ |
| − | The first parameter $(\tau)$ indicates the delay, the second $(t)$ is related to the time variance of the channel. | + | The first parameter $(\tau)$ indicates the delay, the second parameter $(t)$ is related to the time variance of the channel. |
| − | The Fourier transform of $h(\tau, t)$ | + | The Fourier transform of $h(\tau, \ t)$ with respect to $\tau$ is the '''time-variant transfer function''': |
:$$H(f,\hspace{0.05cm} t) | :$$H(f,\hspace{0.05cm} t) | ||
\hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In the graph, $H(f, t)$ is displayed as a function of frequency, for different values of absolute time $t$ in the range of $0 \ \text{...} \ 10 \ \rm ms$. | + | *In the graph, $H(f, \ t)$ is displayed as a function of frequency, for different values of absolute time $t$ in the range of $0 \ \text{...} \ 10 \ \rm ms$. |
| − | In general, $H(f, t)$ is complex. The real part (top) and the imaginary part (bottom) are drawn separately. | + | *In general, $H(f, \ t)$ is complex. The real part (top) and the imaginary part (bottom) are drawn separately. |
| Line 25: | Line 25: | ||
''Notes:'' | ''Notes:'' | ||
* This task belongs to the chapter [[Mobile_Communications/General_Description_of_Time_Variant_Systems|General description of time–variant systems]]. | * This task belongs to the chapter [[Mobile_Communications/General_Description_of_Time_Variant_Systems|General description of time–variant systems]]. | ||
| − | * In the above equation, an single-path channel is represented with | + | * In the above equation, an single-path channel is represented with parameter $M = 1$ . |
* Here are some numerical values of the specified time-variant transfer function: | * Here are some numerical values of the specified time-variant transfer function: | ||
| − | $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\, {\rm ms}) \approx 0.3 - {\rm j} \cdot 0.4 \hspace{0.05cm},\hspace{0.2cm} | + | :$$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\, {\rm ms}) \approx 0.3 - {\rm j} \cdot 0.4 \hspace{0.05cm},\hspace{0.2cm} |
H(f,\hspace{0.05cm} t = 2\, {\rm ms}) \approx 0.0 - {\rm j} \cdot 1.3 \hspace{0.05cm},$$ | H(f,\hspace{0.05cm} t = 2\, {\rm ms}) \approx 0.0 - {\rm j} \cdot 1.3 \hspace{0.05cm},$$ | ||
| − | $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\, {\rm ms}) \approx 0.1 - {\rm j} \cdot 1.5 \hspace{0.05cm},\hspace{0.2cm} | + | :$$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\, {\rm ms}) \approx 0.1 - {\rm j} \cdot 1.5 \hspace{0.05cm},\hspace{0.2cm} |
H(f,\hspace{0.05cm} t = 6\, {\rm ms}) \approx 0.5 - {\rm j} \cdot 0.8 \hspace{0.05cm},$$ | H(f,\hspace{0.05cm} t = 6\, {\rm ms}) \approx 0.5 - {\rm j} \cdot 0.8 \hspace{0.05cm},$$ | ||
| − | $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 8\, {\rm ms}) \approx 0.9 - {\rm j} \cdot 0.1 \hspace{0.05cm},\hspace{0.2cm} | + | :$$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 8\, {\rm ms}) \approx 0.9 - {\rm j} \cdot 0.1 \hspace{0.05cm},\hspace{0.2cm} |
H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$ | H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$ | ||
| − | * As can already be guessed from the above graph, neither the real nor the imaginary part of the 2D transfer function $H(f, t)$ are zero-mean. | + | * As can already be guessed from the above graph, neither the real nor the imaginary part of the 2D transfer function $H(f, \ t)$ are zero-mean. |
| Line 52: | Line 52: | ||
{How can the 2D impulse response be described here? | {How can the 2D impulse response be described here? | ||
|type="[]"} | |type="[]"} | ||
| − | - $h(\tau, t) = A \cdot \delta(\tau) + B \cdot \delta(\tau \, –5 \, \rm µ s)$. | + | - $h(\tau, \ t) = A \cdot \delta(\tau) + B \cdot \delta(\tau \, –5 \, \rm µ s)$. |
| − | - $h(\tau, t) = A \cdot \delta(\tau)$. | + | - $h(\tau, \ t) = A \cdot \delta(\tau)$. |
| − | + $h(\tau, t) = z(t) \cdot \delta(\tau)$. | + | + $h(\tau, \ t) = z(t) \cdot \delta(\tau)$. |
| − | {Estimate | + | {Estimate for which channel the data was recorded. |
|type="()"} | |type="()"} | ||
- AWGN channel, | - AWGN channel, | ||
Revision as of 17:48, 14 December 2020
To describe a time-variant channel with several paths, the two-dimensional impulse response is used:
- $$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$
The first parameter $(\tau)$ indicates the delay, the second parameter $(t)$ is related to the time variance of the channel.
The Fourier transform of $h(\tau, \ t)$ with respect to $\tau$ is the time-variant transfer function:
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.$$
- In the graph, $H(f, \ t)$ is displayed as a function of frequency, for different values of absolute time $t$ in the range of $0 \ \text{...} \ 10 \ \rm ms$.
- In general, $H(f, \ t)$ is complex. The real part (top) and the imaginary part (bottom) are drawn separately.
Notes:
- This task belongs to the chapter General description of time–variant systems.
- In the above equation, an single-path channel is represented with parameter $M = 1$ .
- Here are some numerical values of the specified time-variant transfer function:
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\, {\rm ms}) \approx 0.3 - {\rm j} \cdot 0.4 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 2\, {\rm ms}) \approx 0.0 - {\rm j} \cdot 1.3 \hspace{0.05cm},$$
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\, {\rm ms}) \approx 0.1 - {\rm j} \cdot 1.5 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 6\, {\rm ms}) \approx 0.5 - {\rm j} \cdot 0.8 \hspace{0.05cm},$$
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 8\, {\rm ms}) \approx 0.9 - {\rm j} \cdot 0.1 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$
- As can already be guessed from the above graph, neither the real nor the imaginary part of the 2D transfer function $H(f, \ t)$ are zero-mean.
Questionnaire
Sample solution
(2) If we look at a fixed point in time, for example $t = 2 \ \rm ms$, we obtain the following for the time-variant transfer function
$$H(f,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \hspace{0.05cm} = {\rm const.}$$
Thus the corresponding 2D–impulse response is $$h(\tau,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \cdot \delta (\tau) \hspace{0.05cm} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} M = 1 \hspace{0.05cm}.$$
There is only one path ($M=1$). This means that the correct solution is NO.
(3) The correct solution is solution 3:
- There is time variance but no frequency selectivity.
- Options 1 and 2, on the other hand, describe time-invariant systems.
(4) Solution 4 is correct:
- For the AWGN channel, no transfer function can be specified.
- For a two-way channel, $H(f, t)$ is not constant in $f$ for any $t$.
- Since in the $H(f, t)$ graph the real and imaginary part have a non-zero mean, the Rayleigh–channel can also be excluded.
- The data for the present task comes from a Rice channel with the following parameters:
- $$\sigma = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} x_0 = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm}y_0 = -{1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} f_{\rm D,\hspace{0.05cm} max} = 100\,\,{\rm Hz}\hspace{0.05cm}.$$