Aufgaben:Exercise 1.2Z: Puls Code Modulation

• Return to book

Components of pulse code modulation

All modern communication systems are digital. The principle of digital transmission of speech signals goes back to  Alec Reeves , who invented the so-called  Pulscodemodulation  (PCM)  as early as 1938.

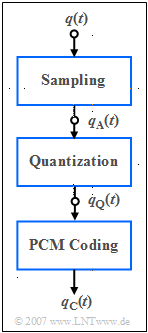
On the right you see the (simplified) block diagram of the PCM transmitter with three functional units:

• The band-limited speech signal  ${q(t)}$  is sampled, where the  Abtasttheorem  is observed, and yields the sampled signal  $q_{\rm A}(t)$.
• Each sample  $q_{\rm A}(t)$  is mapped to one of  $M = 2^N$  results in the quantized signal  $q_{\rm Q}(t)$.
• Each individual quantized value is represented by a code sequence of  $N$  binary symbols and results in the coded signal  $q_{\rm C}(t)$.

In this task only the different signals of the PCM transmitter are to be classified. Later tasks will deal with other properties of pulse code modulation.

Notes:   This task belongs to the chapter  Signal classification.

Questions

1

Which of the statements are true for the source signal  ${q(t)}$ ?

	In normal operation  ${q(t)}$  is a stochastic signal.
	A deterministic source signal is only useful in test operation or for theoretical investigations.
	${q(t)}$  is a time-discrete signal.
	${q(t)}$  is a continuous-valued signal.

2

Which of the statements apply to the sampled signal  $q_{\rm A}(t)$ ?

	$q_{\rm A}(t)$  is a discrete-valued signal.
	$q_{\rm A}(t)$  is a time-discrete signal.
	The higher the maximum frequency of the message signal, the higher the sampling rate must be selected.

3

Which statements are true for the quantized signal  $q_{\rm Q}(t)$  if  $N = 8$  is taken as a base?

	$q_{\rm Q}(t)$  is a time-discrete signal.
	$q_{\rm Q}(t)$  is a discrete-valued with signal  $M = 8$  possible values.
	$q_{\rm Q}(t)$  is a discrete-valued with signal  $M = 256$  possible values.
	$q_{\rm Q}(t)$  is a binary signal.

4

Which statements are true for the coded signal  $q_{\rm C}(t)$  if  $N = 8$  is taken as a basis?

	$q_{\rm C}(t)$  is a time-discrete signal.
	$q_{\rm C}(t)$  is a discrete-valued signal with  $M = 8$  possible values.
	$q_{\rm C}(t)$  is a binary signal.
	When sampling at distance  $T_{\rm A}$  the bit duration is  $T_{\rm B} = T_{\rm A}$.
	When sampling at distance  $T_{\rm A}$  the bit duration is  $T_{\rm B} = T_{\rm A}/8$.

Solution

Solution

(1)  Correct are the solutions 1, 2 and 4:

• The source signal  ${q(t)}$  is analog, i.e. continuous in time and value.
• In general, it makes no sense to transmit a deterministic signal.
• For the mathematical description, a deterministic source signal – such as a periodic signal – is better suited than a random signal.
• Deterministic signals are also used for testing in order to be able to reconstruct detected errors.

(2)  Correct are the solution suggestions 2 and 3:

• The signal  $q_{\rm A}(t)$  after sampling is still  value-continuous, but now  time-discrete.
• The sampling frequency  $f_{\rm A}$  is given by the so-called  sampling theorem .
• The greater the maximum frequency  $f_{\rm N,\,max}$  of the message signal, the greater must  $f_{\rm A} ≥ 2 \cdot f_{\rm N,\,max}$  can be selected.

(3)  Correct are the solution suggestions 1 and 3:

• The quantized signal  $q_{\rm Q}(t)$  is time and value discrete, where the number of steps are  $M = 2^8 = 256$ 
• A binary signal, on the other hand, is a discrete value signal with the number of steps  $M = 2$.

(4)  Correct here are the solutions 1, 3 and 5:

• The coded signal  $q_{\rm C}(t)$  is binary  $($level number  $M = 2)$  with bit duration  $T_{\rm B} = T_{\rm A}/8$.