Difference between revisions of "Aufgaben:Exercise 2.2: Simple Two-Path Channel Model"
| Line 74: | Line 74: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' We have $\tau_1 = d_1/c$ ⇒ $ d_1 = \tau_1 \cdot c = 10^{-5} \rm s \cdot 3 \cdot 10^8 \ m/s \ \ \underline {= 3 \ km}$. | + | '''(1)''' We have $\tau_1 = d_1/c$ ⇒ $ d_1 = \tau_1 \cdot c = 10^{-5} \rm s \cdot 3 \cdot 10^8 \ m/s \ \ \underline {= 3 \ km}$. |
| − | '''(2)''' The damping factor is $k_0 = k_2/k_1 \ \ \underline {= 0.2}$ and the delay time $\tau_0 = \tau_2 \ | + | '''(2)''' The damping factor is $k_0 = k_2/k_1 \ \ \underline {= 0.2}$ and the delay time $\tau_0 = \tau_2 \ - \tau_1 \ \underline {= 1 \ \ \rm µ s}$. |
| − | *The path loss | + | *The effective path loss for both paths is thus $k_1 = 10^{-4}$ and the basic delay time is $\tau_1 = 10 \ \ \rm µ s$. |
| + | |||
'''(3)''' The impulse location is | '''(3)''' The impulse location is | ||
| − | $$h_{\rm 0}(\tau) = \delta(\tau) + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$ | + | :$$h_{\rm 0}(\tau) = \delta(\tau) + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$ |
By Fourier transformation you get the frequency response | By Fourier transformation you get the frequency response | ||
| Line 89: | Line 90: | ||
and thus to the following magnitude of the frequency response: | and thus to the following magnitude of the frequency response: | ||
| − | $$|H_{\rm 0}(f)| = \sqrt{ \left [ 1 + k_0 \cdot {\cos}( 2 \pi f \tau_0)\right ]^2 + k_0^2 \cdot {\sin^2 }( 2 \pi f \tau_0)}\hspace{0.3cm} | + | :$$|H_{\rm 0}(f)| = \sqrt{ \left [ 1 + k_0 \cdot {\cos}( 2 \pi f \tau_0)\right ]^2 + k_0^2 \cdot {\sin^2 }( 2 \pi f \tau_0)}\hspace{0.3cm} |
\Rightarrow \hspace{0.3cm}|H_{\rm 0}(f = 0)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1+ k_0 \hspace{0.1cm} \underline {=1.2} \hspace{0.05cm},$$ | \Rightarrow \hspace{0.3cm}|H_{\rm 0}(f = 0)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1+ k_0 \hspace{0.1cm} \underline {=1.2} \hspace{0.05cm},$$ | ||
| − | $$|H_{\rm 0}(f = 250\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi/2)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi/2)} = \sqrt{1+ k_0^2} \hspace{0.1cm} \underline {\approx 1.02} \hspace{0.05cm},$$ | + | :$$|H_{\rm 0}(f = 250\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi/2)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi/2)} = \sqrt{1+ k_0^2} \hspace{0.1cm} \underline {\approx 1.02} \hspace{0.05cm},$$ |
| − | $$|H_{\rm 0}(f = 500\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi)} = {1- k_0} \hspace{0.1cm} \underline {= 0.8} \hspace{0.05cm}.$$ | + | :$$|H_{\rm 0}(f = 500\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi)} = {1- k_0} \hspace{0.1cm} \underline {= 0.8} \hspace{0.05cm}.$$ |
[[File:P_ID2158__Mob_A_2_2c.png|right|frame|Magnitude of the frequency response of a two-way channel]] | [[File:P_ID2158__Mob_A_2_2c.png|right|frame|Magnitude of the frequency response of a two-way channel]] | ||
| − | The graphic (red curve) shows the function $|H_0(f)|$. | + | The graphic (red curve) shows the function $|H_0(f)|$. |
*The values you are looking for are marked by the yellow dots. | *The values you are looking for are marked by the yellow dots. | ||
| − | *The blue curve refers to | + | *The blue curve refers to '''(5)''' with $k_0 = 1 \ \Rightarrow \ k_2 = k_0 \cdot k_1 = 10^{-4}$. |
'''(4)''' <u>Solution 1</u> is correct: | '''(4)''' <u>Solution 1</u> is correct: | ||
| − | *Destructive interference occurs for $|H_0(f)| < 1$, | + | *Destructive interference occurs for $|H_0(f)| < 1$, e.g. for $f = 500 \ \rm kHz$. |
*On the other hand: | *On the other hand: | ||
:$$|H_{\rm 0}(f = 750\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 250\,{\rm kHz})| \approx 1.02 > 1\hspace{0.05cm},$$ | :$$|H_{\rm 0}(f = 750\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 250\,{\rm kHz})| \approx 1.02 > 1\hspace{0.05cm},$$ | ||
| Line 108: | Line 109: | ||
| − | '''(5)''' The difference $\tau_{\rm max} | + | '''(5)''' The difference $\tau_{\rm max} - \tau_{\rm min}$ between the delays in the two paths is equal to $\tau_0 = 1 \ \ \rm µ s$. |
*So the coherence bandwidth is | *So the coherence bandwidth is | ||
:$$B_{\rm K}\hspace{0.01cm}' = {1}/{\tau_{\rm 0} } \hspace{0.1cm} \underline {=1\,{\rm MHz}} \hspace{0.05cm}.$$ | :$$B_{\rm K}\hspace{0.01cm}' = {1}/{\tau_{\rm 0} } \hspace{0.1cm} \underline {=1\,{\rm MHz}} \hspace{0.05cm}.$$ | ||
| − | *The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow k_0 = $ | + | *The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow \ k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow \ k_0 = 1$ in the same way. |
| − | *This approximation $B_{\rm K}\hspace{0.01cm}'$ of the coherence bandwidth is shown in the graph. | + | *This approximation $B_{\rm K}\hspace{0.01cm}'$ of the coherence bandwidth is shown in the graph. |
'''(6)''' <u>Solution 2</u> is correct: | '''(6)''' <u>Solution 2</u> is correct: | ||
| − | *The channel is non | + | *The channel is non–frequency–selective if the coherence bandwidth $B_{\rm K}$ is significantly larger than the signal bandwidth $B_{\rm S}$. |
| − | *For the given channel, this is true for GSM, but not for UMTS. For UMTS, this is frequency | + | *For the given channel, this is true for GSM, but not for UMTS. For UMTS, this is a frequency selective channel. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Exercises for Mobile Communications|^2.2 Multi-Path Reception in Wireless Systems^]] | [[Category:Exercises for Mobile Communications|^2.2 Multi-Path Reception in Wireless Systems^]] | ||
Revision as of 15:55, 11 January 2021
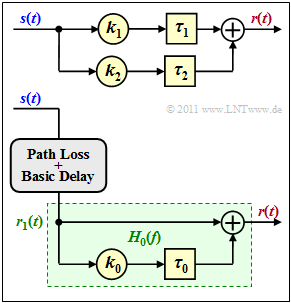
Here we consider a two-path channel for mobile radio according to the adjacent graph, characterized by the model parameters
- $$k_1 = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} \tau_{1} = 10\,{\rm µ s}\hspace{0.05cm}, \hspace{0.2cm}\tau_{2} = 11\,{\rm µ s} \hspace{0.05cm}.$$
Two different numerical values are considered for the damping factor on the secondary path:
- $k_2 = 2 \cdot 10^{-5}$ ⇒ subtasks (1) to (4),
- $k_2 = 10^{-4}$ ⇒ subtasks (5) and (6).
An equivalent channel model is shown below, with only the part highlighted in green being considered further. This means:
- The basic attenuation (path loss) and the basic propagation time are not taken into account here.
- The frequency response of this $(k_0, \tau_0$)–model is designated $H_0(f)$.
An important descriptive parameter of any mobile radio system is the coherence bandwidth $B_{\rm K}$, which is defined in the chapter The GWSSUS Channel Model . The coherence bandwidth indicates whether the system can be approximated as non–frequency–selective:
- This is justified if the signal bandwidth $B_{\rm S}$ is significantly smaller than the coherence bandwidth $B_{\rm K}$.
- Otherwise, the mobile radio system is frequency–selective, which requires a more complicated description.
As a simple approximation for the coherence bandwidth, the reciprocal value of pulse broadening is often used in the literature (marked by an apostrophe in our tutorial):
- $$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$
Notes:
- This task belongs to the topic of the chapter Multi–Path Reception in Mobile Communications.
- For the solution you also need the speed of light $c = 3 \cdot 10^8 \ \rm m/s$.
- For $k_2$ only positive values are used here. However, as you may remember, if the secondary path is created by reflection on a wall, a phase change by $\pi$ occurs, resulting in a negative value of $k_2$.
Questionnaire
Solution
(2) The damping factor is $k_0 = k_2/k_1 \ \ \underline {= 0.2}$ and the delay time $\tau_0 = \tau_2 \ - \tau_1 \ \underline {= 1 \ \ \rm µ s}$.
- The effective path loss for both paths is thus $k_1 = 10^{-4}$ and the basic delay time is $\tau_1 = 10 \ \ \rm µ s$.
(3) The impulse location is
- $$h_{\rm 0}(\tau) = \delta(\tau) + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$
By Fourier transformation you get the frequency response
- $$H_{\rm 0}(f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + k_0 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_0}=1 + k_0 \cdot {\cos}( 2 \pi f \tau_0) + {\rm j}\cdot k_0 \cdot {\sin }( 2 \pi f \tau_0) \hspace{0.05cm},$$
and thus to the following magnitude of the frequency response:
- $$|H_{\rm 0}(f)| = \sqrt{ \left [ 1 + k_0 \cdot {\cos}( 2 \pi f \tau_0)\right ]^2 + k_0^2 \cdot {\sin^2 }( 2 \pi f \tau_0)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}|H_{\rm 0}(f = 0)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1+ k_0 \hspace{0.1cm} \underline {=1.2} \hspace{0.05cm},$$
- $$|H_{\rm 0}(f = 250\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi/2)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi/2)} = \sqrt{1+ k_0^2} \hspace{0.1cm} \underline {\approx 1.02} \hspace{0.05cm},$$
- $$|H_{\rm 0}(f = 500\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi)} = {1- k_0} \hspace{0.1cm} \underline {= 0.8} \hspace{0.05cm}.$$
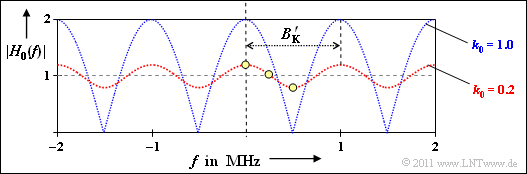
The graphic (red curve) shows the function $|H_0(f)|$.
- The values you are looking for are marked by the yellow dots.
- The blue curve refers to (5) with $k_0 = 1 \ \Rightarrow \ k_2 = k_0 \cdot k_1 = 10^{-4}$.
(4) Solution 1 is correct:
- Destructive interference occurs for $|H_0(f)| < 1$, e.g. for $f = 500 \ \rm kHz$.
- On the other hand:
- $$|H_{\rm 0}(f = 750\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 250\,{\rm kHz})| \approx 1.02 > 1\hspace{0.05cm},$$
- $$|H_{\rm 0}(f = 1\,{\rm MHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 0)| = 1.2 > 1 \hspace{0.05cm}.$$
(5) The difference $\tau_{\rm max} - \tau_{\rm min}$ between the delays in the two paths is equal to $\tau_0 = 1 \ \ \rm µ s$.
- So the coherence bandwidth is
- $$B_{\rm K}\hspace{0.01cm}' = {1}/{\tau_{\rm 0} } \hspace{0.1cm} \underline {=1\,{\rm MHz}} \hspace{0.05cm}.$$
- The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow \ k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow \ k_0 = 1$ in the same way.
- This approximation $B_{\rm K}\hspace{0.01cm}'$ of the coherence bandwidth is shown in the graph.
(6) Solution 2 is correct:
- The channel is non–frequency–selective if the coherence bandwidth $B_{\rm K}$ is significantly larger than the signal bandwidth $B_{\rm S}$.
- For the given channel, this is true for GSM, but not for UMTS. For UMTS, this is a frequency selective channel.