Difference between revisions of "Aufgaben:Exercise 2.3Z: Oscillation Parameters"
From LNTwww
| Line 15: | Line 15: | ||
| − | + | A second form of representation is with the base frequency $f_0$ and the phase $\varphi$: | |
:$$x(t)=C \cdot\cos(2\pi f_0t-\varphi).$$ | :$$x(t)=C \cdot\cos(2\pi f_0t-\varphi).$$ | ||
| − | + | From a harmonic oscillation it is now known that | |
| + | :* the first signal maximum occurs at $t_1 = 2 \,\text{ms}$ auftritt, | ||
| − | :* | + | :* the second signal maximum occurs at $t_2 = 14 \,\text{ms}$ auftritt, |
| − | :* | + | :* the value $x_0 ={x(t = 0)} = 3 \,\text{V}$ . |
| − | |||
| Line 30: | Line 30: | ||
| − | + | ''Hint:'' | |
| − | '' | + | *This exercise belongs to the chapter [[ Signal_Representation/Harmonic_Oscillation|Harmonic Oscillation]]. |
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | + | What is the period duration $T_0$ and the base frequency $f_0$? | |
|type="{}"} | |type="{}"} | ||
$T_0\hspace{0.2cm} = \ $ { 12 3% } $\text{ms}$ | $T_0\hspace{0.2cm} = \ $ { 12 3% } $\text{ms}$ | ||
| Line 46: | Line 45: | ||
| − | { | + | {What is the value of the shift $\tau$ and the phase $\varphi$ $($in $\text{degrees})$ ? |
|type="{}"} | |type="{}"} | ||
$\tau\hspace{0.25cm} = \ $ { 2 3% } $\text{ms}$ | $\tau\hspace{0.25cm} = \ $ { 2 3% } $\text{ms}$ | ||
| Line 52: | Line 51: | ||
| − | { | + | {What is the amplitude of the harmonic oscillation?? |
|type="{}"} | |type="{}"} | ||
${C}\ = \ $ { 6 3% } $\text{V}$ | ${C}\ = \ $ { 6 3% } $\text{V}$ | ||
| − | { | + | {What is the spectrum $X(f)$? What is the weight of the spectral line at $+f_0$ ? |
|type="{}"} | |type="{}"} | ||
$\text{Re}\big[X(f = f_0)\big]\ = \ $ { 1.5 3% } $\text{V}$ | $\text{Re}\big[X(f = f_0)\big]\ = \ $ { 1.5 3% } $\text{V}$ | ||
Revision as of 21:59, 13 January 2021
Every harmonic oscillation can also be written in the form
- $$x(t)=C\cdot\cos\bigg(2\pi \cdot \frac{t-\tau}{T_0}\bigg).$$
The oscillation is thus completely determined by three parameters:
- the amplitude $C$,
- the period duration $T_0$,
- the shift $\tau$ with respect to a cosine signal.
A second form of representation is with the base frequency $f_0$ and the phase $\varphi$:
- $$x(t)=C \cdot\cos(2\pi f_0t-\varphi).$$
From a harmonic oscillation it is now known that
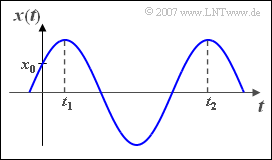
- the first signal maximum occurs at $t_1 = 2 \,\text{ms}$ auftritt,
- the second signal maximum occurs at $t_2 = 14 \,\text{ms}$ auftritt,
- the value $x_0 ={x(t = 0)} = 3 \,\text{V}$ .
Hint:
- This exercise belongs to the chapter Harmonic Oscillation.
Questions
Musterlösung
(1) Es gilt $T_0 = t_2 - t_1 = 12\, \text{ms}$ und $f_0 = 1/T_0 \hspace{0.15cm} \underline{\approx 83.33\, \text{Hz}}$.
(2) Die Verschiebung beträgt $\tau \hspace{0.1cm} \underline{= 2\, \text{ms}}$ und die Phase ist $\varphi = 2\pi \cdot \tau/T_0 = \pi/3$ entsprechend $\varphi =\hspace{0.15cm} \underline{60^{\circ}}$.
(3) Aus dem Wert zum Zeitpunkt $t = 0$ folgt für die Amplitude ${C}$:
- $$x_0=x(t=0)=C\cdot\cos(-60\,^\circ)={C}/{2}=\rm 3\,V \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm}\hspace{0.15cm}\underline{\it C=\rm 6\,V}.$$
(4) Die dazugehörige Spektralfunktion lautet:
- $$X(f)={C}/{2}\cdot{\rm e}^{-{\rm j}\varphi}\cdot\delta(f-f_0)+{C}/{2}\cdot{\rm e}^{{\rm j}\varphi}\cdot\delta(f+f_0).$$
- Das Gewicht der Diraclinie bei $f = f_0$ (erster Term) ist ${C}/2 \cdot {\rm e}^{–\text{j}\varphi} = 3 \,\text{V} \cdot \cos(60^\circ)- 3 \,\text{V} \cdot \sin(60^\circ)\hspace{0.05cm}\approx \underline{1.5 \,\text{V} - \text{j} \cdot 2.6 \,\text{V}}$.