Aufgaben:Exercise 2.5Z: Square Wave

• Return to book

Verschiedene Rechtecksignale

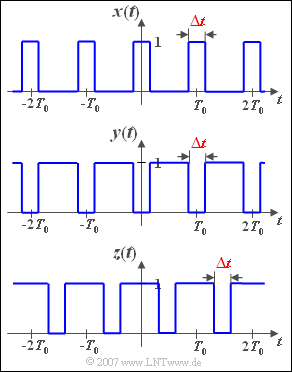
The signal  $x(t)$  periodic with time  $T_0$  is described by the single parameter  $\Delta t$ ; let the amplitude of the square-wave pulses be  $1$ in each case. Since  $x(t)$  is even, all sine coefficients  $B_n = 0$.

The DC signal coefficient is  $A_0 = \Delta t/T_0$  and the following applies to the cosine coefficients:

$$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$

In subtasks  (1)  and  (2)  the signal  $x(t)$  is analysed for the two parameter values  $\Delta t/T_0 = 0.5$  and  $\Delta t/T_0 = 0.25$  respectively.

Then we consider the two signals  $y(t)$  and  $z(t)$, each with  $\Delta t/T_0 = 0.25$. There is a fixed relationship between these signals and  $x(t)$  which can be exploited for the calculation.

Hints:

• This exercise belongs to the chapter  Fourier Series.
• You can find a compact summary of the topic in the two learning videos

Zur Berechnung der Fourierkoeffizienten,

Eigenschaften der Fourierreihendarstellung.

Questions

1

Whcih statements are true for the signal  $x(t)$  with  $\Delta t/T_0 = 0.5$?

	The spectral function  ${X(f)}$  contains a Dirac function at  $f = 0$  with the weight  $0.5$.
	The spectral function  ${X(f)}$  contains Dirac lines at all multiples of the base frequency  $f_0 = 1/T_0$.
	The spectral function  ${X(f)}$  contains diraclines at odd multiples of the base frequency   $f_0$.
	The spectral line at  $f_0$  has the weight  $2/\pi = 0.636$.
	The spectral line at  $–\hspace{-0.1cm}f_0$  has the weight  $1/\pi = 0.318$.

2

Which statements are true for the signal  $x(t)$  with  $\Delta t/T_0 = 0.25$?

	The spectral function  ${X(f)}$  contains diraclines at all odd multiples of the base frequency  $f_0$.
	${X(f)}$  has diraclines at  $\pm2f_0$,  $\pm6f_0$,  $\pm10f_0$, etc.
	${X(f)}$  has diraclines at  $\pm4f_0$,  $\pm8f_0$,  $\pm12f_0$, etc.
	The spectral line at  $2f_0$  has the weight  $1/(2\pi) = 0.159$.

3

What is the DC component of the signal  ${y(t)}$?

$y(t)$:   $A_0 \ = \ $

4

Welcher Zusammenhang besteht zwischen den Signalen  $x(t)$  und  ${y(t)}$? Geben Sie mit Hilfe dieser Überlegungen die Fourierkoeffizienten von  ${y(t)}$ an.
Wie groß sind die Koeffizienten  $A_1$  und  $A_2$  dieses Signals?

$y(t)$:   $A_1\ = \ $

$\hspace{1cm}A_2 \ = \ $

5

Welcher Zusammenhang besteht zwischen den Signalen  ${y(t)}$  und  ${z(t)}$? Wie groß sind die Koeffizienten  $A_1$  und  $A_2$  des Signals  ${z(t)}$?
Überprüfen Sie das Ergebnis anhand der angebenen Koeffizienten des Signals  $x(t)$.

$z(t)$:   $A_1 \ = \ $

$\hspace{1cm}A_2 \ = \ $

Musterlösung

Solution

(1)  Richtig sind die Aussagen 1, 3 und 5:

• Die Spektralfunktion beinhaltet eine Diracfunktion bei $f = 0$ mit dem Gewicht $0.5$ (Gleichanteil) sowie weitere Spektrallinien bei ungeradzahligen Vielfachen ($n = \pm1, \pm3, \pm5,\text{...}$) von $f_0$.
• Die Gewichte bei $\pm f_0$ sind jeweils $A_1/2 = 1/\pi = 0.318$.

(2)  Richtig sind die Aussagen 1, 2 und 4:

• Bei allen ungeradzahligen Vielfachen der Grundfrequenz existieren Spektrallinien, zusätzlich noch bei den $2–{\rm fachen}$, $6–{\rm fachen}$ und $10–{\rm fachen}$.
• Beispielsweise gilt $A_1 = 1/\pi = 0.450$. Die Spektrallinie bei $2f_0$ hat somit das Gewicht $A_2/2 = 1/(2\pi) = 0.159$.
• Für $n = 4$, $n = 8$, usw. sind dagegen die Koeffizienten $A_n = 0$, da für die Sinusfunktion gilt:   $\sin(\pi) = \sin(2\pi) =\text{ ...} = 0$.

(3)  Aus der grafischen Darstellung des Signals ${y(t)}$ wird deutlich, dass $A_0 = 0.75$ gelten muss. Zum gleichen Ergebnis kommt man über die Beziehung:

$$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$

(4)  Es gilt ${y(t)} = 1 - x(t)$. Für $n \neq 0$ ergeben sich somit die gleichen Fourierkoeffizienten wie für das Signal $x(t)$, jedoch mit negativen Vorzeichen. Inbesondere gilt:

$$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$

$$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$

(5)  Es gilt ${z(t)} = y(t - T_0/2)$. Mit der Fourierreihendarstellung von ${y(t)}$ folgt daraus:

$$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$

$$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\text{...}$$

Damit erhält man:

$$A_1^{(z)}=-A_1^{(y)}={\sqrt2}/{\pi}\hspace{0.15cm}\underline{=+0.450}, \hspace {0.5cm} A_2^{(z)}=A_2^{(y)}=-{1}/{\pi}\hspace{0.15cm}\underline{=-0.318}.$$

Das gleiche Ergebnis erhält man ausgehend von den gegebenen Koeffizienten mit $\Delta t/T_0 = 0.75$:

$$A_1^{(z)}={2}/{\pi} \cdot \sin({3}/{4}\cdot \pi)={\sqrt2}/{\pi}, \hspace {0.5cm}A_2^{(z)}= {1}/{\pi} \cdot \sin({3}/{2} \cdot \pi) =-{1}/{\pi}.$$