Difference between revisions of "Aufgaben:Exercise 3.3Z: Rectangular Pulse and Dirac Delta"
From LNTwww
| Line 34: | Line 34: | ||
|type="[]"} | |type="[]"} | ||
+ The spectral value $X_1(f = 0)$ is equal to $10^{–3} \,\text{V/Hz}$. | + The spectral value $X_1(f = 0)$ is equal to $10^{–3} \,\text{V/Hz}$. | ||
| − | + $X_1(f)$ has zeros at | + | + $X_1(f)$ has zeros at the interval of $2 \,\text{kHz}$. |
| − | - $X_1(f)$ has zeros at | + | - $X_1(f)$ has zeros at the interval of $4 \,\text{kHz}$. |
| Line 41: | Line 41: | ||
|type="[]"} | |type="[]"} | ||
+ The spectral value $X_2(f = 0)$ ist gleich $10^{–3} \,\text{V/Hz}$. | + The spectral value $X_2(f = 0)$ ist gleich $10^{–3} \,\text{V/Hz}$. | ||
| − | - $X_2(f)$ has zeros at | + | - $X_2(f)$ has zeros at the interval of $2\, \text{kHz}$. |
| − | + $X_2(f)$ has zeros at | + | + $X_2(f)$ has zeros at the interval of $4 \,\text{kHz}$. |
| Line 61: | Line 61: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Proposed <u>solutions 1 and 2</u> are correct: |
| − | * | + | *The spectral value at frequency $f = 0$ is always equal to the area under the time function according to [[Signal_Representation/Fourier_Transform_and_Its_Inverse#The_First_Fourier_Integral|the first Fourier integral]] : |
:$$X( f ) = \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm{e}}^{ - {\rm{j2\pi }}ft} \hspace{0.1cm} {\rm d}t \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \;X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t )}\hspace{0.1cm} {\rm d}t.$$ | :$$X( f ) = \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm{e}}^{ - {\rm{j2\pi }}ft} \hspace{0.1cm} {\rm d}t \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \;X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t )}\hspace{0.1cm} {\rm d}t.$$ | ||
| − | * | + | *In the present case, the pulse area is always $A \cdot T = 10^{–3} \,\text{Vs} = 1\, \text{mV/Hz}$. |
| − | * | + | *Because of $T_1 = 500 \,µ\text{s}$ the spectrum $X_1(f)$ has zero crossings at the interval $f_1 = 1/T_1 = 2 \,\text{kHz}$ . |
| + | '''(2)''' Proposed <u>solutions 1 and 3</u> are correct: | ||
| + | *Due to equal pulse areas, the spectral value is not changed at the frequency $f = 0$ . | ||
| + | *The equidistant zero crossings now occur at the interval $f_2 = 1/T_2 = 4 \,\text{kHz}$ auf. | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(3)''' Zero crossings occur at multiples of $f_{10} = 1/T_{10} = 20 \,\text{kHz}$, and the spectral function is: | |
| − | '''(3)''' | ||
:$$X_{10} ( f ) = X_0 \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}f/f_{10} } ).$$ | :$$X_{10} ( f ) = X_0 \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}f/f_{10} } ).$$ | ||
| − | * | + | *At frequency $f = 2 \,\text{kHz}$ the argument of the $\rm si$-function is equal to $\pi/10$ $($or $18^{\circ})$: |
:$$X_{10} ( {f = 2\;{\rm{kHz}}}) = 10^{ - 3} \;{\rm{V/Hz}} \cdot \frac{{\sin ( {18^\circ } )}}{{{\rm{\pi /10}}}} \hspace{0.15 cm}\underline{= 0.984 \;{\rm{mV/Hz}}}{\rm{.}}$$ | :$$X_{10} ( {f = 2\;{\rm{kHz}}}) = 10^{ - 3} \;{\rm{V/Hz}} \cdot \frac{{\sin ( {18^\circ } )}}{{{\rm{\pi /10}}}} \hspace{0.15 cm}\underline{= 0.984 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
| | ||
| − | '''(4)''' | + | '''(4)''' In the limiting case $k \rightarrow \infty$ the then infinitely high and infinitely narrow [[Signal_Representation/Special_Cases_of_Impulse_Signals#Rectangular_Impulse|Rectangular impulse]] changes into the [[Signal_Representation/Special_Cases_of_Impulse_Signals#Dirac_Delta_Impulse|Dirac Delta impulse]] . |
| − | * | + | *Its spectrum is constant for all frequencies. |
| − | * | + | *Thus the spectral value $X_{\infty}(f = 2 \,\text{kHz})\hspace{0.15 cm}\underline{=1 \text{ mV/Hz}}$ also applies at the frequency $f = 2 \,\text{kHz}$ . |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 19:10, 23 January 2021
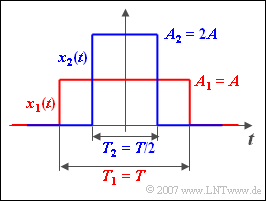
We consider here a multitude of symmetrical rectangular functions $x_k(t)$. The individual rectangles differ in amplitudes (heights)
- $$A_k = k \cdot A$$
and different pulse durations (widths)
- $$T_k = T/k.$$
Let $k$ be any positive value.
- The rectangular pulse $x_1(t)$ shown in red has the amplitude $A_1 = {A} = 2 \,\text{V}$ and the duration $T_1 = {T} = 500 \,µ\text{s}$.
- The pulse $x_2(t)$ shown in blue is half as wide ⇒ $T_2 =250 \,µ\text{s}$, but twice as high ⇒ $A_2 = 4 \text{ V}$.
Hints:
- This exercise belongs to the chapter Special Cases of Impulse Signals.
- You can check your results using the two interactive applets Impulse und Spektren sowie Frequenzgang und Impulsantwort .
Questions
Musterlösung
(1) Proposed solutions 1 and 2 are correct:
- The spectral value at frequency $f = 0$ is always equal to the area under the time function according to the first Fourier integral :
- $$X( f ) = \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm{e}}^{ - {\rm{j2\pi }}ft} \hspace{0.1cm} {\rm d}t \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \;X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t )}\hspace{0.1cm} {\rm d}t.$$
- In the present case, the pulse area is always $A \cdot T = 10^{–3} \,\text{Vs} = 1\, \text{mV/Hz}$.
- Because of $T_1 = 500 \,µ\text{s}$ the spectrum $X_1(f)$ has zero crossings at the interval $f_1 = 1/T_1 = 2 \,\text{kHz}$ .
(2) Proposed solutions 1 and 3 are correct:
- Due to equal pulse areas, the spectral value is not changed at the frequency $f = 0$ .
- The equidistant zero crossings now occur at the interval $f_2 = 1/T_2 = 4 \,\text{kHz}$ auf.
(3) Zero crossings occur at multiples of $f_{10} = 1/T_{10} = 20 \,\text{kHz}$, and the spectral function is:
- $$X_{10} ( f ) = X_0 \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}f/f_{10} } ).$$
- At frequency $f = 2 \,\text{kHz}$ the argument of the $\rm si$-function is equal to $\pi/10$ $($or $18^{\circ})$:
- $$X_{10} ( {f = 2\;{\rm{kHz}}}) = 10^{ - 3} \;{\rm{V/Hz}} \cdot \frac{{\sin ( {18^\circ } )}}{{{\rm{\pi /10}}}} \hspace{0.15 cm}\underline{= 0.984 \;{\rm{mV/Hz}}}{\rm{.}}$$
(4) In the limiting case $k \rightarrow \infty$ the then infinitely high and infinitely narrow Rectangular impulse changes into the Dirac Delta impulse .
- Its spectrum is constant for all frequencies.
- Thus the spectral value $X_{\infty}(f = 2 \,\text{kHz})\hspace{0.15 cm}\underline{=1 \text{ mV/Hz}}$ also applies at the frequency $f = 2 \,\text{kHz}$ .