Difference between revisions of "Aufgaben:Exercise 3.5Z: Integration of Dirac Functions"
From LNTwww
| Line 8: | Line 8: | ||
can be determined. Again, $A = 1 \,\text{V}$ and $T = 0.5 \,\text{ms}$ apply. | can be determined. Again, $A = 1 \,\text{V}$ and $T = 0.5 \,\text{ms}$ apply. | ||
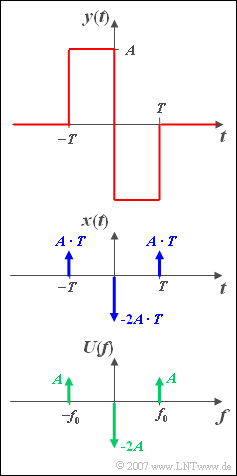
| − | + | Assume the time signal ${x(t)}$ according to the middle sketch, which is composed of three Dirac pulses at $–T$, $0$ and $+T$ with the pulse weights ${AT}$, $-2{AT}$ und ${AT}$ . | |
The spectral function ${X(f)}$ can be given directly by applying the [[Signal_Representation/Fourier_Transform_Laws#Vertauschungssatz|Vertauschungssatz]] if one takes into account that the time function belonging to ${U(f)}$ is as follows (see lower sketch): | The spectral function ${X(f)}$ can be given directly by applying the [[Signal_Representation/Fourier_Transform_Laws#Vertauschungssatz|Vertauschungssatz]] if one takes into account that the time function belonging to ${U(f)}$ is as follows (see lower sketch): | ||
| Line 21: | Line 21: | ||
''Hints:'' | ''Hints:'' | ||
| − | *This exercise belongs to the | + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Transform_Laws|Fourier Transform Laws]]. |
*All of these laws are illustrated with examples in the learning video [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Gesetzmäßigkeiten der Fouriertransformation]] . | *All of these laws are illustrated with examples in the learning video [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Gesetzmäßigkeiten der Fouriertransformation]] . | ||
The following relationship exists between ${x(t)}$ and ${y(t)}$ : | The following relationship exists between ${x(t)}$ and ${y(t)}$ : | ||
Revision as of 18:04, 27 January 2021
Like in Task 3.5 the spectrum ${Y(f)}$ of the signal
- $$y( t ) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f \ddot{u}r}}} \\ {{\rm{f\ddot{u} r}}} \\ {\rm{else.}} \\ \end{array}\;\begin{array}{*{20}c} { - T \le t < 0,} \\ {0 < t \le T,} \\ {} \\\end{array}$$
can be determined. Again, $A = 1 \,\text{V}$ and $T = 0.5 \,\text{ms}$ apply.
Assume the time signal ${x(t)}$ according to the middle sketch, which is composed of three Dirac pulses at $–T$, $0$ and $+T$ with the pulse weights ${AT}$, $-2{AT}$ und ${AT}$ .
The spectral function ${X(f)}$ can be given directly by applying the Vertauschungssatz if one takes into account that the time function belonging to ${U(f)}$ is as follows (see lower sketch):
- $$u( t ) = - 2A + 2A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$
Hints:
- This exercise belongs to the chapter Fourier Transform Laws.
- All of these laws are illustrated with examples in the learning video Gesetzmäßigkeiten der Fouriertransformation .
The following relationship exists between ${x(t)}$ and ${y(t)}$ :
- $$y( t ) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\, {\rm d}\tau .$$
- The Integration_Theorem reads in a correspondingly adapted form:
- $$\frac{1}{T}\cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\,\, {\rm d}\tau\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ X( f ) \cdot \left( {\frac{1}{{{\rm{j}}\cdot 2{\rm{\pi }\cdot }fT}} + \frac{1}{2T}\cdot {\rm \delta} ( f )} \right).$$
Questions
Solution
(1) In the description of the task you will find the Fourier correspondence between ${u(t)}$ and ${U(f)}$.
- Since both the time functions ${u(t)}$ and ${x(t)}$ and the corresponding spectra ${U(f)}$ and ${X(f)}$ are even and real, ${X(f)}$ can be easily calculated by applying the "Vertauschungssatz":
- $$X( f ) = - 2 \cdot A \cdot T + 2 \cdot A \cdot T \cdot \cos \left( {{\rm{2\pi }}fT} \right).$$
- Because of the relation $\sin^{2}(\alpha) = (1 – \cos(\alpha))/2$ it can also be written for this:
- $$X( f ) = - 4 \cdot A \cdot T \cdot \sin ^2 ( {{\rm{\pi }}fT} ).$$
- At frequency $f = 0$ ${x(t)}$ has no spectral components ⇒ ${X(f = 0)} \;\underline{= 0}$.
- For $f = 1 \,\text{kHz}$ – also $f \cdot T = 0.5$ – on the other hand:
- $$X( f = 1\;{\rm{kHz}} ) = - 4 \cdot A \cdot T = -2 \cdot 10^{ - 3} \;{\rm{V/Hz}}\; \Rightarrow \; |X( {f = 1\;{\rm{kHz}}} )| \hspace{0.15 cm}\underline{= 2 \;{\rm{mV/Hz}}}{\rm{.}}$$
(2) The spectrum ${Y(f)}$ can be determined from ${X(f)}$ by applying the integration theorem.
- Because of ${X(f = 0)} = 0$ the Dirac function does not have to be taken into account at the frequency $f = 0$ and one obtains:
- $$Y( f ) = \frac{X( f )}{{{\rm{j}} \cdot 2{\rm{\pi }}fT}} = \frac{{ - 4 \cdot A \cdot T \cdot \sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{j}}\cdot 2{\rm{\pi }}fT}} = 2{\rm{j}} \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$
- Of course, the result is the same as in Task 3.5:
- At frequency $f = 0$ ${y(t)}$ also has no spectral components ⇒ ${Y(f = 0)} \;\underline{= 0}$.
- For $f = 1\,\text{kHz} \ \ (f \cdot T = 0.5)$ one obtains a value smaller by a factor $\pi$ compared to $X(f)$ :
- $$|Y( {f = 1\;{\rm{kHz}}} )| = \frac{4 \cdot A \cdot T}{\rm{\pi }} \hspace{0.15 cm}\underline{= {\rm{0}}{\rm{.636}} \;{\rm{mV/Hz}}}{\rm{.}}$$