Aufgaben:Exercise 1.4Z: On the Doppler Effect

• Return to book

Directions of movement  $\rm (A)$, ...

The Doppler effect is the change in the perceived frequency of waves of any kind as the source (transmitter) and observer (receiver) move relative to each other.

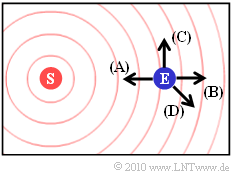
Here we always assume a static transmitter, while the receiver can move in four different directions  $\rm (A)$,  $\rm (B)$,  $\rm (C)$  and  $\rm (D)$  (see diagram).

Different speeds are to be investigated:

• an unrealistically high speed  $v_1 = 0.6 \cdot c = 1.8 \cdot 10^8 \ {\rm m/s}$,
• the maximum speed  $v_2 = 3 \ {\rm km/s} \ (10800 \ {\rm km/h})$  during unmanned test flight,
• approximately the maximum speed  $v_3 = 30 \ {\rm m/s} = 108 \ \ \rm km/h$  on federal roads.

The equations given in the theoretical section for the reception frequency are

• taking into account the theory of relativity (briefly referred to as „relativistic”):

$${\rm equation \hspace{0.15cm}(1):}\hspace{0.2cm}f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2}}{1 - v/c \cdot \cos(\alpha)} \hspace{0.05cm},$$

• without consideration of relativistic properties (referred to as „conventional”):

$${\rm equation \hspace{0.15cm}(2):}\hspace{0.2cm}f_{\rm E} = f_{\rm S} \cdot \big [ 1 + {v}/{c} \cdot \cos(\alpha) \big ] \hspace{0.05cm}.$$

Notes:

• This task belongs to the topic of  Statistical bindings within the Rayleigh process.
• $c = 3 \cdot 10^8 \ \ \rm m/s$  is the speed of light.
• To check your results you can use the applet  The Doppler Effect.

Questions

1

Which Doppler frequencies result for the speeds  $v_1$  and  $v_2$  in driving direction  $\rm (A)$  with equation (1)?

$v_1\text{:} \hspace{0.4cm} f_{\rm D}/f_{\rm S} \ = \ $

$v_2\text{:} \hspace{0.4cm} f_{\rm D}/f_{\rm S} \ = \ $ $\cdot \ 10^{-5}$

2

Which Doppler frequencies are obtained for the opposite driving direction  $\rm (B)$  with equation (1).

$v_1\text{:} \hspace{0.4cm} f_{\rm D}/f_{\rm S} \ = \ $

$v_1\text{:} \hspace{0.4cm} f_{\rm D}/f_{\rm S} \ = \ $ $\cdot \ 10^{-5}$

3

Which Doppler frequencies are obtained under otherwise identical conditions with equation (2)?

${\rm direction \ (A)}, \ \ v_1\text{:} \hspace{0.4cm} f_{\rm D}/f_{\rm S}\ = \ $

$\hspace{2.96cm} v_2\text{:} \hspace{0.4cm} f_{\rm D}/f_{\rm S}\ = \ $ $\cdot \ 10^{\rm –5}$

${\rm direction \ (B)}, \ \ v_1\text{:} \hspace{0.4cm} f_{\rm D}/f_{\rm S}\ = \ $

$\hspace{2.96cm} v_2\text{:} \hspace{0.4cm} f_{\rm D}/f_{\rm S}\ = \ $ $\cdot \ 10^{\rm –5}$

4

Let $f_{\rm S} = 2 \ \rm GHz$.  Which Doppler frequencies result for the driving direction  $\rm (C)$  and  $\rm (D)$  with  equation (2)?

${\rm direction \ (C)}, \ \ v_3\text{:} \hspace{0.4cm} f_{\rm D} \ = \ $ $\ \ \rm Hz$

${\rm direction \ (D)}, \ \ v_3\text{:} \hspace{0.4cm} f_{\rm D} \ = \ $ $\ \ \ \rm Hz$

Solution

Solution

(1)  With the driving direction  $\rm (A)$, the receiver approaches the transmitter at an angle  $\alpha = 0$.  This gives (1) according to the relativistic equation:

$$f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2}}{1 - v/c } \hspace{0.3cm} \Rightarrow \hspace{0.3cm} f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm S} \cdot \left [ \frac{\sqrt{1 - (v/c)^2}}{1 - v/c } - 1 \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{f_{\rm D}}/{f_{\rm S}} = \frac{\sqrt{1 - (v/c)^2}}{1 - v/c } - 1 \hspace{0.05cm}.$$

• With  $v_1/c = 0.6$  you get

$${f_{\rm D}}/{f_{\rm S}} = \frac{\sqrt{1 - 0.6^2}}{1 - 0.6 } - 1 = \frac{0.8}{0.4 } - 1 \hspace{0.15cm} \underline{ = 1} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E}}/{f_{\rm S}} = 2 \hspace{0.05cm}.$$

• Correspondingly with  $v_2/c = 10^{\rm -5}$:

$${f_{\rm D}}/{f_{\rm S}} = \frac{\sqrt{1 - (10^{-5})^2}}{1 - (10^{-5}) } - 1 \approx 1 + 10^{-5} - 1 \hspace{0.15cm} \underline{ = 10^{-5}} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E}}/{f_{\rm S}} = 1.00001 \hspace{0.05cm}.$$

(2)  Now the receiver moves away from the transmitter  $(\alpha = 180^°)$.

• The reception frequency  $f_{\rm E}$  is lower than the transmission frequency  $f_{\rm S}$  and the Doppler frequency  $f_{\rm D}$  is negative.  With  ${\rm cos}(\alpha) = \ -1$  you now get

$${f_{\rm D}}/{f_{\rm S}} = \frac{\sqrt{1 - (v/c)^2}}{1 + v/c } - 1 = \left\{ \begin{array}{c} \hspace{0.15cm} \underline{ -0.5} \\ \\ \hspace{0.15cm} \underline{ -10^{-5}} \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.2cm}{\rm f\ddot{u}r}\hspace{0.15cm} v_1/c = 0.6 \\ \\ {\rm f\ddot{u}r}\hspace{0.15cm} v_2/c = 10^{-5} \\ \end{array} \hspace{0.05cm}.$$

• Converting to  $f_{\rm E}/f_{\rm S}$  results in:

$${f_{\rm E}}/{f_{\rm S}} = \left\{ \begin{array}{c} \hspace{0.15cm} { 0.5} \\ \\ \hspace{0.15cm} { 0.99999} \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.2cm}{\rm f\ddot{u}r}\hspace{0.15cm} v_1/c = 0.6 \\ \\ {\rm f\ddot{u}r}\hspace{0.15cm} v_2/c = 10^{-5} \\ \end{array} \hspace{0.05cm}.$$

(3)  The following equations apply here:

$$f_{\rm E} = f_{\rm S} \cdot \left [ 1 + {v}/{c} \cdot \cos(\alpha) \right ] \Rightarrow \hspace{0.3cm}{f_{\rm D}}/{f_{\rm S}} = {v}/{c} \cdot \cos(\alpha) \hspace{0.05cm}.$$

This results in the following numerical values:

• Direction  $\rm (A)$,  $v_1 = 1.8 \cdot 10^8 \ {\rm m/s}\text{:}\hspace{0.4cm} f_{\rm D}/f_{\rm S} \ \underline {= \ 0.6} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 1.6,$
• Direction  $\rm (A)$,  $v_2 = 3.0 \cdot 10^3 \ {\rm m/s}\text{:}\hspace{0.4cm} f_{\rm D}/f_{\rm S} \ \underline {= \ 10^{\rm –5}} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 1.00001,$
• Direction  $\rm (B)$,  $v_1 = 1.8 \cdot 10^8 \ {\rm m/s}\text{:}\hspace{0.4cm} f_{\rm D}/f_{\rm S} \ \underline {= \ –0.6} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 0.4,$
• Direction  $\rm (B)$,  $v_2 = 3.0 \cdot 10^3 \ {\rm m/s}\text{:}\hspace{0.4cm} f_{\rm D}/f_{\rm S} \ \underline {= \ –10^{\rm –5}} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 0.99999.$

You can tell:

• For realistic speeds – including  $v \ \approx \ 10000 \ {\rm km/h}$  – the conventional equation  (2)  gives the same result as the relativistic equation  (1)  up to the accuracy of a pocket calculator.
• With the approximation, the angles  $\alpha = 0^°$  and  $\alpha = 180^\circ$  result in the same absolute value for the Doppler frequency.
• The approximations differ only in the sign.
• In the relativistic equation this symmetry is no longer present.  See subtasks (1) and (2).

(4)  Equation (2) leads here to the result:

$$f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm S} \cdot {v_3}/{c} \cdot \cos(\alpha) \hspace{0.05cm}.$$

• The driving direction  $\rm (C)$  is perpendicular  $(\alpha = 90^\circ)$  to the connection line transmitter–receiver.  In this case, no Doppler shift occurs:

$$f_{\rm D} \ \ \underline {= \ 0}.$$

• The driving direction  $\rm (D)$  is characterized by  $\alpha = \ –135^\circ$.  As a result:

$$f_{\rm D} = 2 \cdot 10^{9}\,\,{\rm Hz} \cdot \frac{30\,\,{\rm m/s}}{3 \cdot 10^{8}\,\,{\rm m/s}} \cdot \cos(-135^{\circ}) \hspace{0.15cm} \underline{ \approx -141\,\,{\rm Hz}} \hspace{0.05cm}.$$