Aufgaben:Exercise 3.7: Synchronous Demodulator

• Return to book

Die Spektralfunktionen  $R(f)$  und  $Z_{\rm E}(f)$

To reset an amplitude-modulated signal to the original frequency range, a  synchronous demodulator is often used::

• This multiplies the AM input signal  $r(t)$  with a carrier signal  $z_{\rm E}(t)$, on the receiving side, which should match the carrier signal  $z_{\rm S}(t)$ on the transmitting side with regard to both frequency   $f_{\rm T}$  and phase  $\varphi_{\rm T}$ .
• This is followed by a rectangular low-pass filter to eliminate all spectral components above the carrier frequency  $f_{\rm T}$. We call the output signal of the synchronous demodulator  $v(t)$.

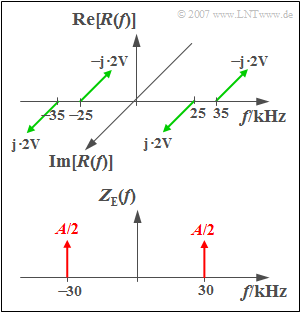
The spectrum  $R(f)$  of the received signal  $r(t)$  sketched above is produced by two-sideband amplitude modulation of a sinusoidal source signal  $q(t)$  with the frequency  $5\,\text{kHz}$  and the amplitude  $8\,\text{V}$ . A cosine signal with the frequency  $z_{\rm S}(t)$  was used as the transmission-side carrier signal  $30\,\text{kHz}$ verwendet.

The spectrum of the carrier signal  $z_{\rm E}(t)$  on the receiving side consists of two dirac lines according to the sketch below, each with the weight  $A/2$. Since  $z_{\rm E}(t)$  is not to contain a unit, the weights of the dirac functions are also dimensionless.

Hints:

• This exercise belongs to the  chapter  The Convolution Theorem and Operation.
• Important information can be found on the page  Convolution of a Function With a Dirac Function.

Questions

1

Let  $f_{\rm T} = 30\,\text{kHz}$  and  $A=1$. Calculate the output signal  $v(t)$.
What signal value occurs at time  $t = 50\, {\rm µ} \text{s}$?

$v(t = 50\, µ\text{s})\ = \ $  $\text{V}$

2

How large must the amplitude of the carrier signal  $z_{\rm E}(t)$  on the receiving side be chosen so that  $v(t) = q(t)$  is valid?

$A\ = \ $

3

Calculate the output signal  $v(t)$  under the conditions  $A = 2$  and  $f_{\rm T} = 31\,\text{kHz}$.
What signal value occurs at time  $ t = 50\, µ\text{s}$ auf?

$v(t = 50\, µ\text{s})\ = \ $  $\text{V}$

Solution

Solution

(1)  If we name the signal after the multiplier with  $m(t) = r(t) \cdot z_{\rm E}(t)$, the corresponding spectrum  $M(f)$  is the convolution product of  $R(f)$  and  $Z_{\rm E}(f)$.

• Convolution of the spectrum  $R(f)$  with the right diracline at  $+30 \text{ kHz}$  leads to discrete spectral lines at  $-\hspace{-0.08cm}5\, \text{kHz}$,  $+5 \,\text{kHz}$,  $+55 \,\text{kHz}$  and  $+65 \,\text{kHz}$. These are all imaginary and smaller than the impulse weights of  $R(f)$  by a factor of  $A/2 = 0.5$  kleiner.
• Convolution of  $R(f)$  with the Dirac at  $-\hspace{-0.08cm}30 \,\text{kHz}$  yields lines at  $-\hspace{-0.08cm}65 \,\text{kHz}$,  $-55 \,\text{kHz}$, $-5 \,\text{kHz}$  and  $+5 \,\text{kHz}$.

By superimposing the two intermediate results and taking into account the low-pass filter, which suppresses the lines at  $\pm 55 \text{ kHz}$  and  $\pm 65 \text{ kHz}$ , it thus follows for the spectrum of the descent signal:

$$V( f) = - {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f - f_{\rm N} }) + {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f + f_{\rm N} } )\hspace{0.3cm}{\rm mit}\hspace{0.3cm}f_{\rm N} = 5\;{\rm kHz}.$$

• The sink signal  $v(t)$  is therefore a  $5 \text{ kHz}$–sine signal with amplitude  $4 \text{ V}$.
• The time  $t = 50\, µ\text{s}$  corresponds to a quarter of the period  $T_0 = 1/f_{\rm N} = 200\, µ\text{s}$.
• Thus the sink signal is maximum here, i.e.  $\underline{4 \text{ V}}$.

(2)  With  $A = 1$    $v(t)$  is only half as large as  $q(t)$   ⇒   With  $\underline{A = 2}$  both signals would be equal.

(3)  The diraclines at  $\pm f_{\rm T}$  each have weight  $1$. All spectral lines mentioned below are imaginary and equal in magnitude to  $2 \text{ V}$.

• The convolution of  $R(f)$  with the right diracline of  $z_{\rm E}(t)$  yields components at  $-\hspace{-0.08cm}4\, \text{kHz (p: positiv)}$,  $+6 \,\text{kHz (n: negativ)}$, $+56 \,\text{kHz (p)}$  and  $+66 \,\text{kHz (n)}$.
• In contrast, the convolution with the left Dirac function leads to spectral lines at  $-\hspace{-0.08cm}66 \,\text{kHz (p)}$,  $-\hspace{-0.08cm}56 \,\text{kHz (n)}$,  $-\hspace{-0.08cm}6 \,\text{kHz (p)}$  und  $+4 \,\text{kHz (n)}$, all also with the (magnitude-related) impulse weights  $2 \text{ V}$.
• Taking the low pass into account, only the four spectral lines at  $\pm 4 \,\text{kHz}$  and  $\pm 6 \,\text{kHz}$.
• The associated time signal is thus with  $f_4 = 4 \,\text{kHz}$  and  $f_6 = 6 \,\text{kHz}$:

$$v( t ) = 4\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_4 t} ) + 4\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_6 t} ) \ne q( t ) = 8\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_5 t} ).$$

• At time  $t = 50\, µ\text{s}$  one obtains:

$$v( t = 50\, µ\text{s}) = 4\;{\rm{V}} \cdot \big[ {\sin \big ( {0.4{\rm{\pi }}} ) + \sin ( {0.6{\rm{\pi }}} )} \big]\hspace{0.15 cm}\underline{ = 7.608\;{\rm{V}}}{\rm{.}}$$