Aufgaben:Exercise 3.13: Path Weighting Function again

• Return to book

Zur Reduktion des Zustandsübergangsdiagramms

Auf der Seite  Regeln zur Manipulation des Zustandsübergangsdiagramms  wurde für das Beispiel unseres Rate–1/2–Standardcodes mit Gedächtnis  $m = 2$  und der Übertragungsfunktionsmatrix

$${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big )$$

die Berechnung der Pfadgewichtsfunktionen sehr ausführlich beschrieben. Als Ergebnisse wurden genannt:

$$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$

$$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$

Nun sollen die gleichen Berechnungen für den  äquivalenten systematischen Code  mit der Übertragungsfunktionsmatrix

$${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big )$$

durchgeführt werden.

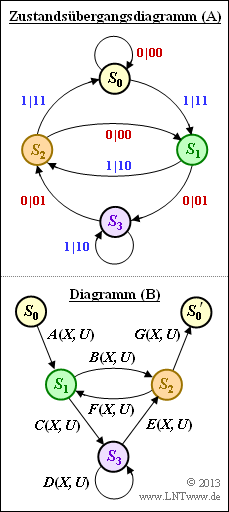
• Die Grafik zeigt das Zustandsübergangsdiagramm  $\rm (A)$  und die Struktur des reduzierten Diagramms  $\rm (B)$, wobei die Übergänge mit  $A(X, \, U), \ \text{...}\ , \ G(X, \, U)$  allgemein bezeichnet sind.
• In der Teilaufgabe (1) sollen diese Abkürzungen an das Zustandsübergangsdiagramm  $\rm (A)$  angepasst werden.

Hinweise:

• Die Aufgabegehört zum Kapitel  Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken.
• Zur Lösung der Teilaufgaben (2) und (3) verweisen wir hier nochmals auf die Seite  Regeln zur Manipulation des Zustandsübergangsdiagramms im Theorieteil.

Fragebogen

1

Für welche Ausdrücke stehen die nachfolgenden Abkürzungen?

	$A(X, \, U) = UX^2$,
	$B(X, \, U) = UX$,
	$C(X, \, U) = X$,
	$D(X, \, U) = UX$,
	$E(X, \, U) = X$,
	$F(X, \, U) = 1$,
	$G(X, \, U) = UX^2$.

2

Welche Ausdrücke gelten für die erweiterte Pfadgewichtsfunktion?

	$T_{\rm enh}(X, \, U) = UX^5 \ / \ (1 \, –2UX)$.
	$T_{\rm enh}(X, \, U) = UX^5 + 2 U^2X^6 + 4U^3X^7 + 8U^4X^8 + \ \text{...}$,
	Keiner der Vorschläge ist richtig.

3

Welche Ausdrücke gelten für die „einfache” Pfadgewichtsfunktion?

	$T(X) = X^5 \ / \ (1 \, –2X)$.
	$T(X) = X^5 + 2X^6 + 4X^7 + 8X^8 + \ \text{...} $
	Keiner der Vorschläge ist richtig.

Musterlösung

Solution

(1)  Alle Lösungsvorschläge sind richtig. Im angepassten Diagramm  $\rm (B)$  sind alle Übergänge eingezeichnet:

Zur Reduktion des Zustandsübergangsdiagramms

• Der Übergang von $S_0$ nach $S_1$ ist durch „$1 \ | \ 11$” gekennzeichnet.
• Die Ausgangssequenz $\underline{x}_i = (11)$ wird durch $X^2$ ausgedrückt, das Eingangsbit $u_i = 1$ durch $U$.
• Das gleiche Ergebnis erhält man für $G(X, \, U)$:

$$A(X, U) = G(X, U)= UX^2 \hspace{0.05cm}.$$

• Die Ausgangssequenzen $\underline{x}_i = (01)$ sowie $\underline{x}_i = (10)$ werden beide mit $X$ markiert.
• Unter Berücksichtigung der Eingangsbits erhält man somit:

$$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$

$$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X \hspace{0.05cm}.$$

• Der Übergang „$0 \ | \ 00$” von $S_2$ nach $S_1$ wird durch $F(X, \, U) = 1$ ausgedrückt.

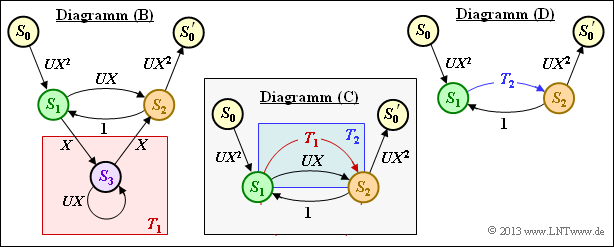
(2)  Entsprechend der Vorgehensweise auf der Seite Regeln zur Manipulation des Zustandsübergangsdiagramms im Theorieteil wird zunächst der Übergang von $S_1$ nach $S_2$ via $S_3$ durch einen Ring zusammengefasst.

• Man erhält für die rote Hinterlegung im Diagramm  $\rm (B)$:

$$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} \hspace{0.05cm}.$$

• Die beiden parallelen Übergänge entsprechend der blauen Hinterlegung im Diagramm  $\rm (C)$  können wie folgt kombiniert werden:

$$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = \frac{X^2 + U- U^2X^2}{1- U X} \hspace{0.05cm}.$$

• Die erweiterte Pfadgewichtsfunktion ergibt sich entsprechend Diagramm  $\rm (D)$  als Rückkopplung:

$$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} = \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$

Dem Autor ist es auch nach mehreren Versuchen nicht gelungen, diesen Ausdruck zielführend weiter zu vereinfachen. Er tendiert zum Lösungsvorschlag 3 mit dem Zusatz „ohne Gewähr”.

• Dieses Ergebnis würde jedoch bedeuten, dass sich die erweiterte Pfadgewichtsfunktion des äquivalenten systematischen Codes von der des nichtsystematischen Codes unterscheidet.
• Wir werden diese Frage noch mit einem Fachmann klären.

(3)  Richtig sind die Lösungsvorschläge 1 und 2:

• Setzt man in der erweiterten Funktion $T_{\rm enh}(X, \, U)$ den Formalparameter $U = 1$, so erhält man den Lösungsvorschlag 1:

$$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= \frac{X^5 }{1- X - X} = \frac{X^5 }{1- 2X} \hspace{0.05cm}.$$

• Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + \ \text{...}\ $ kommt man zum Lösungsvorschlag 2.
• Das heißt: Die einfache Pfadgewichtsfunktion $T(X)$ stimmt bei beiden Codes überein.