Aufgaben:Exercise 2.1: Rectification

• Return to book

Periodic triangular signal

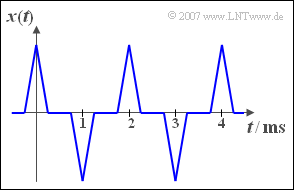
The graph shows the periodic signal  $x(t)$. If  $x(t)$ is applied to the input of a non-linearity with the characteristic curve

$$y=g(x)=\left\{ {x \; \rm for\; \it x \geq \rm 0, \atop {\rm 0 \;\;\; \rm else,}}\right.$$

the signall  $y(t)$ is obtained at the output. A second non-linear characteristic

$$z=h(x)=|x|$$

delivers the signal  $z(t)$.

Hint:

• This exercise belongs to the chapter  General description of periodic signals.

Questions

1

Which of the following statements are true?

	$y = g(x)$  describes a half-wave rectifier.
	$y = g(x)$  describes a full-wave rectifier.
	$z = h(x)$  describes a half-wave rectifier.
	$z = h(x)$  describes a full-wave rectifier.

2

What is the base frequency $f_0$  of the signal  $x(t)$?

$f_0 \ = \ $   $\text{Hz}$

3

What is the period duration  $T_0$  of the signal  $y(t)$?

$T_0 \ = \ $   $\text{ms}$

4

What is the base angular frequency  $\omega_0$  of the signal  $z(t)$?

$\omega_0 \ = \ $   $\text{1/s}$

Solution

Solution

(1)  Correct are the solutions 1 and 4:

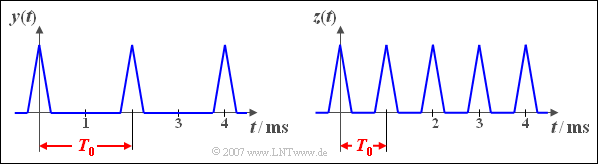
• The non-linear characteristic  $y = g(x)$  describes a half-wave rectifier.
• $z = h(x) = |x|$  describes a full-wave rectifier.

(2)  The period duration  $x(t)$  is  $T_0 = 2\,\text{ms}$. The inverse amounts to the base frequency  $f_0 \hspace{0.1cm}\underline{ = 500\,\text{Hz}}$.

(3)  The half-wave rectification does not change the duration of the period, see the left graph. Thus the following still applies  $T_0 \hspace{0.1cm}\underline{= 2\,\text{ms}}$.

Periodic triangular signals

(4)  After full-wave rectification, the signal  $z(t)$  has double the frequency (see right graph). The following values apply here:

$$T_0 = 1\,\text{ms}, \hspace{0.5cm} f_0 = 1\,\text{kHz}, \hspace{0.5cm} \omega_0 \hspace{0.1cm}\underline{= 6283\,\text{1/s}}.$$