Difference between revisions of "Aufgaben:Exercise 2.3Z: Oscillation Parameters"
From LNTwww
| Line 3: | Line 3: | ||
}} | }} | ||
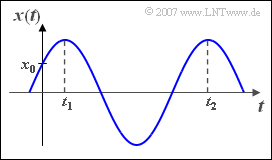
| − | [[File:P_ID316__Sig_Z_2_3.png|right|frame| | + | [[File:P_ID316__Sig_Z_2_3.png|right|frame|Definitions of $x_0$, $t_1$ und $t_2$]] |
Every harmonic oscillation can also be written in the form | Every harmonic oscillation can also be written in the form | ||
:$$x(t)=C\cdot\cos\bigg(2\pi \cdot \frac{t-\tau}{T_0}\bigg).$$ | :$$x(t)=C\cdot\cos\bigg(2\pi \cdot \frac{t-\tau}{T_0}\bigg).$$ | ||
| Line 10: | Line 10: | ||
:* the amplitude $C$, | :* the amplitude $C$, | ||
| − | :* the period duration $T_0$, | + | :* the period duration $T_0$, |
:* the shift $\tau$ with respect to a cosine signal. | :* the shift $\tau$ with respect to a cosine signal. | ||
| − | A second form of representation is with the | + | A second form of representation is with the basic frequency $f_0$ and the phase $\varphi$: |
:$$x(t)=C \cdot\cos(2\pi f_0t-\varphi).$$ | :$$x(t)=C \cdot\cos(2\pi f_0t-\varphi).$$ | ||
From a harmonic oscillation it is now known that | From a harmonic oscillation it is now known that | ||
| − | :* the first signal maximum occurs at $t_1 = 2 \,\text{ms}$ | + | :* the first signal maximum occurs at $t_1 = 2 \,\text{ms}$, |
| − | :* the second signal maximum occurs at $t_2 = 14 \,\text{ms}$ | + | :* the second signal maximum occurs at $t_2 = 14 \,\text{ms}$, |
| − | :* the value $x_0 ={x(t = 0)} = 3 \,\text{V}$ | + | :* the value $x_0 ={x(t = 0)} = 3 \,\text{V}$. |
| Line 48: | Line 48: | ||
|type="{}"} | |type="{}"} | ||
$\tau\hspace{0.25cm} = \ $ { 2 3% } $\text{ms}$ | $\tau\hspace{0.25cm} = \ $ { 2 3% } $\text{ms}$ | ||
| − | $\varphi\hspace{0.2cm} = \ $ { 60 3% } $\text{ | + | $\varphi\hspace{0.2cm} = \ $ { 60 3% } $\text{degree}$ |
| − | {What is the amplitude of the harmonic oscillation | + | {What is the amplitude of the harmonic oscillation? |
|type="{}"} | |type="{}"} | ||
${C}\ = \ $ { 6 3% } $\text{V}$ | ${C}\ = \ $ { 6 3% } $\text{V}$ | ||
Revision as of 15:27, 13 April 2021
Every harmonic oscillation can also be written in the form
- $$x(t)=C\cdot\cos\bigg(2\pi \cdot \frac{t-\tau}{T_0}\bigg).$$
The oscillation is thus completely determined by three parameters:
- the amplitude $C$,
- the period duration $T_0$,
- the shift $\tau$ with respect to a cosine signal.
A second form of representation is with the basic frequency $f_0$ and the phase $\varphi$:
- $$x(t)=C \cdot\cos(2\pi f_0t-\varphi).$$
From a harmonic oscillation it is now known that
- the first signal maximum occurs at $t_1 = 2 \,\text{ms}$,
- the second signal maximum occurs at $t_2 = 14 \,\text{ms}$,
- the value $x_0 ={x(t = 0)} = 3 \,\text{V}$.
Hint:
- This exercise belongs to the chapter Harmonic Oscillation.
Questions
Solution
(1) It is $T_0 = t_2 - t_1 = 12\, \text{ms}$ and $f_0 = 1/T_0 \hspace{0.15cm} \underline{\approx 83.33\, \text{Hz}}$.
(2) The shift is $\tau \hspace{0.1cm} \underline{= 2\, \text{ms}}$ and the phase is $\varphi = 2\pi \cdot \tau/T_0 = \pi/3$ corresponding to $\varphi =\hspace{0.15cm} \underline{60^{\circ}}$.
(3) From the value at timet $t = 0$ it follows for the amplitude ${C}$:
- $$x_0=x(t=0)=C\cdot\cos(-60\,^\circ)={C}/{2}=\rm 3\,V \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm}\hspace{0.15cm}\underline{\it C=\rm 6\,V}.$$
(4) The corresponding spectral function is:
- $$X(f)={C}/{2}\cdot{\rm e}^{-{\rm j}\varphi}\cdot\delta(f-f_0)+{C}/{2}\cdot{\rm e}^{{\rm j}\varphi}\cdot\delta(f+f_0).$$
- The weight of the Dirac line at $f = f_0$ (first term) is ${C}/2 \cdot {\rm e}^{–\text{j}\varphi} = 3 \,\text{V} \cdot \cos(60^\circ)- 3 \,\text{V} \cdot \sin(60^\circ)\hspace{0.05cm}\approx \underline{1.5 \,\text{V} - \text{j} \cdot 2.6 \,\text{V}}$.