Difference between revisions of "Aufgaben:Exercise 3.3Z: Rectangular Pulse and Dirac Delta"
From LNTwww
m (Guenter moved page Exercise 3.3Z: Rectangular- and Dirac Pulse to Exercise 3.3Z: Rectangular Pulse and Dirac Impulse) |
|||
| Line 4: | Line 4: | ||
[[File:P_ID507__Sig_Z_3_3.png|right|frame|Verschiedene Rechteckimpulse]] | [[File:P_ID507__Sig_Z_3_3.png|right|frame|Verschiedene Rechteckimpulse]] | ||
| − | We consider here a multitude of symmetrical rectangular functions $x_k(t)$. The individual rectangles differ in amplitudes (heights) | + | We consider here a multitude of symmetrical rectangular functions $x_k(t)$. The individual rectangles differ in amplitudes (heights) |
:$$A_k = k \cdot A$$ | :$$A_k = k \cdot A$$ | ||
and different pulse durations (widths) | and different pulse durations (widths) | ||
| Line 21: | Line 21: | ||
''Hints:'' | ''Hints:'' | ||
| − | *This | + | *This task belongs to the chapter [[Signal_Representation/Special_Cases_of_Pulses|Special Cases of Pulses]]. |
| + | *Use one of the functions $\text{si}(x) = \sin(x)/x$ or $\text{sinc}(x) = \sin(\pi x)/(\pi x)$. | ||
| − | *You can check your results using the two interactive applets [[Applets:Impulse_und_Spektren|Impulses and Spectra]] | + | *You can check your results using the two interactive applets |
| + | ::[[Applets:Impulse_und_Spektren|Impulses and Spectra]], | ||
| + | ::[[Applets:Frequenzgang_und_Impulsantwort|Frequenzgang und Impulsantwort]]. | ||
| Line 31: | Line 34: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Which of the following statements are true regarding the spectrum $X_1(f)$ | + | {Which of the following statements are true regarding the spectrum $X_1(f)$? |
|type="[]"} | |type="[]"} | ||
+ The spectral value $X_1(f = 0)$ is equal to $10^{–3} \,\text{V/Hz}$. | + The spectral value $X_1(f = 0)$ is equal to $10^{–3} \,\text{V/Hz}$. | ||
| Line 38: | Line 41: | ||
| − | {Which of the following statements are true regarding the spectrum $X_2(f)$ | + | {Which of the following statements are true regarding the spectrum $X_2(f)$? |
|type="[]"} | |type="[]"} | ||
| − | + The spectral value $X_2(f = 0)$ | + | + The spectral value is $X_2(f = 0)$ is equal to $10^{–3} \,\text{V/Hz}$. |
- $X_2(f)$ has zeros at the interval of $2\, \text{kHz}$. | - $X_2(f)$ has zeros at the interval of $2\, \text{kHz}$. | ||
+ $X_2(f)$ has zeros at the interval of $4 \,\text{kHz}$. | + $X_2(f)$ has zeros at the interval of $4 \,\text{kHz}$. | ||
| − | {Let $k = 10$. Calculate the frequency $f_{10}$ of the first zero and the spectral value at $f = 2 \,\text{kHz}$. | + | {Let $k = 10$. Calculate the frequency $f_{10}$ of the first zero and the spectral value at $f = 2 \,\text{kHz}$. |
|type="{}"} | |type="{}"} | ||
$f_{10} \ = \ ${ 20 3% } $\text{kHz}$ | $f_{10} \ = \ ${ 20 3% } $\text{kHz}$ | ||
| Line 51: | Line 54: | ||
| − | {What is the spectral value at | + | {What is the spectral value at $f = 2 \,\text{kHz}$ in the limiting case $k \rightarrow \infty$? Interpret the result. |
|type="{}"} | |type="{}"} | ||
$X_{\infty}(f = 2 \,\text{kHz})\ = \ $ { 1 3% } $\text{mV/Hz}$ | $X_{\infty}(f = 2 \,\text{kHz})\ = \ $ { 1 3% } $\text{mV/Hz}$ | ||
Revision as of 13:03, 23 April 2021
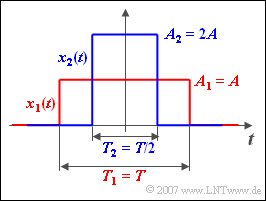
We consider here a multitude of symmetrical rectangular functions $x_k(t)$. The individual rectangles differ in amplitudes (heights)
- $$A_k = k \cdot A$$
and different pulse durations (widths)
- $$T_k = T/k.$$
Let $k$ be any positive value.
- The rectangular pulse $x_1(t)$ shown in red has the amplitude $A_1 = {A} = 2 \,\text{V}$ and the duration $T_1 = {T} = 500 \,µ\text{s}$.
- The pulse $x_2(t)$ shown in blue is half as wide ⇒ $T_2 =250 \,µ\text{s}$, but twice as high ⇒ $A_2 = 4 \text{ V}$.
Hints:
- This task belongs to the chapter Special Cases of Pulses.
- Use one of the functions $\text{si}(x) = \sin(x)/x$ or $\text{sinc}(x) = \sin(\pi x)/(\pi x)$.
- You can check your results using the two interactive applets
Questions
Solutions
(1) Proposed solutions 1 and 2 are correct:
- The spectral value at frequency $f = 0$ is always equal to the area under the time function according to the first Fourier integral :
- $$X( f ) = \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm{e}}^{ - {\rm{j2\pi }}ft} \hspace{0.1cm} {\rm d}t \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \;X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t )}\hspace{0.1cm} {\rm d}t.$$
- In the present case, the pulse area is always $A \cdot T = 10^{–3} \,\text{Vs} = 1\, \text{mV/Hz}$.
- Because of $T_1 = 500 \,µ\text{s}$ the spectrum $X_1(f)$ has zero crossings at the interval $f_1 = 1/T_1 = 2 \,\text{kHz}$ .
(2) Proposed solutions 1 and 3 are correct:
- Due to equal pulse areas, the spectral value is not changed at the frequency $f = 0$ .
- The equidistant zero crossings now occur at the interval $f_2 = 1/T_2 = 4 \,\text{kHz}$ auf.
(3) Zero crossings occur at multiples of $f_{10} = 1/T_{10} = 20 \,\text{kHz}$, and the spectral function is:
- $$X_{10} ( f ) = X_0 \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}f/f_{10} } ).$$
- At frequency $f = 2 \,\text{kHz}$ the argument of the $\rm si$-function is equal to $\pi/10$ $($or $18^{\circ})$:
- $$X_{10} ( {f = 2\;{\rm{kHz}}}) = 10^{ - 3} \;{\rm{V/Hz}} \cdot \frac{{\sin ( {18^\circ } )}}{{{\rm{\pi /10}}}} \hspace{0.15 cm}\underline{= 0.984 \;{\rm{mV/Hz}}}{\rm{.}}$$
(4) In the limiting case $k \rightarrow \infty$ the then infinitely high and infinitely narrow Rectangular impulse changes into the Dirac Delta impulse .
- Its spectrum is constant for all frequencies.
- Thus the spectral value $X_{\infty}(f = 2 \,\text{kHz})\hspace{0.15 cm}\underline{=1 \text{ mV/Hz}}$ also applies at the frequency $f = 2 \,\text{kHz}$ .