Aufgaben:Exercise 4.6Z: Locality Curve for Phase Modulation

• Return to book

A possible locus curve with phase modulation

We assume here a message signal  $q(t)$ , which is considered normalised (dimensionless).

• The maximum value of this signal is  $q_{\rm max} = 1$  and the minimum signal value is  $q_{\rm min} = -0.5$.
• Otherwise nothing is known about  $q(t)$ .

The modulated signal with phase modulation is:

$$s(t) = s_0 \cdot {\cos} ( \omega_{\rm T}\hspace{0.05cm} t + \eta \cdot q(t)).$$

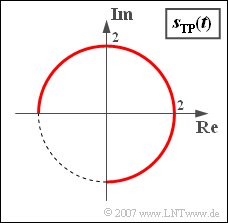
Here  $\eta$  denotes the so-called modulation index. Let the constant envelope  $s_0$  also be a dimensionless quantity, which is set to  $s_0 = 2$  in the following (see diagram).

If one replaces the cosine function with the complex exponential function, one arrives at the analytical signal

$$s_{\rm +}(t) = s_0\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}( \omega_{\rm T} \hspace{0.05cm}\cdot \hspace{0.05cm} t + \eta \hspace{0.05cm} \cdot \hspace{0.05cm} q(t)) }.$$

From this, one can calculate the equivalent low-pass signal sketched in the graph as follows:

$$s_{\rm TP}(t) = s_{\rm +}(t) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot\hspace{0.05cm} \omega_{\rm T} \hspace{0.05cm}\cdot\hspace{0.05cm} t } = s_0\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} \eta \hspace{0.05cm} \cdot \hspace{0.05cm} q(t) }.$$

Hints:

• This task belongs to the chapter  Equivalent Low-Pass Signal and Its Spectral Function.

• You can check your solution with the interactive applet  Physical Signal and Equivalent Low-Pass Signal   ⇒   locus curve,

Questions

1

What is the magnitude function  $a(t) = |s_{\rm TP}(t)|$? Which value is valid for  $t = 0$?

$a(t = 0)\ = \ $

2

Between which extreme values  $\phi_{\rm min}$  and  $\phi_{\rm max}$  does the phase  $\phi (t)$?

$\phi_{\rm min}\ = \ $  $\text{deg}$

$\phi_{\rm min}\ = \ $  $\text{deg}$

3

Determine the modulation index  $\eta$  from the phase function  $\phi (t)$.

$\eta\ = \ $

4

Which of the following statements are true?

	From  $q(t) = -0.5 = \text{const.}$  follows  $s(t) = s_0 \cdot \cos (\omega_T \cdot t)$.
	With a rectangular signal  $q(t)$  $($with only two possible signal values  $\pm 0.5)$  the locus curve degenerates to two points.
	With the signal values  $\pm 1$  $(q_{\rm min} = -0.5$  is then no longer valid$)$ the locus curve degenerates to one point:   $s_{\rm TP}(t) = -s_0$.

Solution

Solution

(1)  The locus curve is a circular arc with radius  $2$. Therefore, the magnitude function is constant  $\underline{a(t) = 2}$.

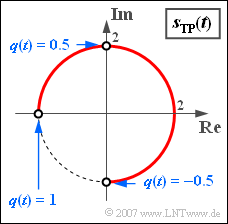
(2)  From the graph it can be seen that the following numerical values apply:

• $\phi_{\rm min} =- \pi /2 \; \Rightarrow \; \underline{-90^\circ}$,
• $\phi_{\rm max} = +\pi \; \Rightarrow \; \underline{+180^\circ}$.

(3)  In general, the relation  $s_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t)}.$ applies here. A comparison with the given function yields:

$$\phi(t) = \eta \cdot q(t).$$

• The maximum phase value  $\phi_{\rm max} = +\pi \; \Rightarrow \; {180^\circ}$  is obtained for the signal amplitude  $q_{\rm max} = 1$. From this follows directly  ${\eta = \pi} \; \underline{\approx 3.14}$.
• This modulation index is confirmed by the values  $\phi_{\rm min} = -\pi /2$  and  $q_{\rm min} = -0.5$ .

Locus curve (phase diagram) for a rectangular signal

(4)  The second and third proposed solutions are correct:

• If  $q(t) = \text{const.} =-0.5$, the phase function is also constant:

$$\phi(t) = \eta \cdot q(t) = - {\pi}/{2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{\rm TP}(t) = - {\rm j} \cdot s_0 = - 2{\rm j}.$$

• Thus, for the actual, physical signal:

$$s(t) = s_0 \cdot {\cos} ( \omega_{\rm T}\hspace{0.05cm} t - {\pi}/{2}) = 2 \cdot {\sin} ( \omega_{\rm T} \hspace{0.05cm} t ).$$

• In contrast,  $q(t) = +0.5$  leads to  $\phi (t) = \pi /2$  and to  $s_{\rm TP}(t) = 2{\rm j}$.
• If  $q(t)$  is a rectangular signal that alternates between  $+0.5$  and  $–0.5$  , then the locus curve consists of only two points on the imaginary axis, regardless of how long the intervals with   $+0.5$  and  $–0.5$ last.
• If, on the other hand,  $q(t) = \pm 1$, then the possible phase values  $+\pi$  and  $-\pi$ result purely formally, but they are identical.
• The „locus curve” then consists of only one point:   $s_{\rm TP}(t) = - s_0$  
  ⇒   the signal  $s(t)$  is „minus-cosine” for all times  $t$ .