Difference between revisions of "Aufgaben:Exercise 3.2Z: Sinc-Squared Spectrum with Diracs"
From LNTwww
m (Guenter moved page Exercise 3.2Z: Sinc-Squared-Spectrum with Diracs to Exercise 3.2Z: Sinc-Squared Spectrum with Diracs) |
|
(No difference)
| |
Latest revision as of 14:11, 24 May 2021
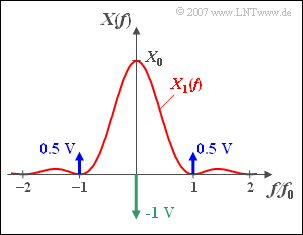
The sketched spectrum ${X(f)}$ of a time signal ${x(t)}$ is composed of
- a continuous component $X_1(f)$,
- plus three discrete spectral lines ⇒ "Dirac functions".
The continuous component with $f_0 = 200\, \text{kHz}$ and $X_0 = 10^{–5} \text{ V/Hz}$ is as follows:
- $$X_1( f ) = X_0 \cdot {\mathop{\rm sinc}\nolimits} ^2 ( {{f}/{f_0}} ),\quad {\rm where is}\quad {\mathop{\rm sinc}\nolimits} (x) = {\sin (\pi x)}/(\pi x).$$
- The spectral line at $f = 0$ has the weight $–\hspace{-0.08cm}1\,\text{V}$.
- In addition, there are two lines at frequencies $\pm f_0$, both with weight $0.5\,\text{V}$.
Hints:
- This exercise belongs to the chapter Fourier Transform and its Inverse.
- Further information on this topic can be found in the (German language) learning video Kontinuierliche und diskrete Spektren ⇒ "Continuous and discrete spectra".
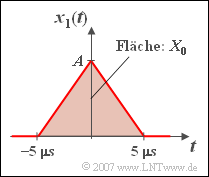
- It can be assumed as known: A triangular pulse $y(t)$ with amplitude ${A}$, the absolute duration $2T$ and symmetrical about $t = 0$ $($i.e.: the signal values are $\ne 0 $ only between $–T$ and $+T$ ) has the following spectral function:
- $$Y( f ) = A \cdot T \cdot {\rm sinc}^2 ( f T ).$$
Question
Solution
(1) The one-sided duration of the symmetrical triangular pulse is $T = 1/f_0\hspace{0.15 cm}\underline{ = 5 \,{\rm µ s}}$.
- The spectral value $X_0 = X_1(f = 0)$ indicates the pulse area of $x_1(t)$.
- This is equal to ${A} \cdot {T}$. From this follows:
- $$A = \frac{X_0 }{T} = \frac{ 10^{-5}\rm V/Hz }{5 \cdot 10^{-6}{\rm s}}\hspace{0.15 cm}\underline{= 2\;{\rm V}}.$$
(2) The DC component is given by the Dirac weight at $f = 0$. One obtains ${B} \hspace{0.15 cm}\underline{= -1 \,\text{V}}$.
(3) The two spectral lines at $\pm f_0$ together give a cosine signal with amplitude ${C} \hspace{0.15 cm}\underline{= 1 \text{V}}$.
(4) The maximum value occurs at time ${t} = 0$ (here the triangular pulse and cosine signal are maximum):
- $$x_{\text{max}} = A + B + C \hspace{0.15 cm}\underline{= +2 \text{V}}.$$
- The minimum values of ${x(t)}$ result when the triangular pulse has decayed and the cosine function delivers the value $–\hspace{-0.08 cm}1 \,\text{V}$ :
- $$x_\text{min} = {B} - {C}\hspace{0.15 cm}\underline{ = -2\, \text{V}}.$$