Dreimal Faltung

• Return to book

Impulsantwort  $h(t)$  und
drei Eingangssignale  $x(t)$

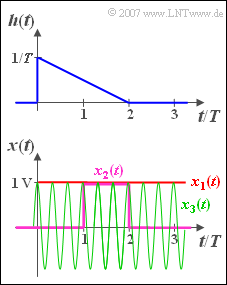
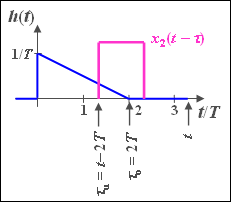
Die Impulsantwort eines LZI-Systems hat im Zeitbereich zwischen  $0$  und  $2T$  den folgenden Verlauf:

$$h( t ) = \frac{1}{T}\cdot \left( {1 - \frac{t}{ {2T}}} \right).$$

Außerhalb dieses Intervalls ist  $h(t) = 0$. Die zugehörige Spektralfunktion lautet:

$$H( f ) = \frac{1}{ {8\left( {{\rm{\pi }}fT} \right)^2 }} \cdot \left( {1 - {\rm{j \cdot 4\pi }}fT - {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 4\pi }}\hspace{0.05cm}f\hspace{0.05cm}T} } \right).$$

Zur Berechnung des so genannten "Gleichsignalübertragungsfaktors"   ⇒   $H(f = 0)$  ist diese Gleichung nicht geeignet, da sowohl der Klammerausdruck als auch der Nenner Null werden. Es gilt aber auch:

$$H( {f = 0} ) = \int_0^{2T} {h( t )\hspace{0.1cm}{\rm d}t = 1.}$$

An den Eingang dieses Filters werden drei verschiedene Zeitsignale angelegt (siehe Skizze):

• $x_1(t)$  ist ein Gleichsignal mit der Höhe  $x_0 = 1 \hspace{0.05cm}{\rm V}$.
• $x_2(t)$  ist ein Rechteckimpuls mit der Dauer  $T$  und der Höhe  $x_0 = 1\hspace{0.05cm} {\rm V}$, beginnend bei  $t = T$.
• $x_3(t)$  ist ein Cosinussignal mit der Frequenz  $f_0 = 3/T$  und der Amplitude  $x_0 = 1 \hspace{0.05cm}{\rm V}$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Faltungssatz und Faltungsoperation.
• Die Thematik dieses Abschnitts wird auch im interaktiven Applet  Zur Verdeutlichung der grafischen Faltung  veranschaulicht.

Fragebogen

1

Bei welchen der drei Signale ist es zweckmäßiger, das Ausgangssignal direkt im Zeitbereich zu berechnen?

	$y_1(t) = x_1(t) \ast h(t)$.
	$y_2(t) = x_2(t) \ast h(t)$.
	$y_3(t) = x_3(t) \ast h(t)$.

2

Wie lautet das Signal  $y_1(t)$  am Filterausgang, wenn am Eingang das Gleichsignal  $x_1(t) = 1 \hspace{0.03cm}{\rm V}$  anliegt? Geben Sie den Signalwert bei  $t = 2T$  an.

$y_1(t=2T)\ = \ $  ${\rm V}$

3

Auf welchen Zeitbereich zwischen  $t_{\text{min}}$  und  $t_{\text{max}}$  ist das Ausgangssignal  $y_2(t) = x_2(t) \ast h(t)$  beschränkt, das heißt ungleich Null?

$t_{\text{min}}/T\ = \ $

$t_{\text{max}}/T \ = \ $

4

Berechnen Sie die Werte des Signals  $y_2(t)$  zu den Zeiten  $t = 2T$  und  $t = 3T$.

$y_2(t=2T)\ = \ $  ${\rm V}$

$y_2(t=3T)\ = \ $  ${\rm V}$

5

Wie lautet das Ausgangssignal  $y_3(t)$, wenn am Eingang das Cosinussignal  $x_3(t)$  anliegt? Geben Sie den Signalwert bei  $t =0$  an.

$y_3(t=0)\ = \ $  ${\rm V}$

Musterlösung

Solution

(1)  Richtig ist die Antwort 2:

• $x_1(t)$  und  $x_3(t)$  beinhalten jeweils nur eine Frequenz, nämlich  $f = 0$  bzw.  $f = f_0$ . Hier ist jeweils der Umweg über das Spektrum vorzuziehen.
• Beim Rechtecksignal  $x_2(t)$  ist die Berechnung über die Faltung günstiger, da die Fourierrücktransformation von  $Y_2(f)$  kompliziert ist.

(2)  Beim Eingangssignal  $x_1(t)$  ist das Ausgangssignal ebenfalls ein Gleichsignal, da folgende Gleichungen gelten:

$$Y_1 (f) = X_1 (f) \cdot H(f)\quad {\rm{mit}}\quad X_1 (f) = 1\;{\rm{V}} \cdot \delta (f)$$

$$ \Rightarrow Y_1 (f) = 1\;{\rm{V}} \cdot \delta (f) \cdot H( {f = 0} ) = 1\;{\rm{V}} \cdot \delta (f) \; \Rightarrow \; y_1 (t) = 1\;{\rm{V}} \cdot H( {f = 0} ) \hspace{0.15 cm}\underline{= 1\;{\rm{V}}}.$$

• Die Berechnung über die Faltung führt zum gleichen Ergebnis, wenn man berücksichtigt, dass das Integral über die Impulsantwort im vorliegenden Fall gleich  $1$  ist.

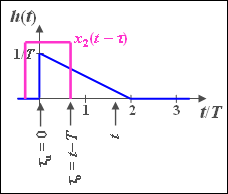
(3)  Das gespiegelte Signal  $x_2(-t)$  hat Signalanteile zwischen  $-2T$  und  $-T$.

• Erst eine Verschiebung um  $T \hspace{-0.1cm}+ \hspace{-0.1cm}\varepsilon$  führt zu einer Überlappung mit  $h(t)$. Hierbei bezeichnet  $\varepsilon$  eine beliebig kleine, aber positive Zeit.

• Ist die Verschiebung allerdings größer als  $4T\hspace{-0.1cm} - \hspace{-0.1cm}\varepsilon$, so liefert die Integration über das Produkt ebenfalls den Wert Null. Daraus folgt:

$$t_{\text{min}} \;\underline{= T}, \ \ \ t_{\text{max}} \;\underline{= 4T}.$$

Faltung Rechteck und Dreieck

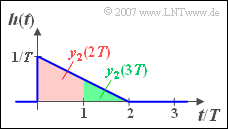
(4)  Das Ergebnis der grafischen Faltung für die Zeitpunkte  $t = 2T$  und  $t = 3T$  kann man der nebenstehenden Skizze entnehmen.

• Der Wert bei  $t = 2T$  entspricht der rötlich unterlegten Fläche:

$$y_2( {t = 2T} ) = \frac{1}{2}\cdot ( {\frac{1}{T} + \frac{1}{ {2T}}} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.75 {\rm V}} .$$

• Die grün unterlegte Fläche kennzeichnet den Wert bei  $t = 3T$:

$$y_2( {t = 3T} ) = \frac{1}{2}\cdot ( {\frac{1}{2T} + 0} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.25 {\rm V}} .$$

Um den gesamten Signalverlauf zwischen  $t = T$  und  $t = 4T$  zu berechnen, müssen drei Bereiche getrennt betrachtet werden. Zur Vereinfachung der Darstellung wird im Folgenden  $x_0 = 1$  gesetzt   ⇒   Amplitudennormierung.

Faltung für  $T \leq t \leq 2T$

(4a)  Für  $T \leq t \leq 2T$  liegt die untere Grenze bei  $τ_u = 0$, die obere Grenze bei  $τ_0 = t - T$:

$$y_2 (t) = \int_{\tau _u }^{\tau _0 } {h(\tau )\,{\rm{d}}\tau = \int_0^{t - T} {\frac{1}{T}} }\cdot \left( {1 - \frac{\tau }{ {2T}}} \right)\,{\rm{d}}\tau .$$

• Mit dem unbestimmten Integral   $I(\tau ) = {\tau }/{T} - 0.25 \cdot \left( {{\tau }/{T}} \right)^2$   ergibt sich

$$y_2 (t) = I(t - T) - I(0) = \frac{ {t - T}}{T} - 0.25 \cdot \left( {\frac{ {t - T}}{T}} \right)^2 $$

$$\Rightarrow \hspace{0.3cm}y_2 (t) = 1.5 \cdot {t}/{T} - 0.25\cdot \left( {{t}/{T}} \right)^2 - 1.25.$$

• Zur Verifizierung betrachten wir die beiden Grenzen. Man erhält die Werte  $y_2(T) = 0$  und  $y_2(2T) = 0.75$.

Faltung für  $2T \leq t \leq 3T$

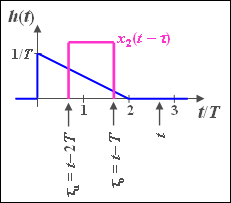
(4b)  Im Intervall  $2T \leq t \leq 3T$  gilt weiterhin  $τ_0 = t - T$, während nun  $τ_u = t - 2T$  ist:

$$y_2 (t) = I(t - T) - I(t - 2T) = 1.75 - 0.5 \cdot {t}/{T}.$$

Dies entspricht einem linearen Abfall mit den beiden Grenzwerten 

$$y_2(2T) = 0.75,$$

$$y_2(3T) = 0.25.$$

Faltung für  $3T \leq t \leq 4T$

(4c)  Für das Intervall  $3T \leq t \leq 4T$  gilt  $τ_0 = 2T$  und   $τ_u = t - 2T$:

$$y_2 (t) = I(2T) - I(t - 2T) = - 2 \cdot {t}/{T} + 0.25\left( {c{t}/{T}} \right)^2 + 4.$$

Auch hier ergeben sich die richtigen Grenzwerte:

$$y_2 (3T) = 0.25,$$

$$y_2 (4T) = 0.$$

(5)  Diese Teilaufgabe könnte prinzipiell auch direkt mit der Faltung gelöst werden.

• Da  $x_3(t)$  aber eine gerade Funktion ist, kann hier nun auf die Spiegelung verzichtet werden und man erhält:

$$y_3 (t) = \int_{ - \infty }^{ + \infty } {h(\tau ) \cdot x_3 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau = x_0 }\cdot \int_0^{2T} {h(\tau ) \cdot \cos (2{\rm{\pi }}f_0 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau .}$$

• Einfacher ist hier der Weg über die Spektren. $X(f)$  besteht aus zwei Diraclinien bei  $\pm 3f_0$. Somit muss auch nur für diese Frequenz der Frequenzgang berechnet werden:

$$H( {f = 3f_0 } ) = \frac{1}{ {72{\rm{\pi }}^{\rm{2}} }}\big[ {1 - {\rm{j}}\cdot 12{\rm{\pi }} - {\rm{cos}}( {{\rm{12\pi }}} ) + {\rm{j}}\cdot \sin ( {{\rm{12\pi }}})} \big] = \frac{1}{ {72{\rm{\pi }}^{\rm{2}} }}\big[ 1 - {\rm j}\cdot 12{\rm \pi } - 1 + {\rm j}\cdot 0 \big]= { - {\rm{j}}} \cdot \frac{1}{ {6{\rm{\pi }}}}.$$

• Somit lautet das Spektrum des Ausgangssignals:

$$Y(f) = - {\rm{j}} \cdot \frac{ {x_0 }}{{{\rm{12\pi }}}}\cdot \delta \left( {f - 3f_0 } \right) + {\rm{j}} \cdot \frac{ {x_0 }}{{{\rm{12\pi }}}}\cdot \delta \left( {f + 3f_0 } \right).$$

• Das Signal  $y_3(t)$  ist somit sinusförmig mit der Amplitude  $x_0/(6\pi )$.
• Bei  $t = 0$  ergibt sich der Signalwert  $y_3(t = 0)\; \underline{= 0}$.