Difference between revisions of "Aufgaben:Exercise 4.1Z: Appointment to Breakfast"
From LNTwww
m (Text replacement - "Category:Aufgaben zu Stochastische Signaltheorie" to "Category:Theory of Stochastic Signals: Exercises") |
m (Text replacement - "”" to """) |
||
| Line 6: | Line 6: | ||
Frau M. und Herr S. treffen sich ja bekanntlich öfter einmal zu einem gemeinsamen Frühstück: | Frau M. und Herr S. treffen sich ja bekanntlich öfter einmal zu einem gemeinsamen Frühstück: | ||
*Beide versprechen, an einem bestimmten Tag zwischen 8 Uhr und 9 Uhr zu einem solchen Treffen zu kommen. | *Beide versprechen, an einem bestimmten Tag zwischen 8 Uhr und 9 Uhr zu einem solchen Treffen zu kommen. | ||
| − | *Weiter vereinbaren sie, dass jeder von ihnen in diesem Zeitraum (und nur in diesem) auf „Gut Glück | + | *Weiter vereinbaren sie, dass jeder von ihnen in diesem Zeitraum (und nur in diesem) auf „Gut Glück" eintrifft und bis zu einer Viertelstunde auf den Anderen wartet. |
| Line 18: | Line 18: | ||
*Die Aufgabe gehört zum Kapitel [[Theory_of_Stochastic_Signals/Zweidimensionale_Zufallsgrößen|Zweidimensionale Zufallsgrößen]]. | *Die Aufgabe gehört zum Kapitel [[Theory_of_Stochastic_Signals/Zweidimensionale_Zufallsgrößen|Zweidimensionale Zufallsgrößen]]. | ||
| − | *Verwenden Sie bei den folgenden Fragen als Zeitangabe die Minute der Ankunftszeit: <br>„Minute = 0 | + | *Verwenden Sie bei den folgenden Fragen als Zeitangabe die Minute der Ankunftszeit: <br>„Minute = 0" steht für 8 Uhr, „Minute = 60" für 9 Uhr. |
*Die Aufgabe entstand vor der Bundestagswahl 2002, als sowohl Dr. Angela Merkel als auch Dr. Edmund Stoiber Kanzlerkandidat(in) der CDU/CSU werden wollten. | *Die Aufgabe entstand vor der Bundestagswahl 2002, als sowohl Dr. Angela Merkel als auch Dr. Edmund Stoiber Kanzlerkandidat(in) der CDU/CSU werden wollten. | ||
*Bei einem gemeinsamen Frühstück in Wolfratshausen verzichtete Frau Merkel. Die spätere Wahl gewann Gerhard Schröder (SPD). | *Bei einem gemeinsamen Frühstück in Wolfratshausen verzichtete Frau Merkel. Die spätere Wahl gewann Gerhard Schröder (SPD). | ||
| Line 43: | Line 43: | ||
| − | {Wie groß ist die Wahrscheinlichkeit $p_4$ für ein Zusammentreffen generell, das heißt, wenn beide tatsächlich auf „Gut Glück | + | {Wie groß ist die Wahrscheinlichkeit $p_4$ für ein Zusammentreffen generell, das heißt, wenn beide tatsächlich auf „Gut Glück" erscheinen? |
|type="{}"} | |type="{}"} | ||
$p_4 \ = \ $ { 43.75 1% } $\ \%$ | $p_4 \ = \ $ { 43.75 1% } $\ \%$ | ||
| Line 57: | Line 57: | ||
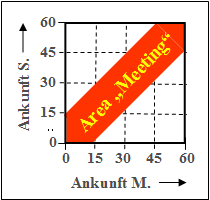
| − | [[File:EN_Sto_Z_4_1_d.png|right|frame|„Günstiger Bereich | + | [[File:EN_Sto_Z_4_1_d.png|right|frame|„Günstiger Bereich" für Zusammentreffen]] |
'''(2)''' Kommt Frau M. um 8 Uhr, so trifft sie Herrn S. nur dann, wenn dieser vor 8 Uhr 15 kommt. | '''(2)''' Kommt Frau M. um 8 Uhr, so trifft sie Herrn S. nur dann, wenn dieser vor 8 Uhr 15 kommt. | ||
*Erscheint Frau M. um 9 Uhr, dann muss Herr S. nach 8 Uhr 45 angekommen sein, damit sich beide treffen können. | *Erscheint Frau M. um 9 Uhr, dann muss Herr S. nach 8 Uhr 45 angekommen sein, damit sich beide treffen können. | ||
Revision as of 15:32, 28 May 2021
Frau M. und Herr S. treffen sich ja bekanntlich öfter einmal zu einem gemeinsamen Frühstück:
- Beide versprechen, an einem bestimmten Tag zwischen 8 Uhr und 9 Uhr zu einem solchen Treffen zu kommen.
- Weiter vereinbaren sie, dass jeder von ihnen in diesem Zeitraum (und nur in diesem) auf „Gut Glück" eintrifft und bis zu einer Viertelstunde auf den Anderen wartet.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.
- Verwenden Sie bei den folgenden Fragen als Zeitangabe die Minute der Ankunftszeit:
„Minute = 0" steht für 8 Uhr, „Minute = 60" für 9 Uhr. - Die Aufgabe entstand vor der Bundestagswahl 2002, als sowohl Dr. Angela Merkel als auch Dr. Edmund Stoiber Kanzlerkandidat(in) der CDU/CSU werden wollten.
- Bei einem gemeinsamen Frühstück in Wolfratshausen verzichtete Frau Merkel. Die spätere Wahl gewann Gerhard Schröder (SPD).
Fragebogen
Musterlösung
(1) Kommt Herr S. um 8 Uhr 30, so trifft er Frau M., wenn diese zwischen 8 Uhr 15 und 8 Uhr 45 ankommt. Damit ist die Wahrscheinlichkeit
- $$p_1 = \text{Pr(Herr S. trifft Frau M.)}\hspace{0.15cm}\underline{=50\%}.$$
(2) Kommt Frau M. um 8 Uhr, so trifft sie Herrn S. nur dann, wenn dieser vor 8 Uhr 15 kommt.
- Erscheint Frau M. um 9 Uhr, dann muss Herr S. nach 8 Uhr 45 angekommen sein, damit sich beide treffen können.
- Die Wahrscheinlichkeit für ein Zusammentreffen ist in beiden Fällen:
- $$p_2 = \big[\text{Min Pr(Herr S. trifft Frau M.)}\big]\hspace{0.15cm}\underline{=25\%}.$$
(3) Von den beiden unter (2) berechneten Ankunftszeiten ist 9 Uhr $(\underline{\text{Minute = 60}})$ günstiger,
da sie – falls Herr S. nicht da ist – sofort wieder gehen kann.
(4) Die Wahrscheinlichkeit $p_4$ ergibt sich als das Verhältnis der roten Fläche in der Grafik zur Gesamtfläche $1$.
- Mit den Dreiecksflächen erhält man:
- $$p_4=\rm 1-2\cdot\frac{1}{2}\cdot\frac{3}{4}\cdot\frac{3}{4}=\frac{7}{16}\hspace{0.15cm}\underline{=\rm 43.75\%}.$$