Aufgaben:Exercise 4.7Z: About the Water Filling Algorithm

• Return to book

Water–Filling–Prinzip  $(K = 4)$

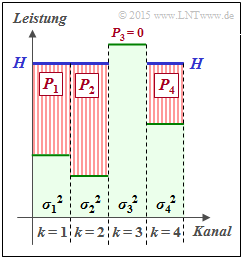
Wir betrachten  $K$  parallele Gaußsche Kanäle  (AWGN)  mit unterschiedlichen Störleistungen  $\sigma_k^2$, wobei  $1 \le k \le K$  gelten soll.  Die Grafik verdeutlicht diese Konstellation am Beispiel  $K = 4$.

Die Sendeleistung in den einzelnen Kanälen wird mit  $P_k$  bezeichnet, deren Summe den vorgegebenen Wert  $P_X$  nicht überschreiten darf:

$$P_1 +\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$

Sind die Zufallsgrößen  $X_1$, ... , $X_K$  gaußisch, so kann für die (gesamte) Transinformation zwischen dem Eingang  $X$  und dem Ausgang  $Y$  geschrieben werden:

$$I(X_1,\text{...} \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \text{...}\hspace{0.05cm}, Y_K) = 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_k}{\sigma_k^2})\hspace{0.05cm},\hspace{0.5cm} {\rm Ergebnis\hspace{0.15cm} in \hspace{0.15cm} bit} \hspace{0.05cm}.$$

Das Maximum hierfür ist die Kanalkapazität des Gesamtsystems, wobei sich die Maximierung auf die Aufteilung der Gesamtleistung  $P_X$  auf die einzelnen Kanäle bezieht:

$$C_K(P_X) = \max_{P_k\hspace{0.05cm},\hspace{0.15cm}{\rm mit} \hspace{0.15cm}P_1 + ... \hspace{0.05cm}+ P_K = P_X} \hspace{-0.5cm} I(X_1, \text{...} \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \text{...}\hspace{0.05cm}, Y_K) \hspace{0.05cm}.$$

Diese Maximierung kann mit dem Water–Filling–Algorithmus geschehen, der in obiger Grafik für  $K = 4$  dargestellt ist.

In der vorliegenden Aufgabe soll dieser Algorithmus angewendet werden, wobei von folgenden Voraussetzungen auszugehen ist:

• Zwei parallele Gaußkanäle   ⇒   $K = 2$,
• Normierte Störleistungen   $\sigma_1^2 = 1$  und  $\sigma_2^2 = 4$,
• Normierte Sendeleistungen   $P_X = 10$  bzw.  $P_X = 3$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
• Bezug genommen wird insbesondere auf die Seite  Parallele Gaußkanäle.
• Da die Ergebnisse in „bit" angegeben werden sollen, wird in den Gleichungen der Logarithmus zur Basis  $2$  verwendet:   $\log_2$.

Fragebogen

1

Welche Strategien der Leistungszuteilung sind sinnvoll?

	Einem stark gestörten Kanal  $k$  $($mit großer Störleistung  $\sigma_k^2)$  sollte eine große Nutzleistung  $P_k$  zugewiesen werden.
	Einem stark gestörten Kanal  $k$  $($mit großer Störleistung  $\sigma_k^2)$  sollte nur eine kleine Nutzleistung  $P_k$  zugewiesen werden.
	Bei gleich guten Kanälen   ⇒   $\sigma_1^2 = \text{...} = \sigma_K^2 = \sigma_N^2$  $k$  sollte die Leistung  $P_k$  gleichmäßig verteilt werden.

2

Welche Transinformation ergibt sich, wenn man die Sendeleistung  $P_X = 10$  gleichmäßig auf beide Kanäle verteilt   $(P_1= P_2 = 5)$?

$I(X_1, X_2; Y_1, Y_2) \ = \ $ $\ \rm bit$

3

Es gelte weiter  $P_X = P_1 + P_2 = 10$.  Welche optimale Leistungsaufteilung ergibt sich nach dem Water–Filling–Algorithmus?

$P_1 \ = \ $

$P_2 \ = \ $

4

Wie groß ist die Kanalkapazität für  $\underline{K = 2}$  und  $\underline{P_X = 10}$?

$C \ = \ $ $\ \rm bit$

5

Welche Transinformation ergibt sich, wenn man die Sendeleistung  $P_X = 3$  gleichmäßig auf beide Kanäle verteilt   $(P_1= P_2 = 1.5)$?

$I(X_1, X_2; Y_1, Y_2) \ = \ $ $\ \rm bit$

6

Wie groß ist die Kanalkapazität für  $\underline{K = 2}$  und  $\underline{P_X = 3}$?

$C \ = \ $ $\ \rm bit$

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 2 und 3:

• Nach den Ausführungen im Theorieteil ist „Water–Filling"   ⇒   Vorschlag 2 anzuwenden, wenn ungleiche Bedingungen vorliegen.
• Der Lösungsvorschlag 3 ist aber ebenfalls richtig:   Bei gleich guten Kanälen spricht nichts dagegen, alle  $K$  Kanäle mit gleicher Leistung   ⇒    $P_1 = P_2 =$  ...  $= P_K = P_X/K$  zu versorgen.

(2)  Für die Transinformation gilt bei gleicher Leistungsaufteilung:

$$I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{5}{4} \right )=1.292\,{\rm bit}+ 0.585\,{\rm bit} \hspace{0.15cm}\underline{= 1.877\,{\rm bit}} \hspace{0.05cm}.$$

Bestmögliche Aufteilung der Sendeleistung  $P_X = 10$

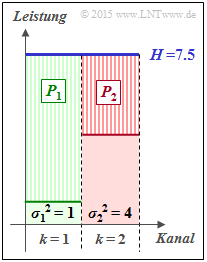
(3)  Entsprechend nebenstehender Skizze muss gelten:

$$P_2 = P_1 - (\sigma_2^2 - \sigma_1^2) = P_1 -3\hspace{0.3cm}\text{wobei }\hspace{0.3cm}P_1 + P_2 = P_X = 10$$

$$\Rightarrow \hspace{0.3cm} P_1 + (P_1 -3) = 10\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2 \cdot P_1 = 13 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{P_1 = 6.5}\hspace{0.05cm}, \hspace{0.3cm}\underline{P_2 = 3.5}\hspace{0.05cm}.$$

(4)  Die Kanalkapazität gibt die maximale Transinformation an.  Das Maximum liegt durch die bestmögliche Leistungsaufteilung gemäß der Teilaufgabe (3) bereits fest. Für  $P_X = 10$  gilt:

$$C={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{6.5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{3.5}{4} \right )$$

$$\Rightarrow\hspace{0.3cm} C=1.453\,{\rm bit}+ 0.453\,{\rm bit} \hspace{0.15cm}\underline{= 1.906\,{\rm bit}} \hspace{0.05cm}.$$

(5)  Für  $P_X = 3$  erhält man bei gleicher Leistungsaufteilung  $(P_1 = P_2 =1.5)$:

$$I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) ={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{1.5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{1.5}{4} \right ) \hspace{0.15cm}\underline{= 0.891\,{\rm bit}} \hspace{0.05cm}.$$

Bestmögliche Aufteilung der Sendeleistung  $P_X = 3$

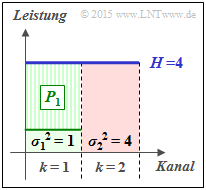
(6)  Entsprechend dem Water–Filling–Algorithmus wird die gesamte zur Verfügung stehende Sendeleistung  $P_X = 3$  nun vollständig dem ersten Kanal zugewiesen:

$${P_1 = 3}\hspace{0.05cm}, \hspace{0.3cm}{P_2 = 0}\hspace{0.05cm}.$$

• Damit erhält man für die Kanalkapazität:

$$C ={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{3}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{0}{4} \right )=1\,{\rm bit}+ 0\,{\rm bit} \hspace{0.15cm}\underline{= 1\,{\rm bit}} \hspace{0.05cm}.$$

Weitere Anmerkungen:

• Während für  $P_X = 10$  die Differenz zwischen gleichmäßiger und bester Leistungsaufteilung nur  $0.03$  bit betragen hat, ist bei  $P_X = 3$  die Differenz größer, nämlich  $0.109$  bit.
• Bei noch größerem  $P_X > 10$  wird der Unterschied zwischen gleichmäßiger und bestmöglicher Leistungsaufteilung noch geringer.

Zum Beispiel beträgt die Differenz für  $P_X = 100$  nur noch  $0.001$  bit, wie die folgende Rechnung zeigt:

• Für  $P_1 = P_2 = 50$  erhält man:

$$I = I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{50}{1} \right ) +{1}/{2}\cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{50}{4} \right )= 2.836\,{\rm bit}+ 1.877\,{\rm bit} \hspace{0.15cm}\underline{= 4.713\,{\rm bit}} \hspace{0.05cm}.$$

• Dagegen erhält man bei bestmöglicher Aufteilung   ⇒   $P_1 = 51.5, \ P_2 = 48.5$:

$$C = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{51.5}{1} \right ) +{1}/{2}\cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{48.5}{4} \right )= 2.857\,{\rm bit}+ 1.857\,{\rm bit} \hspace{0.15cm}\underline{= 4.714\,{\rm bit}} \hspace{0.05cm}.$$