Difference between revisions of "Aufgaben:Exercise 2.2Z: Average Code Word Length"
| Line 3: | Line 3: | ||
}} | }} | ||
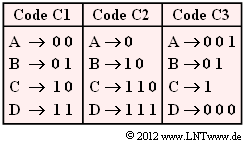
| − | [[File:P_ID2417__Inf_Z_2_2.png|right|frame| | + | [[File:P_ID2417__Inf_Z_2_2.png|right|frame|Source coding table]] |
| − | + | The aim of data compression is to represent the message of a source with as few binary characters as possible. | |
| − | + | We consider here a discrete-value message source with the symbol set $\rm \{ A, \ B, \ C, \ D\}$ ⇒ symbol range $M = 4$ and the probabilities of occurrence | |
| − | :*$p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ ( | + | :*$p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ (subtask 1), |
| − | :* $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ ( | + | :* $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ (from subtask 2). |
| − | + | It is assumed that there are no statistical ties between the individual source symbols. | |
| − | + | A measure for the quality of a compression method is the average codeword length $L_{\rm M}$ with the additional unit "bit/source symbol". | |
| − | + | Three assignments are given. To be noted: | |
| − | * | + | * Each of these binary codes $\rm C1$, $\rm C2$ and $\rm C3$ is designed for a specific source statistic. |
| − | * | + | * All codes are prefix-free and thus immediately decodable without further specification. |
| Line 26: | Line 26: | ||
| − | '' | + | ''Hint:'' |
| − | * | + | *The task belongs to the chapter [[Information_Theory/Allgemeine_Beschreibung|General description of source coding]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Determine the mean codeword length $L_{\rm M}$ for $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$. |
|type="{}"} | |type="{}"} | ||
| − | $\text{C1:}\ \ L_{\rm M} \ = \ $ { 2 1% } $\ \rm bit/ | + | $\text{C1:}\ \ L_{\rm M} \ = \ $ { 2 1% } $\ \rm bit/source symbol$ |
| − | $\text{C2:}\ \ L_{\rm M} \ = \ $ { 2.25 1% } $\ \rm bit/ | + | $\text{C2:}\ \ L_{\rm M} \ = \ $ { 2.25 1% } $\ \rm bit/source symbol$ |
| − | $\text{C3:}\ \ L_{\rm M} \ = \ $ { 2.25 1% } $\ \rm bit/ | + | $\text{C3:}\ \ L_{\rm M} \ = \ $ { 2.25 1% } $\ \rm bit/source symbol$ |
| − | { | + | {Which values result for $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$? |
|type="{}"} | |type="{}"} | ||
| − | $\text{C1:}\ \ L_{\rm M} \ = \ $ { 2 1% } $\ \rm bit/ | + | $\text{C1:}\ \ L_{\rm M} \ = \ $ { 2 1% } $\ \rm bit/source symbol$ |
| − | $\text{C2:}\ \ L_{\rm M} \ = \ $ { 1.75 1% } $\ \rm bit/ | + | $\text{C2:}\ \ L_{\rm M} \ = \ $ { 1.75 1% } $\ \rm bit/source symbol$ |
| − | $\text{C3:}\ \ L_{\rm M} \ = \ $ { 2.5 1% } $\ \rm bit/ | + | $\text{C3:}\ \ L_{\rm M} \ = \ $ { 2.5 1% } $\ \rm bit/source symbol$ |
| − | { | + | {How can you recognise prefix-free codes? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + No code word is the beginning of another code word. |
| − | - | + | - All codewords have the same length. |
| − | { | + | {For the special source symbol sequence $\rm ADBDCBCBADCA$ , the code symbol sequence $\rm 001101111001100100111000$ results. |
| − | <br> | + | <br>Which code was used? |
|type="()"} | |type="()"} | ||
| − | + | + | + the code $\rm C1$, |
| − | - | + | - the code $\rm C2$. |
| − | { | + | {After coding with $\rm C3$ , you get $\rm 001101111001100100111000$. What is the corresponding source symbol sequence? |
|type="()"} | |type="()"} | ||
- $\rm AACDBACABADAAA$ ... | - $\rm AACDBACABADAAA$ ... | ||
| Line 70: | Line 70: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The average codeword length is generally given by |
:$$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} | :$$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | If the four source symbols are equally probable $($all probabilities exactly $1/4)$, then for this we can also write: | |
:$$L_{\rm M} = 1/4 \cdot ( L_{\rm A} + L_{\rm B}+ L_{\rm C} + L_{\rm D}) | :$$L_{\rm M} = 1/4 \cdot ( L_{\rm A} + L_{\rm B}+ L_{\rm C} + L_{\rm D}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * $\text{Code C1:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.00}\ \rm bit/ | + | * $\text{Code C1:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.00}\ \rm bit/source symbol$, |
| − | * $\text{Code C2:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/ | + | * $\text{Code C2:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/source symbol$ |
| − | * $\text{Code C3:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/ | + | * $\text{Code C3:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/source symbol$. |
| − | '''(2)''' | + | '''(2)''' With the code table $\text{C1}$ , the average code word length $L_{\rm M} \hspace{0.15cm}\underline{= 2}\ \rm bit/source symbol$ is always obtained, independent of the symbol probabilities. |
| − | + | For the other two codes one obtains: | |
| − | * $\text{Code C2:}$ $L_{\rm M} = 1/2 \cdot 1 + 1/4 \cdot 2 + 1/8 \cdot 3 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 1.75}\ \rm bit/ | + | * $\text{Code C2:}$ $L_{\rm M} = 1/2 \cdot 1 + 1/4 \cdot 2 + 1/8 \cdot 3 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 1.75}\ \rm bit/source symbol$, |
| − | * $\text{Code C3:}$ $L_{\rm M} = 1/2 \cdot 3 + 1/4 \cdot 2 + 1/8 \cdot 1 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 2.50}\ \rm bit/ | + | * $\text{Code C3:}$ $L_{\rm M} = 1/2 \cdot 3 + 1/4 \cdot 2 + 1/8 \cdot 1 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 2.50}\ \rm bit/source symbol$. |
| − | + | You can see the principle from the example: | |
| − | * | + | *Probable symbols are represented by a few binary symbols, improbable ones by more. |
| − | * | + | *In the case of equally probable symbols, it is best to choose the same codeword lengths. |
| − | '''(3)''' | + | '''(3)''' <u>Solution suggestion 1</u> is correct: |
| − | * | + | *The code $\text{C1}$ with uniform length of all codewords is prefix-free, |
| − | * | + | *but other codes can also be prefix-free, for example the codes $\text{C2}$ and $\text{C3}$. |
| − | '''(4)''' | + | '''(4)''' <u>Solution suggestion 1</u> is correct: |
| − | * | + | *Already from "00" at the beginning one can see that the code $\text{C2}$ is out of the question here, because otherwise the source symbol sequence would have to begin with "AA". |
| − | * | + | *In fact, the code $\text{C1}$ was used. |
| − | '''(5)''' | + | '''(5)''' <u>Solution suggestion 2</u> is correct: |
| − | * | + | *The first suggested solution, on the other hand, gives the source symbol sequence for code $\text{C2}$ if the code symbol sequence would be $\rm 001101111001100100111000$ . |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 21:43, 2 July 2021
The aim of data compression is to represent the message of a source with as few binary characters as possible.
We consider here a discrete-value message source with the symbol set $\rm \{ A, \ B, \ C, \ D\}$ ⇒ symbol range $M = 4$ and the probabilities of occurrence
- $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ (subtask 1),
- $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ (from subtask 2).
It is assumed that there are no statistical ties between the individual source symbols.
A measure for the quality of a compression method is the average codeword length $L_{\rm M}$ with the additional unit "bit/source symbol".
Three assignments are given. To be noted:
- Each of these binary codes $\rm C1$, $\rm C2$ and $\rm C3$ is designed for a specific source statistic.
- All codes are prefix-free and thus immediately decodable without further specification.
Hint:
- The task belongs to the chapter General description of source coding.
Questions
Solution
- $$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}.$$
If the four source symbols are equally probable $($all probabilities exactly $1/4)$, then for this we can also write:
- $$L_{\rm M} = 1/4 \cdot ( L_{\rm A} + L_{\rm B}+ L_{\rm C} + L_{\rm D}) \hspace{0.05cm}.$$
- $\text{Code C1:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.00}\ \rm bit/source symbol$,
- $\text{Code C2:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/source symbol$
- $\text{Code C3:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/source symbol$.
(2) With the code table $\text{C1}$ , the average code word length $L_{\rm M} \hspace{0.15cm}\underline{= 2}\ \rm bit/source symbol$ is always obtained, independent of the symbol probabilities.
For the other two codes one obtains:
- $\text{Code C2:}$ $L_{\rm M} = 1/2 \cdot 1 + 1/4 \cdot 2 + 1/8 \cdot 3 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 1.75}\ \rm bit/source symbol$,
- $\text{Code C3:}$ $L_{\rm M} = 1/2 \cdot 3 + 1/4 \cdot 2 + 1/8 \cdot 1 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 2.50}\ \rm bit/source symbol$.
You can see the principle from the example:
- Probable symbols are represented by a few binary symbols, improbable ones by more.
- In the case of equally probable symbols, it is best to choose the same codeword lengths.
(3) Solution suggestion 1 is correct:
- The code $\text{C1}$ with uniform length of all codewords is prefix-free,
- but other codes can also be prefix-free, for example the codes $\text{C2}$ and $\text{C3}$.
(4) Solution suggestion 1 is correct:
- Already from "00" at the beginning one can see that the code $\text{C2}$ is out of the question here, because otherwise the source symbol sequence would have to begin with "AA".
- In fact, the code $\text{C1}$ was used.
(5) Solution suggestion 2 is correct:
- The first suggested solution, on the other hand, gives the source symbol sequence for code $\text{C2}$ if the code symbol sequence would be $\rm 001101111001100100111000$ .