Aufgaben:Exercise 2.3: About the LZ78 Compression

• Return to book

The LZ78–inventors

In contrast to entropy coding according to Huffman or Shannon, where one must know the source statistics (as precisely as possible), such restrictions do not apply to the compression methods developed by  Abraham Lempel  and  Jacob Ziv .  This is called universal source coding.

In this task, we consider the variant first published in 1978  [LZ78].  The string  BARBARA–BAR is to be encoded.

• The procedure LZ78 works with a global dictionary, which is initially only filled with an empty character  $(\varepsilon)$  under the index  $I = 0$ .  This distinguishes "LZ78" from its predecessor "LZ77" (with local dictionary) and also from its successor "LZW" (dictionary is prefilled with the possible characters).
• f a character or a word fragment (several characters) of the input string is found in the dictionary, the index  $I_0$  of this entry is output together with the next input character  $Z$ .  In each step  $i$  the output is therefore:   $(I_0, \ Z)$.
• Afterwards, the new string is entered into the dictionary under the next free index  $I_{\rm neu}$ .
• If one considers the dictionary as a field  $W\big[\hspace{0.05cm}I\hspace{0.05cm}\big]$  with  $I ≥ 0$, where each element contains a string of arbitrary length, then with the character variable  $Z$:

$$W \big[\hspace{0.05cm}I_{\rm neu}\hspace{0.05cm}\big] = W\big[\hspace{0.05cm}I_0\hspace{0.05cm}\big] + Z \hspace{0.05cm}. $$

For clarification, a simple example:

• At a given time, the dictionary is filled up to index  $I_{\rm akt }= 20$ .
• Handy  is waiting to be encoded.  In the dictionary, the   Ha  is found under index  $I = 11$  and the entry Han under index  $I = 16$ .
• Thus, the current code output is   $(I_0, Z) = (16,$ d$)$  and the following is entered into the dictionary as a new phrase:   $W(21) =$ Hand.
• Now the string  y  is available for coding.  If no suitable entry is found,   $(0,$ y$)$  is output and a new entry is made in the dictionary:   $W(22) = $ $\rm ε$  + y $=$ y .

For subtask  (6)  you can assume the following:

• The decimal number  $I$  (index) is represented in binary by three bits.
• The character  $Z ∈ \{$A,  B,  R,  –$ \}$  is binary coded by two bits each.

Hints:

• The task belongs to the chapter  Compression According to Lempel, Ziv and Welch.
• In particular, reference is made to the page  The Lempel-Ziv Variant LZ78 .
• The original literature  [LZ78]  on this method is:  
  Ziv, J.; Lempel, A.: Compression of Individual Sequences via Variable-Rate Coding. In: IEEE Transactions on Information Theory, no. 5, vol. 24, 1978, p. 530–536.

•   Exercise 2.3Z  and  Exercise 2.4  deal with other Lempel–Ziv methods in a similar way.

Questions

1

Which statements apply to the preassignment of the LZ78 dictionary?

	Only the index  $I = 0$  with the space  $(\varepsilon)$ is preassigned.
	The indices  $I = 0$  to  $I = 3$  with the four characters  A,  B,  R  and  – are preallocated.

2

What happens in the coding step  $i = 1$?

	The coder output is:   $(0,$ B$)$.
	The dictionary entry is:   $W(I = 1) =$ B.
	The dictionary entry is:   $W(I = 1) =$ BA.

3

Which statements are true for the coding steps  $i = 2$  and  $i = 3$?

	For  $i = 2$ , the following is true:   Output  $(0,$ A$)$,   entry  $W(I = 2) =$ A.
	For  $i = 3$ , the following is true:   Output  $(0,$ R$)$,   entry  $W(I = 3) =$ R.

4

Which statements are true for the coding step  $i = 4$?

	At step  $i = 4$    BAR  is coded together.
	At step  $i = 4$    BA  is coded together.
	The coder output is:   $(2,$ AR$)$.
	The coder output is:   $(1,$ A$)$.

5

Complete the LZ78 coding.  After which coding step  $i_{\rm Ende}$  is  BARBARA–BAR  completely coded?

$i_{\rm Ende} \ = \ $

6

How many binary characters are needed to code  BARBARA–BAR ?  Follow the instructions on the information page.

$\text{without coding: }\ N \ = \ $ $\ \rm Bit$

$\text{with LZ78 coding: }\ N \ = \ $ $\ \rm Bit$

Solution

Solution

(1)  Statement 1 applies to the LZ78 algorithm:

• In contrast, the preassignment according to statement 2 is true for the LZW algorithm, which was published in 1983 together with Terry Welch.

(2)  $\rm ε$  denotes the empty character. 

• Since  $\rm ε$ + B = B ,statements 1 and 2 are correct.
• Statement 3 is again only true for LZW compression.

(3)  Here both statements are true.

(4)&nbsp Statements 2 and 4 are correct:

• In the dictionary, character  B  is found under index   $I = 1$ .
• The next character  A  of the input sequence is appended:   (1, A).
• Statement 3 cannot be correct because  $Z$  can only be a character and not a character sequence.

LZ78 coding of  BARBARA–BAR

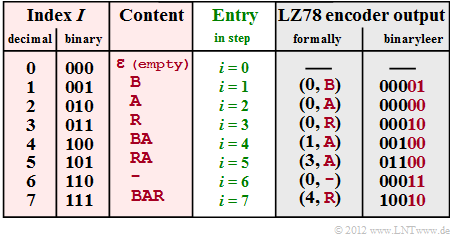
(5)  The entire coding process is summarised in a table. One can see:

• At each time  $i$ , the edited string is entered into the dictionary.
• At time  $\underline{i=7}$  the coding process is completed.

(6)  If we represent all indices with three bits and the four characters with two bits each, we get the following results:

• without coding:   $N = 11 \cdot 2 \hspace{0.15cm}\underline {= 22 \, \rm Bit}$,
• with LZ78 coding:   $N = 7 \cdot (3+2) \hspace{0.15cm}\underline {= 35 \, \rm Bit}$.

You can see from this:

• Any LZ compression only makes sense with a larger file, even if one believes that a text like  BARBARA–BAR  accommodates the LZ78 algorithm.
• With variable number of bits for the index according to task 2.4, the result for this LZ78 example would be:

$$N = 1 \cdot 3 + 2 \cdot 4 + 4 \cdot 5 = 31 \,{\rm Bit}\hspace{0.05cm}.$$